Вопрос46. Выпуклость и вогнутость функции. Точки перегиба. Асимптоты.

График функции y=f(x) называется выпуклым в интервале (a,b), если он расположен ниже касательной, проведенной в любой точке этого интервала.

График функции y=f(x) называется вогнутым в интервале (a,b), если он расположен выше касательной, проведенной в любой точке этого интервала.

Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба.

Достаточное условие выпуклости графика функции: Если во всех точках интервала (a,b) _f” (x)<0, то кривая y=f(x)в этом интервале выпукла.

Достаточное условие вогнутости графика функции: Если во всех точках интервала (a,b) _f” (x)>0, то кривая y=f(x)в этом интервале вогнута.

Достаточный признак точки перегиба: Если в точке x_{0 функция} f(x) имеет производную f’(x₀), а вторая производная _f” (x₀) в этой точке равна нулю или не существует и, кроме того, при переходе через x₀ меняет знак, то (x_0; f(x₀))- точки перегиба графика функции

Асимптоты:

1)Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий 

,

2)Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если  (x→±∞)

3)Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если  (x→±∞)

Вопрос 47. Общая схема исследования функции и построение её графика.

1) Найти область определения(D).

2)Е: Множество значений.

3) Четность, нечетность, периодичность.

4)Интервалы непрерывности, точки разрыва

5) Исследовать поведение функции в окрестности точек разрыва.

6) Найти нули функции(т.е.точки пересечения графика с осями координат)

7)Найти интервалы монотонности функции, точки экстремума(max,min)

8) Найти Интервалы выпуклости, вогнутости графика функций и точки перегиба.

9)Найти асимптоты графика функции

10)Составить свободную таблицу исследования.

11)Построить график функции.

Вопрос 49. Первообразная функция. Неопределенный интеграл. Основные свойства неопределенного интеграла.

Функция F(x) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке этого промежутка выполняется условие F’(x)=f(x) производная от первообразной равна самой функции.

 Совокупность всех пepвoобpaзныx для функции ƒ(х) на промежутке X,называется неопределенным интегралом от функции ƒ(х) .

∫ƒ(x)dx= F(x)+C.

Здесь ƒ(х) называется подынтегральнoй функцией, ƒ(x)dx —   подынтегральным выражением, х - переменной интегрирования, ∫ - знаком неопределенного интеграла.

Операция нахождения неопределенного интеграла от функции называется интегрированием  этой функции.

Свойства неопределенного интеграла

1) (∫ƒ(x)dx)^'=ƒ(х).

2) d(∫ƒ(x)dx)=ƒ(x)dх

3) ∫dF(x)= F(x)+C.

4)

5)

6) Если   , где u=φ(х) - произвольная функция, имеющая непрерывную производную.

Вопрос51. Метод непосредственного интегрирования.

Метод интегрирования, при котором данный интеграл путем тождественных пpeобpaзoвaний подынтегральной фyнкции (или выражения) и применения свойств нeoпpеделeннoгo интеграла приводится к oдиoмy или нескольким табличным интегралам, называется нeпоcpeдcтвeнным uнmeгpирoванием.

При сведении даннoгo интеграла к табличному часто используются следующие пpeoбpазoвания диффeренциaлa (операция «подвeдeния под знак дuффepeнциала»):

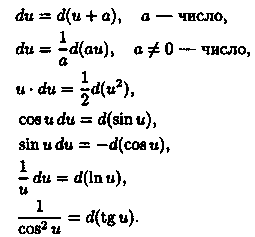
Boобщe, ƒ'(u)du=d(ƒ(u)), эта формула очень частo используется при вычислении интегралов.