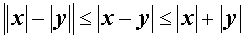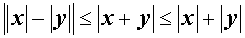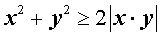- •1 Вопрос: Множество и его элементы. Подмножества. Основные операции над множествами. Действительные числа и числовая ось. Абсолютная величина действительного числа и ее свойства.
- •Числовая ось
- •Вопрос 2: Метод координат. Направленные отрезки и их величины. Основное тождество. Координаты на прямой. Прямоугольная система координат на плоскости.
- •Вопрос 3: Простейшие задачи аналитической геометрии на плоскости – расстояние между двумя точками, площадь треугольника, деление отрезка в данном отношении.
- •Вопрос4: Полярные координаты. Связь между прямоугольными и полярными координатами.
- •Вопрос 5: Преобразования прямоугольных координат – параллельный сдвиг осей, поворот осей координат.
- •Неполные уравнения плоскости
- •Вопрос 7: Уравнение прямой с угловым коэффициентом; уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Вопрос 8: Уравнение прямой проходящей через 2 данные точки; уравнение прямой в «отрезках».
- •Вопрос 9: Взаимное расположение двух прямых на плоскости. Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.
- •Вопрос 10: Эллипс, его свойства и график. Эксцентриситет эллипса.
- •Вопрос 11: Гипербола, её свойства и график. Асимптоты и эксцентриситет гиперболы.
- •Вопрос 12: Парабола. Её свойства и график.
- •Вопрос 13: Общее уравнение линии второго порядка и его приведение к простейшему виду. Классификация линий второго порядка.
- •Приведение уравнения линии второго порядка к простейшему виду
- •Классификация линий второго порядка
- •Вопрос 14: Постоянные переменные величины. Определение функции. Способы задания функций. Четные и нечетные, периодические, монотонные функции.
- •Четные и нечетные функции
- •Монотонные функции
- •Вопрос 15: Основные элементарные функции – линейная, степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции функции и их свойства.
- •Вопрос 16: Понятие неявной функции. Сложная и обратная функции. Понятие неявной функции
- •Сложная функция
- •Понятие обратной функции
- •Вопрос 19.Бесконечно большие и бесконечно малые последовательности. Основные свойства б.М. Последовательностей.
- •Вопрос 20: Сходимость числовых последовательностей. Основные свойства сходящихся последовательностей. Предельный переход в неравенства.
- •Сходящиеся последовательности
- •Предельный переход в неравенствах
- •Вопрос 22: Предел функции. Определение предела функции в точке. Предел функции при х→∞. Односторонние пределы.
- •Вопрос 23: Основные теоремы о пределах: единственность предела функции, пределы функций f(X) g(X), f(X)·g(X), f(X)/g(X), c·f(X).
- •Вопрос 24: Бесконечно малые и бесконечно большие функции. Аривметические операции над бесконечно малыми функциями.
- •Вопрос 25: Два замечательных предела.
- •Вопрос 26:Приращение аргумента и функции. Определение непрерывности функции в точке.
- •Вопрос 28: Свойства функций непрерывных в точке. Непрерывность функций f(X) g(X), f(X)·g(X), f(X)/g(X).
- •Вопрос 29: Теорема о непрерывности сложной и обратной функций.
- •Непрерывность сложной функции
- •Вопрос 30: Точки разрыва функции и их классификация.
- •Вопрос 31: Производная. Задача о наклоне касательной к кривой. Задача о производительности труда. Общее определение производной. Геометрический и экономический смысл производной.
- •Вопрос32. Производная суммы, произведения, частного.
- •Вопрос 33: Производные тригонометрических функций
- •Вопрос 34: Производные логарифмической, обратной и показательной функций.
- •Вопрос 35:Производные обратных тригонометрических функций.
- •Вопрос 36. Производная сложной функции. Производная неявной функции.
- •Вопрос 37: Логарифмическая производная.
- •Вопрос 39: Понятие дифференциала. Геометрический смысл дифференциала. Свойства дифференциала.
- •Вопрос 40: Применение дифференциала в приближенных вычислениях. Абсолютная и относительная погрешность числа.
- •Применение дифференциала в приближенных вычислениях
- •Вопрос 44.Экстремум функции. Признаки постоянства, возрастания и убывания функции.
- •Вопрос 45. Необходимое условие экстремума, критические точки. Достаточные признаки существования экстремума функции. Наибольшее и наименьшее значение функции.
- •Вопрос46. Выпуклость и вогнутость функции. Точки перегиба. Асимптоты.
- •Вопрос 47. Общая схема исследования функции и построение её графика.
- •Вопрос 49. Первообразная функция. Неопределенный интеграл. Основные свойства неопределенного интеграла.
- •Вопрос51. Метод непосредственного интегрирования.
- •Вопрос 52.Метод замены переменной.
- •Вопрос53.Метод интегрирования по частям.
- •Вопрос54.Интегрирование дробно-рациональных функций.
- •Вопрос 59.Определенный интеграл как предел интегральный суммы. Геометрический и физический смысл определенного интеграла.
- •Вопрос 60.Формула Ньютона-Лейбница .
- •Вопрос 61. Интегрирование заменой переменной.
- •Вопрос 62 Интегрирование по частям определенного интеграла.
- •Вопрос 63. Несобственные интегралы с бесконечными пределами интегрирования.
- •Вопрос 64. Несобственные интегралы от неограниченных функций
- •Вопрос 65.Вычисление площадей плоских фигур
- •Вопрос 66. Вычисление длины дуги плоской кривой
- •Вопрос 67. Вычисление объема тела.
- •Вопрос 69.Числовые ряды. Сходящиеся и расходящиеся ряды. Необходимый признак сходимости.
- •Вопрос 70. Достаточные признаки сходимости рядов.
- •Вопрос 71. Абсолютная и условная сходимость знакопеременного ряда.
1 Вопрос: Множество и его элементы. Подмножества. Основные операции над множествами. Действительные числа и числовая ось. Абсолютная величина действительного числа и ее свойства.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются буквами лат. алфавита (А, В, С), а их элементами малыми буквами (а, b с), (аСА).
Замечание: Множества, не содержащие ни одного элемента, называются пустыми.
Два множества называются равными, если они состоят из одних и тех же элементов.
Конечное множество можно создать списком элементов, при этом элементы множества записываются в фигурных скобках А={1,2,3}.
Подмножества:
Множество А называется подмножеством В, если каждый элемент подмножества А является множеством В (АсВ).
А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn
N={1,2,...,n} — множество натуральных чисел
Z={0,±1,±2,...,±n} — множество целых чисел
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
АUВ={ } Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
А∩В={ } Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
А/В={ } Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Действительные числа и числовая ось.
R – действительные числа
Множества действительных чисел содержит рациональные и иррациональные числа.
Всякое иррациональное число может быть представлено или конечной десятичной дробью или бесконечной периодической десятичной дробью.
Действительные числа, не являющиеся рациональными, называются иррациональными числами.
2/5=0,4 – рациональное число
√2 – иррациональное число.
Числовая ось
Прямая, на которой указано направление, начало отчёта, масштаб, называется числовой прямой. Числовая ось задаёт взаимно однозначное соответствие между действительными числами и точками числовой оси. Число, определяющие положение точки на числовой оси, называют координатой точки на этой оси. Координата точки на прямой определяется:
расстоянием её от начала отсчёта "О" в соответствии с выбранным масштабом;
знаком в соответствии с выбранным направлением на оси: если точка находится правее начала отсчёта "О", то координата принимается со знаком "+"; если точка находится левее начала отсчёта "О", то координата принимается со знаком "-".
Числовыми промежутками называются подмножества действительных чисел.
Опр: Окрестностью точки Хо называется любой интервал а, b.
(Хо-ε; Хо+ε), ε>0
Ε – окрестность точки Хо.
Опр: Модулем действительного числа Х называется неотрицательное число, обозначаемое |х| и определенное равенствами:
![]()
Замечание: Геометрическое число абсолютной величины числа х, есть расстояние от точки Х до начала отсчета.
Свойства модуля
Если
![]() и
и
![]() –
действительные числа, то справедливы
равенства:
–
действительные числа, то справедливы
равенства:
|
|
|
|
|
|
Кроме того, справедливо соотношение:
![]()
В то же время справедливы неравенства:
-
 (неравенство
треугольника)
(неравенство
треугольника)