11. Матрица. Квадратная, треугольная и диагональная матрицы

Матрицей размера m×n называют прямоугольную числовую таблицу, состоящую из mn чисел, которые расположены в m строках и n столбцах.

Квадратная матрица – матрица, число строк и столбцов которой равны. n=m

Треугольная матрица – матрица, все элементы над главной диагональю равные 0.

Диагональная матрица – все элементы, расположенные вне главной диагонали, равны 0.

Умножение матрицы на вектор. Свойства.

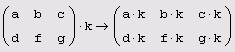
Операция определена, когда число столбцов матрицы равно числу координат вектора.

A_n * B_{n k} = C_k

A(m*n) k=(k1,k2,…,k3)

Ak=k1(a11) + k2(a12) + … +kn(a1m)

a21 a22 a2m

…. …. …..

an1 an2 anm

Свойства умножения матрицы на вектор:

1) A(K+L)=AK+AL (K,L- вектора, A- матрица)

2) A(lK)=l(AK) (l-число)

Умножение вектора на матрицу:

Операция определена,когда координат вектора столько,сколько строк у матрицы.

1 2 3

*

1 3 0 7 4 5

=

13 32

, т.е. 1*1 + 2*0 + 3*4 = 1+0+12 = 13,  1*3 + 2*7 + 3*5 = 3+14+15 = 32.

Свойства:

1. (K+L)A=KA+LA; K,L-векторы, A-матрица

2. (kL)A=k(LA); k-число

3. (LA)K=L(AK); K,L-векторы

12. Умножение матрицы на число и сложение матриц. Свойства

1. Умножение матрицы на число – каждый элементы матрицы умножается на число

2. Сложение матриц – складываются матрицы только одинаковой размерности. Складываются элементы стоящие на одинаковых местах.

Свойства:

1. A+B=B+A A,B,C - матрицы

2. (A+B)+C=A+(B+C) k,l - числа

3. A(k+l)=Ak+Al

4. A(kl)=(Ak)l=k(Al)

5. (A+B)k=Ak+Bk

13. Умножение матриц. Вычисление строк и столбцов полученной матрицы. Свойства

AxB: произведение определено, если число столбцов A равняется числу строк B.

A (m*n), B(k*l), n=k => C(m*l)

В общем случае произведение матриц непомутативно (множители нельзя переставлять местами)

(AB)_j=A*B_j (столбец)

(AB)i=Ai(наверху)*B(строка)

Свойства:

1. (AB)k=(Ak)B=A(Bk) k - число

2. (A+B)C=AB+AC

3. (AB)C=A(BC)

14. Единичная матрица. Обратная матрица.

Единичная матрица:

E=(1,0,0)

0,1,0

0,0,1

Свойства единичной матрицы:

1) k=(k1,k2,…,kn) Ek=E1k1+E2k1+…+Enkn=k

2) для любой квадратной матрицы А выполняется следующее равенство: AE=EA=A

Обратная матрица:

Пусть A — квадратная матрица порядка n. Квадратную матрицу B того же порядка называют обратной к A, если AB = BA = E, где E — единичная матрица порядка n.

Обратную матрицу обозначают A(−1)

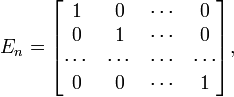
Теорема об обратимости невырожденной матрицы:

Каждая невырожденная матрица A обратима.

Доказательство: из условия теоремы=> что система n-мерных векторов A линейно не зависима, т.к. в системе А1,А2,…,Аn Ei векторов больше чем их размерность(размерность n, а векторов n+1)=> Ei разлагается по системе линейно не зависимых векторов А, при любом i.

E1=k1A1+k2A2+…+knAn

E2=l1A1+l2A2+…+lnAn

………………………….

En=t1A1+t2A2+…+tnAn

В качестве элементов 1-го столбца матрицы В, возьмём коэффициенты разложения E1, в качестве второго E2 и т.д.

B=(k1,l1,…,t1)

k2,l2,…,t2

…………

kn,ln,…,tn , тогда E1,E2,…,En можно рассписать:

E1=(AB)1;E2=(AB)2;…;En=(AB)n

В силу леммы о невырожденности матрицы AB=E=>BA=E=> матрица В обратная для А.

Теорема : Если матрица А обратима,то её столбцы A1,A2,…,An образуют линейно не зависимую систему векторов.

Доказательство: рассмотрим произвольное разложение нулевого вектора по системе столбцов А : k1A1+k2A2+…+knAn= θ

AE1=A1;…;AEn=An

k1(AE1)+k2(AE2)+…+kn(AEn)= θ

A(k1E1+k2E2+…+knEn)= θ

Умножаем слева на матрицу В(обратная для А)

BA(k1E1+k2E2+…+knEn )= θ

Т.к. E1,…,En линейно не зависимая система, то это равенство выполняется только если ki=0=>сисмема векторов А линейно не зависима=>система векторов образующая матрицу А линейно не зависимая.

Следствие из теорем: Матрица обратима тогда и только тогда, когда она невырождена.