40. Производные и дифференциалы высших порядков.

если функция имеет в каждой точке конечную производную , то производная функции в точке называется производной -го порядка функции в точке и обозначается одним из символов .

Таким образом,

Наконец, мы будем говорить, что функция раз дифференцируема в точке , если в некоторой окрестности этой точки она имеет конечную производную порядка (а стало быть имеет и все производные , ,…, ) и функция дифференцируема в точке .

41. Формула Тейлора для многочлена.

Формула называется формулой Тейлора в точке для многочлена степени .

42. Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).

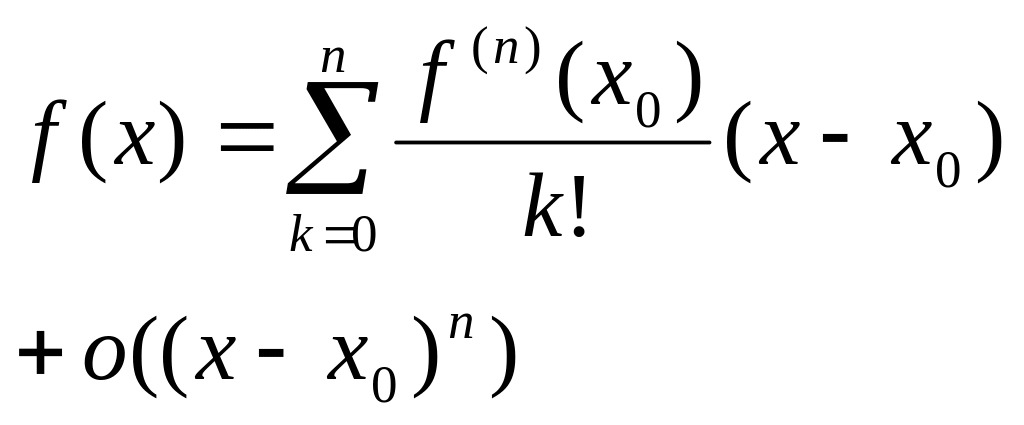называют, соответственно, формулой Тейлора с остаточным членом в форме Пеано или, также, локальной формулой Тейлора.

43.Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.

(формула Тейлора с остаточным членов в форме Лагранжа), (формула Тейлора с остаточным членом в форме Коши).

44.Разложение элементарных функций по формуле Тейлора.

n^о4. Разложение некоторых элементарных функцией по формуле Тейлора.Если , то формула Тейлора функции имеет особенно простой вид: (1)В этом случае она называется формулой Маклорена. Остаточный член в ней в форме Пеано, Лагранжа и Коши, соответственно, имеет вид , ,и .по формуле Маклорена. . Пусть . Эта функция имеет производные любого порядка и в любой точке (в таких случаях говорят, что функция бесконечно дифференцируема на всей числовой оси).

Как известно

Поэтому формула Маклорена функции имеет вид ( ):

где остаточный член можно записать в любой из форм: ( в форме Пеано) ( в форме Лагранжа)и (в форме Коши),где точка в каждой из двух последних формул лежит между точками и .

45. Правило Лопиталя.

Теорема 1. Пусть функции и дифференцируемы на конечном или бесконечном интервале , на и (1) Тогда если существует конечный или бесконечный предел (2)то существует и равный ему предел , т.е. (3)

Замечание 1. Аналогичное утверждение справедливо, если в условиях этой теоремы заменить всюду на .

Д о к а з а т е л ь с т в о теоремы 1. Возможны два случая: 1) - конечно и 2) . Рассмотрим сначала случай, когда, например, – конечное. Доопределим функции и в точке , положив

Тогда, с учетом условия (1), каково бы ни было , в силу дифференцируемости этих функций на интервале они будут непрерывными на отрезке . Следовательно, на всяком таком отрезке функции и удовлетворяют условиям теоремы Коши о среднем значении. Поэтому на любом таком отрезке существует такая точка , что

(4)

Заметим, что здесь по условию теоремы . Кроме того,

(поскольку , то это равносильно тому, что ). Действительно, в противном случае, по теореме Ролля, нашлась бы такая точка , что . Но это противоречит условию теоремы, в частности тому, что на . Из сделанных выше замечаний следует, что равенство (4) можно переписать в виде .

Но, так как , то это равносильно равенству .Учитывая теперь (2) и то, что при , в силу последнего равенства и теоремы о пределе суперпозиции, имеем .Рассмотрим второй случай, когда, . Тогда не уменьшая общности можно считать, что

Теорема 2. Пусть функции и дифференцируемы на конечном или бесконечном интервале , на и

.Тогда если существует конечный или бесконечный предел

то существует и равный ему предел

.Замечание 2. Аналогичное утверждение справедливо и при замене условия на условие .