35. Дифференцирование сложной функции

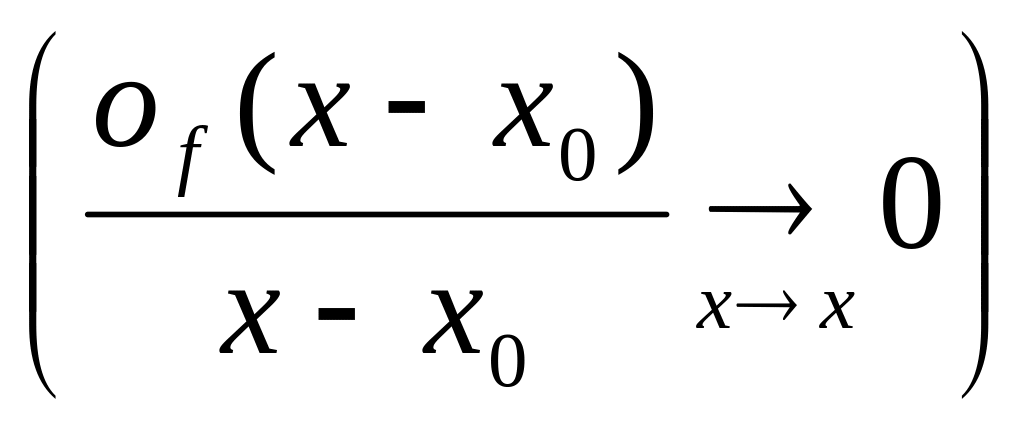Пусть функция определена на интервале , а функция определена на интервале , причем . Тогда если функция дифференцируема в точке , а функция дифференцируема в точке , то сложная функция дифференцируема в точке и Д о к а з а т е л ь с т в о. В силу дифференцируемости функций и , соответственно, в точках и , имеем _{и как известно} , Из (3) и (4) следует, что

Подставляя сюда , и используя затем равенство (2), получим

и, следовательно,

Поскольку функция непрерывна в точке , а функция непрерывна в точке и , то по теореме о непрерывности сложной функции .

А так как, кроме того,

то из (5) следует, что существует конечная производная

и имеет место равенство (1). Для завершения доказательства теоремы остается вспомнить, что существование конечной производной равносильно дифференцируемости функции в точке .

36. Дифференцирование обратной функции.

Пусть функция строго монотонна и непрерывна в окрестности точки . Пусть, кроме того, функция дифференцируема в точке и . Тогда обратная к ней функция дифференцируема в точке , причем

Д о к а з а т е л ь с т в о. Из условий теоремы следует, что существует конечный, отличный от нуля предел

Тогда по теореме о пределе частного существует конечный предел Рассмотрим функцию

В силу строгой монотонности функции она определена в проколотой окрестности точки . В точке функция имеет конечный предел (2). Поэтому если доопределить ее в этой точке равенством

,то она будет непрерывной в этой точке. Тогда учитывая, что функция непрерывна в точке (как обратная к непрерывной, строго монотонной функции ), по теореме о непрерывности суперпозиции заключаем, что сложная функция будет непрерывной в той же точке и, следовательно, Поскольку в некоторой проколотой окрестности точки в силу равенства (3) имеет место равенство

,и предел функции в данной точке не зависит от того, как она определена в этой точке, то из (4) следует, что функция дифференцируема в точке и имеют место равенства (1)

37.Дифференцирование элементарных функций. Таблица производных.

n^о 1. Таблица производныхЭлементарные функции (за исключением функций и ) дифференцируемы в своих областях определения, причем справедливы следующие формулы (они обосновываются в следующих пунктах):

. . .

. . .

. , . , .

. , .

. , . n^о 2. Показательная и логарифмическая функции. Здесь будут установлены формулы , , и из предыдущего пункта. Прежде всего, напомним, что

и . Теперь используя равенство (2) и то, что постоянную можно выносить за знак предела получим: =

Таким образом установлена формула .

Далее, так как функция является обратной к функции , по формуле для производной обратной функции имеем:

= .Следовательно, установлена и формула .Для вывода формулы установим формулу дифференцирования показательно-степенной функции. где и – дифференцируемые на некотором промежутке функции, причем на .Используя формулу для производной сложной функции, формулы и , а также формулу для производной произведения функций будем иметь

Таким образом, .В частности, если здесь , а , то

,т.е. установлена и формула . Формула вытекает из формулы 2⁰ в силу формулы дифференцирования обратной функции:

(здесь , ).n^о 3. Производная степенной функции.Предварительно представив степенную функцию ( )в виде ее производную вычислим с помощью формулы дифференцирования сложной функции: Формула , таким образом, также доказана.n^о 4. Тригонометрические функции.Используя формулу

,а также известный замечательный предел ,по определению производной с учетом непрерывности функции будем иметь

Далее, по правилу дифференцирования сложной функции получим

Производные от функции и вычисляются с использованием установленных выше формул и и формул дифференцирования частного. Читателю предлагается сделать это самостоятельно.

n^о 5. Обратные тригонометрические функции.Формулы выводятся с помощью формулы для производной обратной функции и одной из соответствующих .Например, функция

Является обратной к функции , ( ). Поэтому

Перед радикалом здесь берется знак «+», поскольку при .Аналогично вычисляется производная от функции . Далее, функция является обратной к функции . Поэтому

Аналогично вычисляется производная от функции