Глава 2

ПРОГНОЗИРОВАНИЕ КАЧЕСТВА И СОСТОЯНИЙ КОНСТРУКЦИИ

2.1. Аналитический и вероятностный методы прогнозирования

Операцией прогнозирования на­зовем мероприятие, направленное на предсказание исправной работы объекта пли его состояний на некоторый наперед задан­ный момент времени и состоящее из постановки задачи, форми­рования математической модели, ее решения и оценки резуль­татов.

Прогнозирование базируется на экспериментальных данных или статистическом материале о значениях показателей качест­ва объекта в функции времени. Эти показатели являются исход­ными для построения эмпирических функций изменения пара­метров, которые затем используются для формирования мате­матических моделей.

Результаты прогнозирования считаются удовлетворительны­ми, если значения показателей качества на прогнозируемый период времени больше допустимых значений или ожидаемая вероятность безотказной работы Р_ф больше заданной Р_д:

Р_ф≥Р_д; К_iф≥К_iд

где К_iф, К_iд — значение фактическое i-ro показателя качества и допустимое.

Рассмотрим вначале аналитическое прогнозирование с ис­пользованием экстраполяции эмпирических функций. В общем случае предсказание качества базируется на результатах иссле­дований технического состояния объекта или на статистических данных эксплуатации совокупностей сопоставимых объектов.

Учитывая изложенное, можно выделить два способа прогно­зирования: 1) инструментальное (аналитическое), основанное на результатах исследования экспериментальным путем харак­теристик объекта; 2) статистическое (вероятностное), основанное на опыте и результатах эксплуатации сопоставимо подобных объектов.

Предположим, что исследуемый объект можно довольно полно охарактеризовать некоторым информативным показате­лем качества x(t). Известны его значения в некоторые моменты времени t₁ и t₂. Кроме того, известно его допустимое значение х_д. Требуется определить значение показателя качества в мо­мент времени t_п по условиям прогнозирования.

В математическом смысле поставленная задача является задачей экстраполяции. Для ее решения воспользуемся экспе­риментальными данными.

Известны x(t₁), x(t₂). Требуется определить x(t_п). В простей­шем случае можно предположить, что показатель качества изме­няется линейно, тогда функция изменения показателя качества опишется зависимостью x(t)=а+b(t).

Если найдены неизвестные а и b, то, подставив вместо t время, требуемое по прогнозу t_п определим значение x(t_п); если x(t_п)>>х_д, то объект будет работоспособным на прогнозируемом интер­вале времени.

На основе экспериментальных данных составим систему урав­нений, которая позволяет рассчитать неизвестные а и b

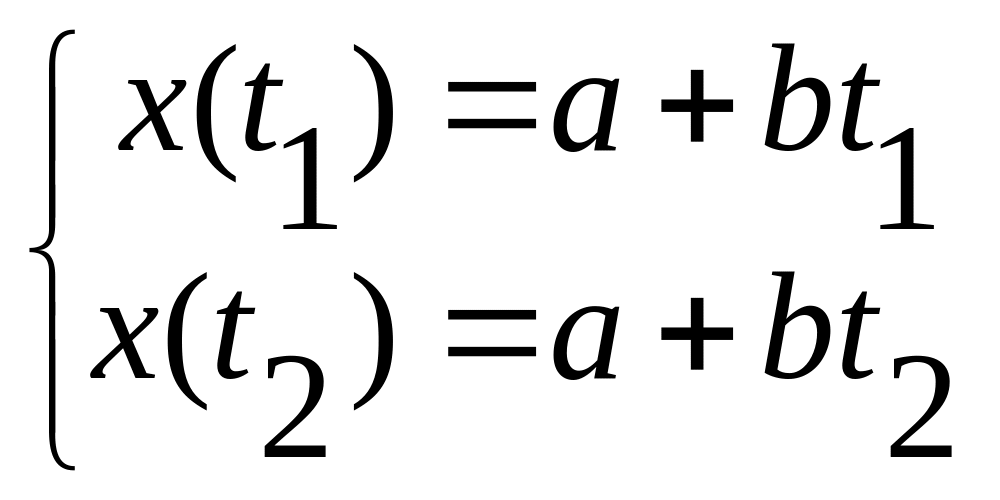
Решив систему уравнений, получим

В данном случае произведено прогнозирование по двум точкам значения показателя качества, измеренным в моменты времени t₁ и t₂. Такой прогноз состоятелен, если заранее изве­стна тенденция к монотонному изменению показателя качества.

Рассмотрим более сложный пример с оценкой точности эмпи­рических формул, используемых для построения прогноза. Пред­положим, что мы имеем экспериментально полученные значения прогнозируемого параметра x(t) для моментов времени

t₁,t₂,…,t_n

Требуется определить значение x(t) для момента времени t_k+1.

Значения параметра x(t) для дискретных моментов времени сведем в табл. 2.1.

Таблица 2.1

Значения x(t)	x(t1)	x(t2)	…	x(tk)	x(tk+1)
Дискретные моменты времени t	t1	t2	…	tn	tk+1

Предположим, что закон изменения параметра описывается полиномом, например второй степени, т. е.

В нашем случае имеется избыточность значений x(t_i), так как k > 3, а для определения коэффициентов нужно всего три значения x(t_i). Чтобы решить, какие значения x(t) следует взять из таблицы, рекомендуется поступить следующим образом. Сначала из таблицы берут три первых значения, затем — три вторых и т.д. Составляют системы уравнений для каждой тройки значений x(t_i), например для первой

Решив систему уравнений, рассчитывают а⁽¹⁾, b⁽¹⁾, с⁽¹⁾. Затем, поступая аналогично предыдущему, определяют значения неиз­вестных для второй группы уравнений, т. е. а⁽²⁾, b⁽²⁾, с⁽²⁾ и т. д.

Таким образом, будем иметь столько коэффициентов, сколько групп. Допустим, их было s, тогда x(t) можно подсчитать по лю­бой тройке коэффициентов

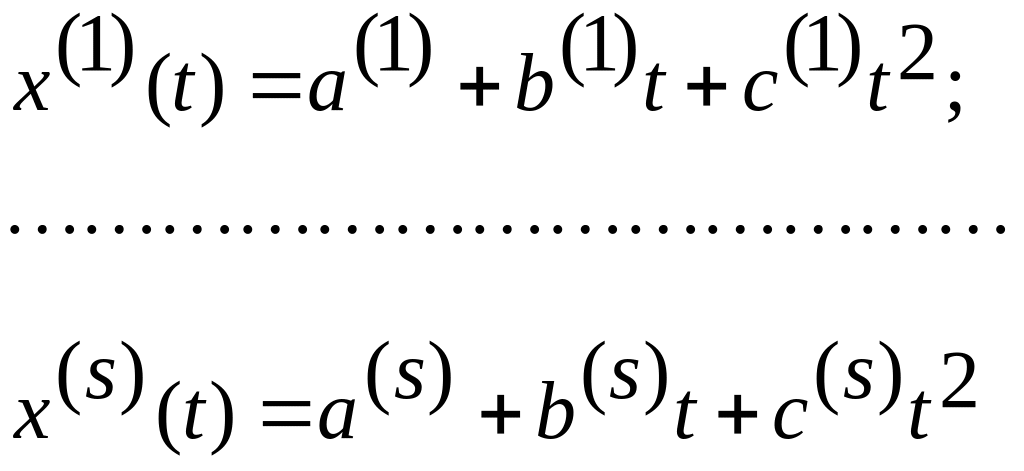
Теперь выясним, какая группа из 5 наиболее подходяща. Оценку произведем по погрешностям, которые получаются при расчете по каждой из формул. Результаты сведем в табл. 2.2.

Таблица 2.2

табличное	Формула (1)			Формула
	(ti)	ξ		(ti)	ξ
x(t1)	x(1)(t1)	ξ11		x(s)(t1)	ξ(1)1
x(tk)	x(1)(tk)	ξ1k		x(s)(tk)	ξ(s)k
		∑ξi			∑ξ(s)i

Подсчитываем суммарные значения погрешности, получен­ные по каждой из формул:

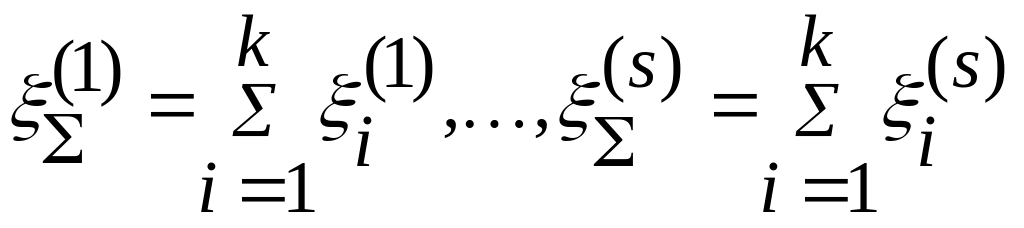
Находим минимальное значение . Воспользуемся той из формул, которая дает минимальное значение суммарной погреш­ности. Пусть в нашем случае это формула j. тогда

Значение прогнозируемого параметра для времени t_k+1 составит

Описанный метод прогнозирования является не единственным, однако он прост и позволяет получить удовлетворительные результаты. Этот метод называют методом средних.

Чтобы повысить точность, целесообразно увеличивать сте­пень полинома.

Таким образом, с помощью метода средних по эмпирическим табличным значениям прогнозируемого параметра можно найти эмпирическую зависимость в виде полинома k-й степени (k = 1, ..., n) а затем определить значение прогнозируемого пока­зателя качества.

Здесь мы решаем две задачи: определяем вид эмпирической зависимости и находим значение прогнозируемого параметра.

Рассмотрим графический метод описания экспериментально полученных зависимостей показателя качества подходящими эмпирическими формулами. Этот метод удобен для описания эмпирических зависимостей показательными функциями (рис. 2.1).

Предположим, что получены экспериментальные значения па­раметра x(t) в некоторые дискретные моменты времени t₁ . . ., t_k.

Сведем полученные значения х (t_i) в табл. 2.3.

Таблица 2.3

Значения показателя качества х(ti)	х(t1)	х(t2)	…	х(tk)	х(tk+1)
Моменты времени ti	t1	t2	…	tk	tk+1

Построим график дискретных значений x(t_i) и оценим его качественно. Если исследуемая функция х(t_i) не имеет особен­ностей, то, перейдя к непрерывному значению х(t), находим, что подходящей зависимостью для ее описания является x(t)=at^b.

Логарифмируем показательную функцию

Перейдем к новым переменным, обозначив

,

тогда получим уравнение прямой. Построим ее в логарифмическом масштабе и проверим линейность Y = lga + bХ.

Чтобы определить неизвестные а и b, воспользуемся крайними значениями x(t₁) и x(t_k) из табл. 2.3. Составим систему урав­нений

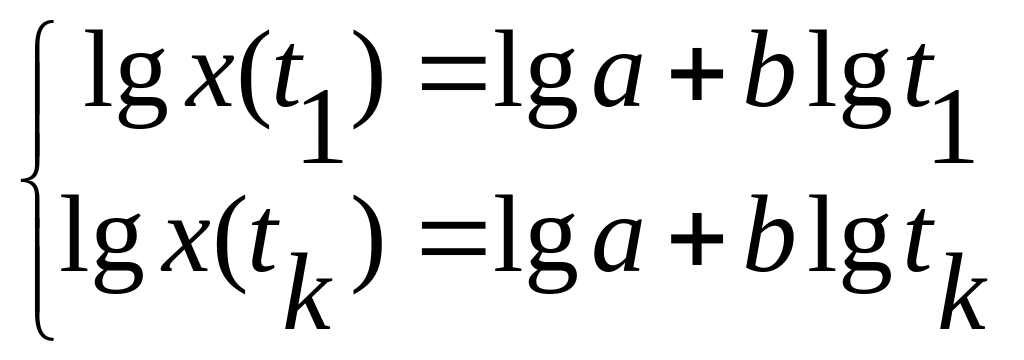
Имеем два уравнения и две неизвестные, следовательно, за­дача легко решается. Находим значение показателя качества в момент времени t_k+1 x(t_k+1)=at^b_k+1

Если x(t_k+1) ≥ х_д, то исследуемое изделие к моменту t_k+1 будет исправным.

Удовлетворительные результаты при использовании графи­ческого метода получают при условии, что прогноз строится не более двух шагов вперед, т. е. для t_k+2.

Рассмотрим операцию прогнозирования вероятности безот­казной работы аппаратуры на основании статистических дан­ных.

Рис. 2.1. График экспериментально полученных значений функции X(t)

Рис. 2.2. График изменения коэффициента усиления в функции времени

Возьмем для примера аналоговое устройство. Типичным пред­ставителем этих устройств является операционный усилитель.

В простейшем случае его основной информативный параметр коэффициент усиления K, характеризующий отношение выходной величины к входной, постоянен: K = U_выx/U_вх, где U_выx — выход­ной сигнал; U_вх — входной сигнал.

При наличии помех внутреннего и внешнего характера, на­пример старения элементов, колебаний питающих напряжений, он может со временем изменяться. Следовательно, коэффициент усиления в общем случае является случайной функцией с мате­матическим ожиданием m_k. Факторы, вызывающие отклонение ΔK, многочисленны и имеют различную физическую природу, поэтому естественно предположить нормальность распределения отклонений ΔK (рис. 2.2).

Для любого технического устройства существуют допустимые изменения коэффициента усиления ±ΔK. Вероятность того, что коэффициент усиления не выйдет за допустимые значения, со­ставляет

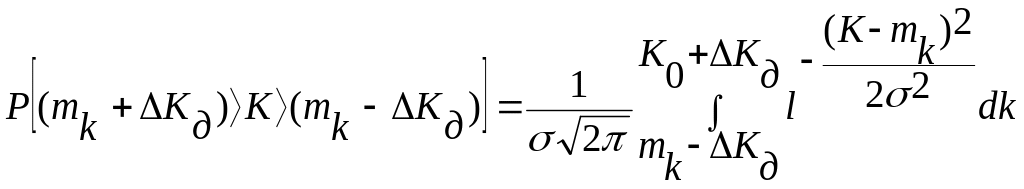
При нормальном распределении, учитывая симметричность плотности распределения и используя функции Лапласа, можно записать

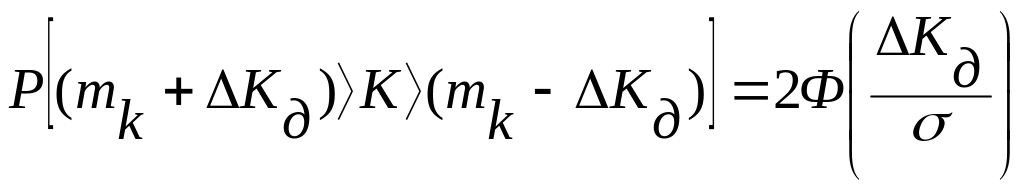
Фактическая картина изменения коэффициента усиления во времени сложна, так как всегда присутствуют случайные деста­билизирующие факторы, связанные с износом, старением, изме­нением температуры, влажности и т. д.

В простейшем случае математическое ожидание коэффициента усиления описывается линейной функцией вида

где С — постоянный коэффициент ста­рения.

Функция m_k(t) изображена на рис. 2.2, где f(m_k,t₀), f(K₁,t₁)— плотности распределения в сечениях t₀ и t₁ соответственно.

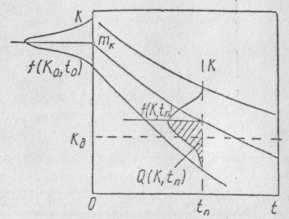
Рис. 2.3. График, поясняющий определение вероятности безот­казной работы к моменту вре­мени t_n

В общем случае функция измене­ния математического ожидания может описываться полиномами более выс­ших порядков, например второго или третьего: m_k(t) = m_к(0) — c₁t — c₂t², m_k(t) = m_k(0) — c₁t — c₂t² — c₃t³, где с₁, с₂, c₃ — некоторые коэффициенты, характеризующие скорость изменения или ускорения изменения К во временя.

По результатам эксплуатации установлено, что разброс ко­эффициента усиления со временем увеличивается, т. е. увеличи­вается его дисперсия.

При произвольном законе изменения математического ожи­дания коэффициента усиления вероятность его выхода за допу­стимое значение в момент времени t_п (рис. 2.3):

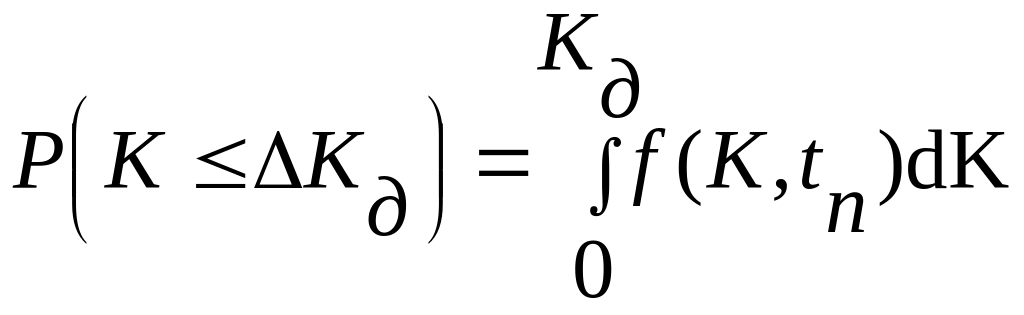
Если известна плотность распределения коэффициента усиле­ния в сечении t_п, то нетрудно вычислить вероятность того, что коэффициент усиления не выйдет за допустимый предел K_д. Заме­тим, что при нелинейной функции m_k(t) распределение плотности вероятности f(K,t) отлично от нормального в любом из сечений случайного процесса.

Задачу о нахождении вероятности недостижения в момент времени t_п процессом значения K_д можно решить, используя плотность распределения случайного времени (рис. 2.4):

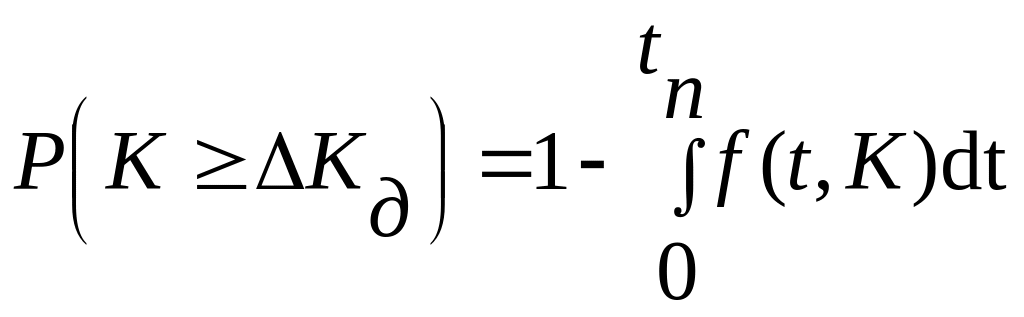
Если изделие характеризуется несколькими параметрами; то определяют вероятности недостижения этими параметрами допустимых значений и по минимальной полученной вероятно­сти судят о наиболее опасном и критическом параметре.

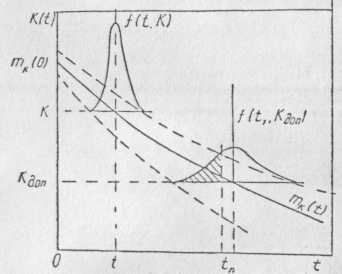
Рис. 2.4. График, поясняющий мето­дику определения вероятности безот­казной работы при изменении парамет­ра К при эксплуатации

Каждый параметр, как пра­вило, имеет присущий только ему закон плотности распреде­ления параметра и его измене­ний во времени. Допустим, что объект характеризуется тремя параметрами а (t), b(t), c(t), ко­торым определены допустимые значения а_д, b_д, с_д (рис. 2.5). Найдем для некоторого момента времени t_п вероятность безот­казной работы объекта через вероятность отказа. Учитывая совместимость и предполагая не­зависимость параметров, найдем

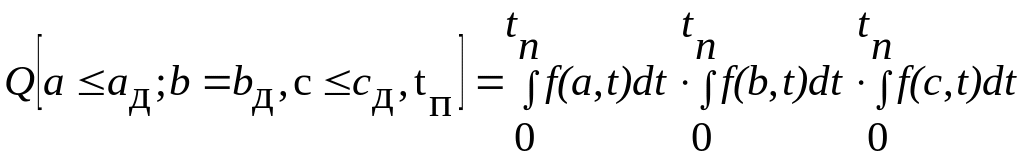
Следовательно, вероятность безотказной работы составит

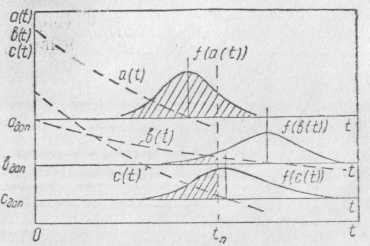
Рис. 2.5. График, поясняющий определение времени безотказной работы изделия по со­вокупности трех параметров

Подсчитывая вероятности безотказной работы по каждому из параметров, находят наиболее критичные параметры. Трудности при прогнозировании ка­чества б данном случае связаны в основном с опре­делением законов распре­деления параметров, кото­рые могут быть получены лишь по результатам эксплуатации.

Если P(t_п)≥ P_д(t_п), то результаты прогнозирования вероят­ности безотказной работы до времени t_п считаются положитель­ными.

2.2. Прогнозирование состояний объекта на основе теории дискретных цепей Маркова

Основу технических средств современных сложных систем составляет электронная аппаратура. Так, ЭВМ — техническое средство вычислительных систем, систем автоматизации проек­тирования, систем управления сложными динамическими объек­тами и т. д. Рассмотрим задачу прогнозирования состояний объекта на примере вычислительной системы, являющейся сложным объединением однородных или разнородных техниче­ских устройств, которые могут находиться в различных состоя­ниях, т. е. работать, быть в резерве, стоять на ремонте и т. д. Состояние вычислительного комплекса является случайным, зависящим от его загрузки или от состояния надежности. После­довательность состояний в функции времени можно рассмат­ривать как случайный процесс. Оценить вероятности состояний вычислительного комплекса наиболее удобно с помощью теории марковских процессов (цепей).

Суть операции прогнозирования на основе теории дискрет­ных цепей Маркова состоит в предсказании вероятности состо­яний объекта на некоторый наперед заданный шаг.

Постановка задачи заключается в формулировании условий операции, т. е. в описании объекта и определении цели. Исходя из поставленной задачи выбирают математическую модель. В данном случае применена модель марковских процессов с дискретными состояниями и дискретным временем [2].

Рассмотрим вопросы теории марковских процессов, которые будут использованы при решении операций прогнозирования состояний объекта.

Процесс является марковским, если для каждого момента времени t вероятность любого состояния в будущем (при t>t₀) зависит только от ее состояния в настоящем, т. е. при t=t₀ и не зависит от того, как протекал процесс в предыдущем, т. е. при t<t₀

Широкое распространение получила теория процессов с диск­ретными состояниями. Это объясняется тем, что фактическое состояние объекта оценивается именно в дискретном плане (ра­ботает, не работает, ремонтируется, дежурит и т. д.).

Случайный процесс называют процессом с дискретным состо­янием, если можно перечислить состояния системы S_i одно за другим [2, 3]. Переход из одного состояния в другое происхо­дит скачком.

Предположим, что вычислительная система состоит из двух вычислительных устройств. Возможны четыре состояния: S₁ — оба устройства работают; S₂ — одно отказало, а второе рабо­тает; S₃ — второе отказало, а первое работает; S₄ — оба устрой­ства отказали.

Эти состояния отображены графом состояния (рис. 2.6).

Различают процесс с дискретным и непрерывным временем. Если переходы системы из одного состояния в другое происходят в строго определенные, заранее известные моменты времени, то такой процесс называют процессом с дискретным временем.

Если переход системы из одного состояния в другое проис­ходит в заранее неизвестные моменты времени, то такой случайный процесс называют процессом с непрерывным временем.

Рассмотрим процесс с дискретным временем. Система мо­жет находиться в одном из состояний Si, S₂, ..., S_n. Переход в эти состояния осуществляется в дискретные моменты времени t₁, t₂, …, t_n. Эти моменты времени составляют шаги 1, 2, ..., n. Следовательно, последовательность состояний является функ­цией шагов, т. е. S₁(l), S₂(2), ..., S_n(n). Заметим, что система при некотором i-м шаге может не переходить в другое состояние, а оставаться в прежнем. Каждое состояние оценивается веро­ятностью, например, P_i(k). Это означает, что вероятность i-го состояния наступает при k-м шаге. Переход из состояния в сос­тояние происходит с некоторой вероятностью P_ij. Это означает, что из состояния i в состояние j система переходит с вероятно­стью P_ij.

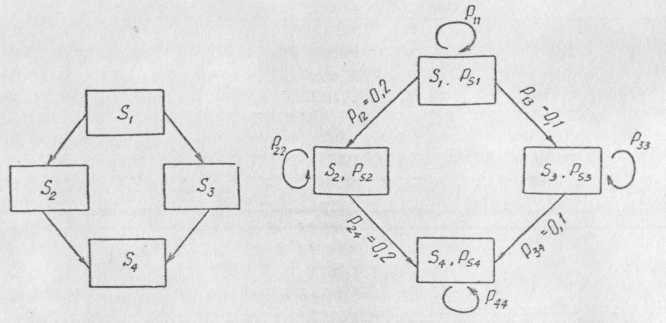
Рис. 2.6. Граф состояний системы

Рис. 2.7. Размеченный граф состояний

Всевозможные состояния при k-м шаге составляют полную группу, поэтому результирующая вероятность состояний равна единице при любом шаге.

Если известны вероятности переходов из одного состояния в другое и они не зависят от номера шага, то состояния систе­мы составляют однородную марковскую цепь. Если система задержалась в некотором состоянии i, то вероятность непере­хода записывается в виде Р_ii. Если вероятности переходов отшага к шагу изменяются, то такая цепь состояний называется неоднородной марковской цепью с дискретным временем.

Вероятность переходов для системы можно записать ввиде матрицы

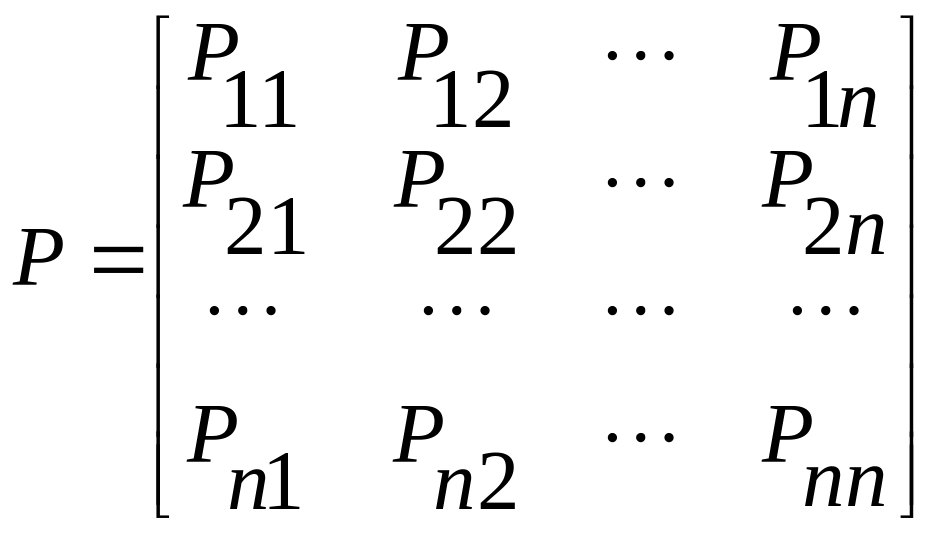
Если некоторые вероятности переходов равны нулю, то пе­реход системы из состояния в состояние невозможен. По глав­ной Диагонали матрицы вероятностей переходов стоят вероят­ности непереходов, т. е. вероятности того, что система не перей­дет в другое состояние, а задержится в прежнем состоянии.

Граф состояний, на котором приведены вероятности переходов, называют размеченным. Такой граф изображен на рис. 2.7. Для него справедливо

Эти уравнения используются для определения вероятностей неперехода системы из одного состояния в другое.

Имея размеченный граф состояний системы, найдем веро­ятности состояний для различных шагов.

Исходное состояние системы характеризуется вероятностями

При первом шаге вероятности состояний составляют

т. е. вероятности состояний равны вероятностям переходов.

При втором шаге

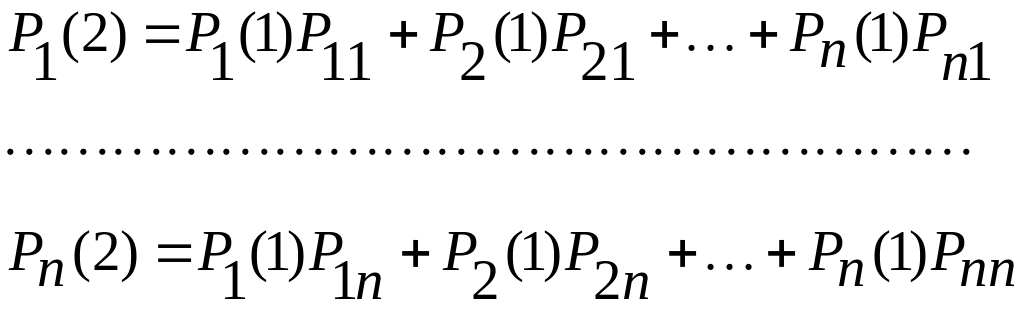
или

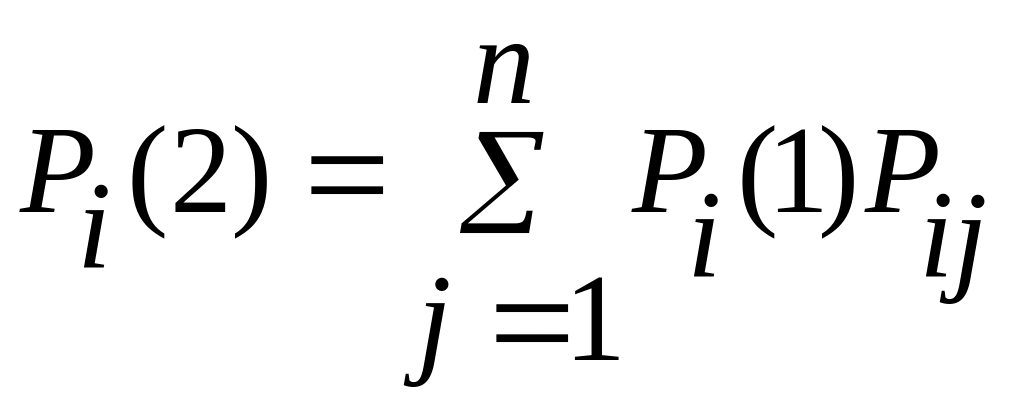
где i = 1, 2, .,., n.

Аналогично можно определить вероятность состояний для любого k-то шага

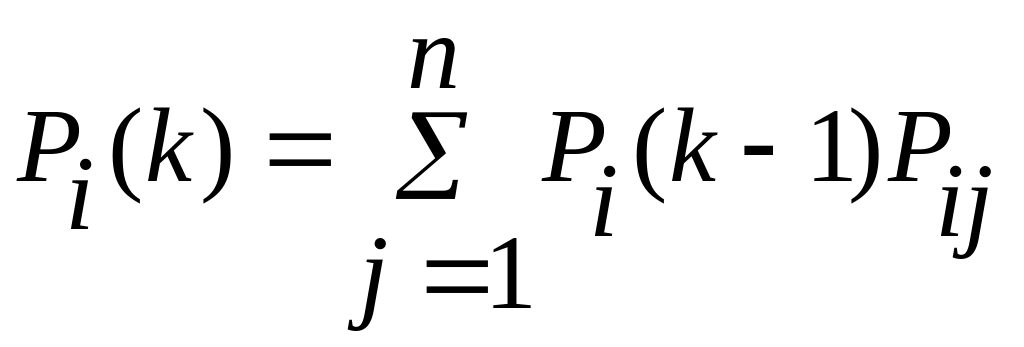
Эта формула может быть использована для определения номера шага, при котором достигается допустимое значение вероятности прогнозируемого состояния.

Алгоритм поиска номера шага для максимизируемых состоя­ний записывается в виде

_где ξ — некоторая величина, выбираемая из области допустимых отклонении значений вероятности прогнозируемых состояний.

Аналогично для минимизируемых состояний с той разницей, что допустимые значения вероятностей должны быть больше фактических.

Пример. Задан размеченный граф состояний (рис. 2.7), допустимое значение вероятности для третьего состояния Рз(k) = 0,2, ξ = 0,03. Требуется определить номер шага, при котором значение вероятности третьего состояния окажется в допусти­мых пределах.

Решение. Определим вероятности непереходов

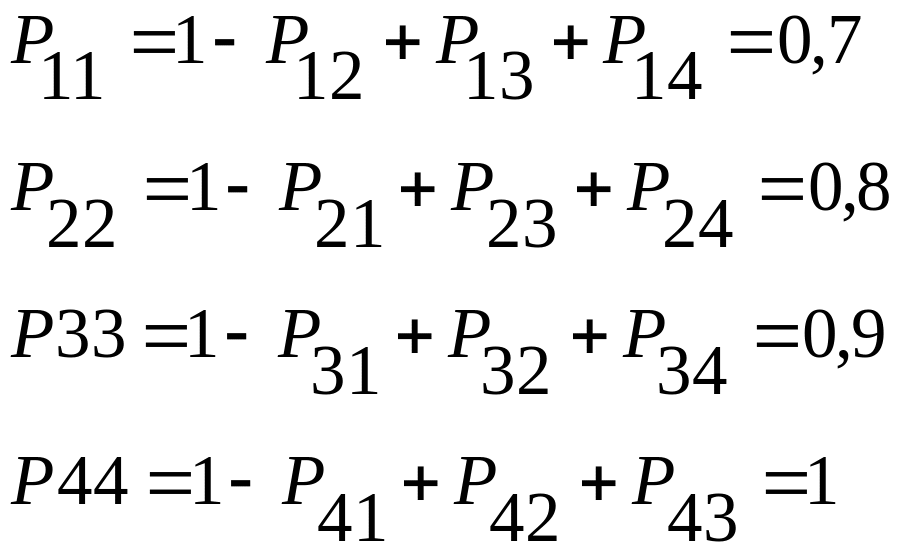
Составим матрицу вероятностей переходов

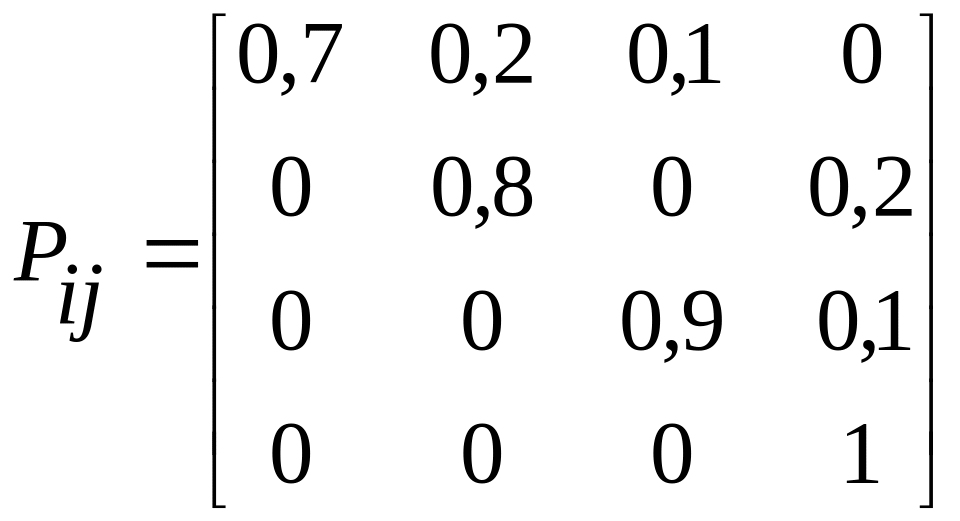
Определим вероятности состояний для нулевого и первого шагов

при нулевом шаге

при первом шаге

Вычислим вероятности состояний для второго шага

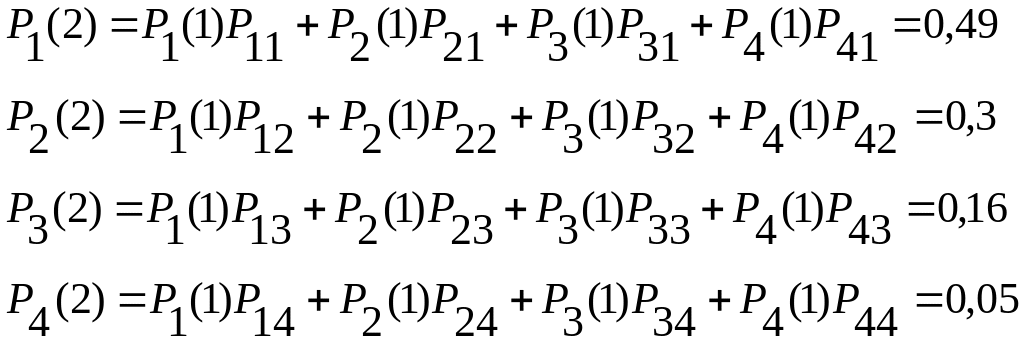
Проверяем:

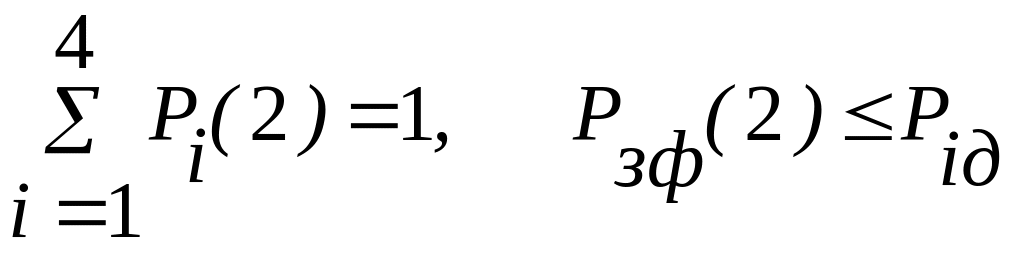
Условие выполняется. Шаговый процесс продолжаем. При третьем шаге

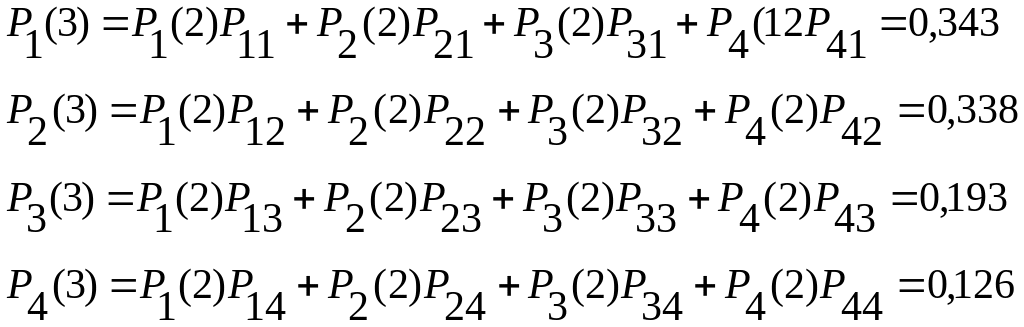
Проверяем:

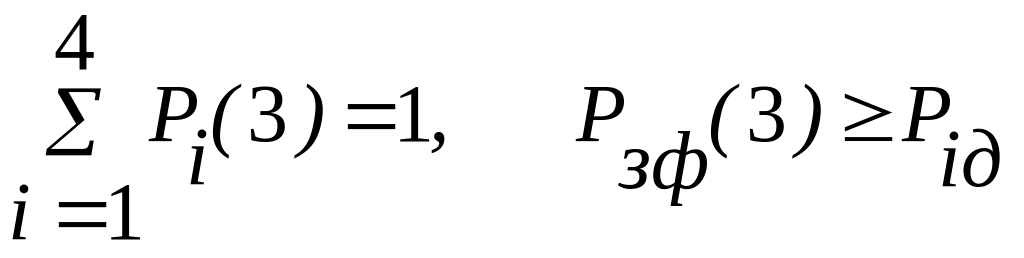
При проверке условия оказывается, что (Р_iд(3) — Р_iф(3)) < ξ, но больше нуля, следовательно, операция прогнозирования со­стояний объекта выполнена, число шагов равно трем.

На основании полученных ре­зультатов для наглядности реше­ния построим график вероятностей состояний вычислительного комп­лекса (рис. 2.8).

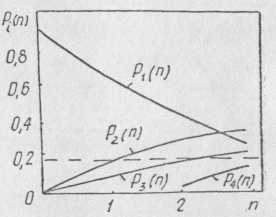
Рис. 2.8. График состояний вы­числительного комплекса

В более общем случае вероятности состояний системы описываются не­однородной марковской цепью. В этом случае вероятности переходов Р_ij являются функциями шагов, т. е. зависят от номера шага. Тогда веро­ятность S_i-гo состояния находится по формуле

Таким образом, для вычисления вероятностей состояний необходимо иметь заданную последовательность матрицу переходов

а также знать исходное состояние системы.