3.3. Линейное программирование в решении конструкторских задач

Методы линейного программирования широко распростране­ны в конструкторской практике. Они позволяют найти опти­мальное решение, если целевая функция описывается линейно комбинацией своих составляющих, кроме того, линейны ограни чения, а элементы решения — неотрицательны

Постановку задачи линейного программирования широко распространены в конструкторской практике. Они позволяют найти опти­мальное решение, если целевая функция описывается линейной комбинацией своих составляющих, кроме того, линейны ограни­чения, а элементы решения — неотрицательны. Постановку задачи линейного программирования рассмотрим а конкретном примере. Предположим, что конструктор распо­лагает тремя видами комплектов проводов П₁ П₂, П₃, имею­щих соответственные стоимости С₁, С₂, С₃. Каждый комплект содержит алюминиевые и медные провода, причем в комплекте П₁ содержится: a₁₁ — алюминиевых, а₂₁—медных, в комплек­те П₂ содержится: a₁₂— алюминиевых и a₂₂ — медных прово­дов, в комплекте П₃ содержится: а₁₃—алюминиевых и а₂з — медных проводов.

Известно, что на монтаж установки расходуется алюминиевых проводов не менее b₁, а медных проводов — не менее b₂.

Задача состоит в определении необходимого количества каж­дого из комплектов с тем, чтобы смонтировать установку и за­тратить минимальное количество средств па приобретение комп­лектов.

Обозначим потребление количества комплектов через х₁, x₂, x₃. Пои этом не налагаем условий целочисленности на элемен­ты решения. С учетом известных стоимостей комплектов целе­вая функция, подлежащая оптимизации, имеет вид

Составим ограничительные уравнения

(3.4)

Первое уравнение описывает потребность в алюминиевых проводах, а второе — в медных.

Требуется найти неотрицательные значения элементов реше­ния минимизирующих целевую функцию с учетом ограничений.

Прежде чем перейти к непосредственному решению задачи, остановимся на некоторых общих вопросах, которые связаны с решением задач линейного программирования.

Прежде всего следует выяснить, всегда ли существует реше­те для всех неотрицательных x_i. Если такое решение сущест­вует то при каких условиях оно возможно? Убедившись в су­ществовании решения, можно перейти к отысканию экстремума целевой функции.

Для доказательства существования решения составим мат­рицу коэффициентов системы ограничительных уравнении

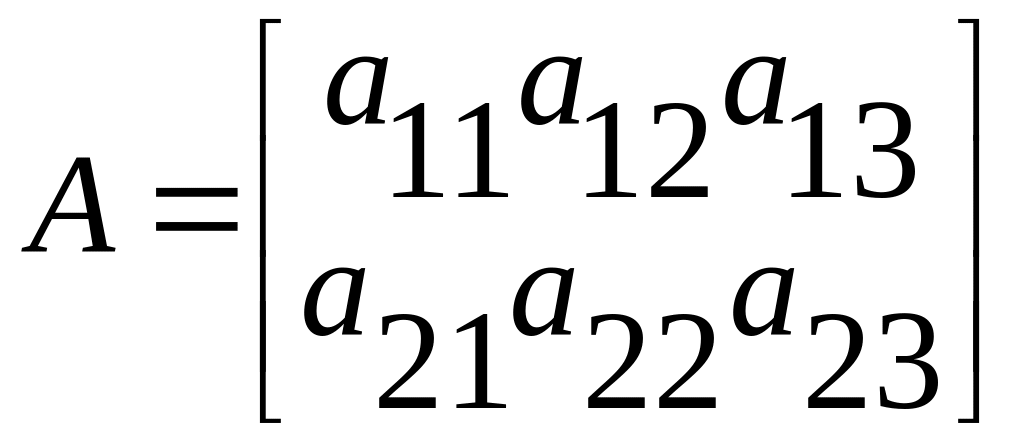
Затем составим расширенную матрицу

.

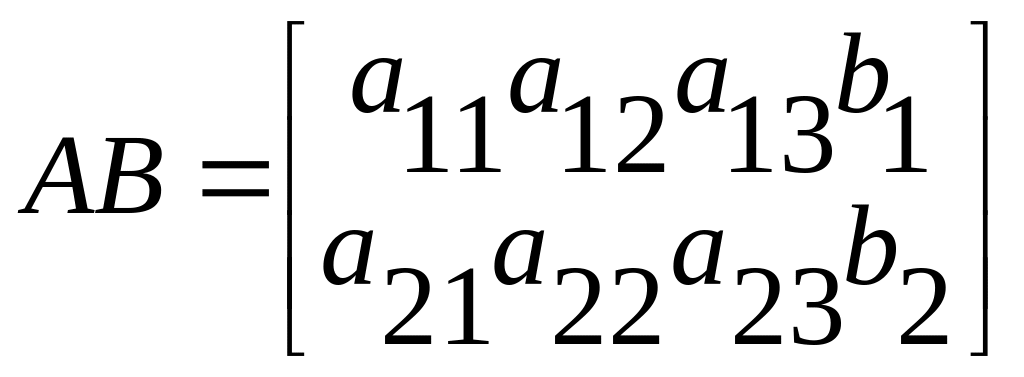Решение (3.4.) существует в том случае, если ранг матрицы системы равен рангу расширенной матрицы. Этим определяем совместимость уравнений, входящих в систему [3].

Напомним, что рангом матрицы называют наибольший поря­док отличного от нуля определителя, который определяют путем вычеркивания соответствующих столбцов и строк матрицы. В нашем случае

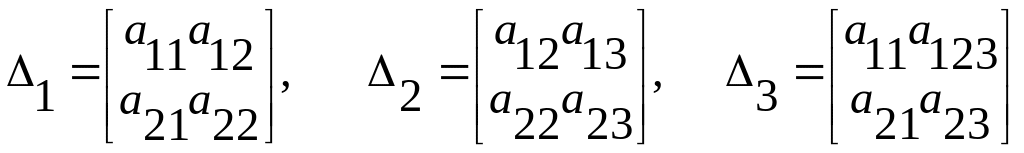
Если определители отличны от нуля, то, найдя (любой) оп­ределитель расширенной матрицы, отличный от пуля, убежда­емся, что условие равенства рангов соблюдается. Следователь­но, система совместима и имеет решение.

Предположим, что решение существует, тогда, обращаясь к системе уравнений (3.4.), замечаем, что она имеет бесконечное число решений, так как количество неизвестных на единицу больше числа уравнений. Будем решать задачу для случая, ког­да ограничительные уравнения представлены равенствами. При­дадим одной из переменных, например х_i значение свободной переменной, а остальные переменные х₂ и x₃ будем называть базисными. Свободной переменной можно придавать различные произвольные значения.

Выразим базисные переменные через свободную перемен­ную, для чего умножим первое ограничительное уравнение на a₂₂/a₁₂ и вычтем второе ограничительное уравнение, В результа­те получим

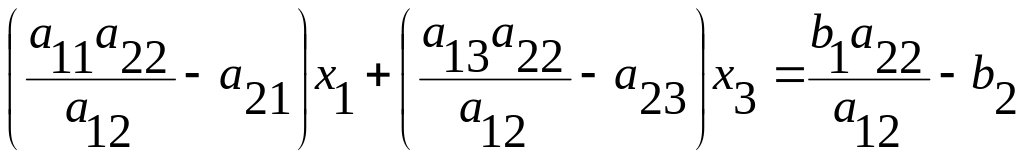
Обозначим коэффициенты при переменных через γ₁ и γ₃, а сво­бодный член через — D, тогда

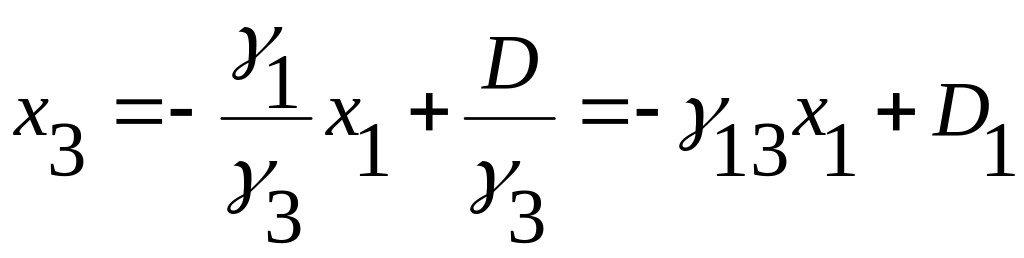
Подставим значение х₃ во второе уравнение, найдем х₂= -γ₁₂x₁ + D₂, где γ₁₂ — обозначение постоянного коэффициента, полученного в результате преобразования; D₂ — обозначение сво­бодного члена.

Подставим значения х₂ и x₃ в минимизируемую целевую функ­цию К = C₁x₁ +D₂ — γ₁₂x₁ — γ₁₃x₁ + D₁

Приведем подобные члены К = (С₁ —γ₁₂ — γ₁₃)x₁ + (D₂—D₁). Введем новые обозначения для коэффициента при x₁ и свободного члена, тогда К =γ₁*x₁ + D*.

Придавая различные значения свободной переменной х₁ бу­дем получать различные значения K. Очевидно, среди значения x₁ есть то, которое обращает в минимум целевую функцию. Для •отыскания этого значения свободной переменной (свободных переменных) существует ряд методов, на некоторых из них сле­дует остановиться. Покажем, что всегда можно перейти от ог­раничений, заданных неравенствами, к равенствам.

Система ограничительных неравенств имеет вид

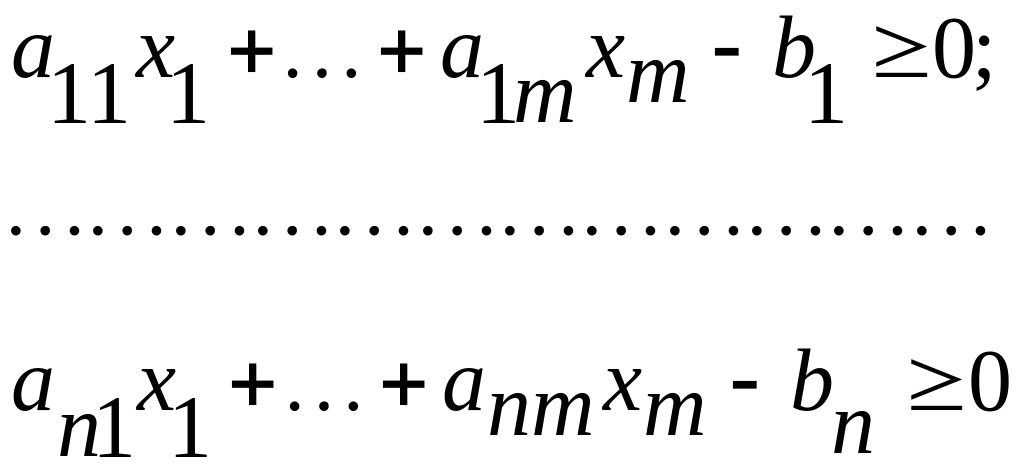
Введем новые переменные, больше нуля или равные нулю_г. тогда можно записать

.

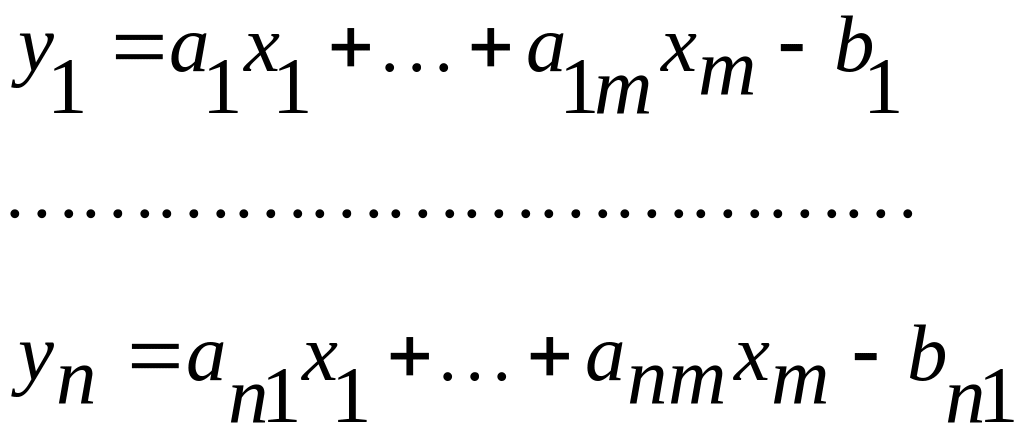В данном случае к имеющимся переменным прибавились-«добавочные» переменные y_i. В общей задаче переменных стало m+n. Для решения задачи поступают аналогично предыдущему случаю, т. е. собирают свободные и базисные переменные, но уже не из числа m, а из m+n.