3.6. Нелинейное программирование в задачах конструирования

Конструкторские задачи, имеющие нелинейные целевые функции пли нелинейные ограничения, приводят к необходи­мости решения задач оптимизации методами нелинейного про­граммирования.

Задача нелинейного программирования состоит в отыска­нии оптимального значения целевой функции

при ограничениях

где К —целевая функция (линейная или нелинейная); j = 1, . . ., n, f_i(x₁, ..., x_m) — ограничительные уравнения (линейные или нели­нейные); А—заданные условия задачи; X — элементы решения.

Задача является нелинейной, если целевая функция или любое из ограничений —нелинейны. В настоящее время не разработаны универсальные методы решения задач нелиней­ного программирования, поэтому, исходя из условий решаемой физической задачи, используют те или иные методы, например градиентные, случайного поиска, секущих плоскостей. Рассмот­рим некоторые из них.

1. Градиентный метод. В основу метода положена идея последовательного улучшения некоторого начального ре­шения, путем движения к оптимальному значению целевой функции, которое заранее неизвестно. Для успешного решения задач градиентным методом целесообразно все элементы ре­шения, т. е. искомые х_i, привести к единой шкале путем их нормирования, например

или

Рассмотрим процедуру решения задачи, если целевая функция имеет вид

К = K (х₁, …, x_m) → mах, или K = K (X) → mах.

Выберем начальное решение K(X₀), т.е. исходную точку дви­жения к экстремуму К (X₀) = К (х₁₀, . . ., х_m0).

Выбор начального решения оказывает существенное влия­ние на ход решения задачи и на его успех. Необходимо исполь­зовать всю имеющуюся априорную информацию и физические условия задачи, чтобы как можно удачнее выбрать исходную точку для начала движения к экстремуму.

Найдем градиент функции К (X₀), вычисленный для началь­ной точки решения

Движение к экстремуму производим с определенным ша­гом, т. е. с определенными приращениями переменных. Выбор шага является ответственным этапом в решении. Если вы­брать шаг большим, то можно «перешагнуть» экстремум, а если выбрать шаг малым, то придется долго двигаться к экстремуму. Целесообразно организовать движение с пере­менным шагом, в начале движения применять большой, а за­тем, приближаясь К экстремуму, его уменьшать.

Определим приращение оптимизируемой функции при пер­вом шаге

Значение оптимизируемой функции после первого шага соста­вит К⁽¹⁾(X₁) = К(Х₀) + ΔК⁽¹⁾.

Если К⁽¹⁾(X₁) > K(X₀), до движение происходит в направле­нии экстремума.

Произведем второй шаг. При этом приращение оптимизируе­мой функции будет равняться величине

Если на все время движения значения производных не изменять, т. е. сохранять градиент начального шага, то такой метод поиска экстремума называют методом наискорейшего спуска.

Определим значение целевой функции после второго шага

К⁽²⁾(X₂) = К⁽¹⁾(Х₁) + ΔК⁽²⁾

Если К⁽²⁾(Х₂) > K⁽¹⁾(X₁), то движение происходит по направ­лению к экстремуму.

Продолжаем движение до выполнения условия К^(m)(Х_m) — К^(m-1)(Х_m-1) = 0, или К^(m)(Х_m) — К^(m-1)(Х_m-1) ≤ ξ, где ξ — некоторая окрестность экстремума, удовлетворяющая решение. В точке экстремума ξ = 0.

Рассмотренный алгоритм поиска оптимального значения целевой функции не учитывал ограничений. При решении за­дачи с учетом ограничений используют разновидность гради­ентного метода, называемую методом штрафных функций. Идея метода состоит в переходе к вспомогательной функции R(X), на которую не наложены ограничения R(X)=K(X)+H(X).

Дополнительное слагаемое H(X) отрицательно в задачах максимизации, его называют штрафной функцией. Штрафная функция равна нулю для тех (X), при которых ограничения не нарушаются. Если ограничения нарушаются, то Н(X) — отрицательна.

Штрафную функцию выбирают в виде суммы

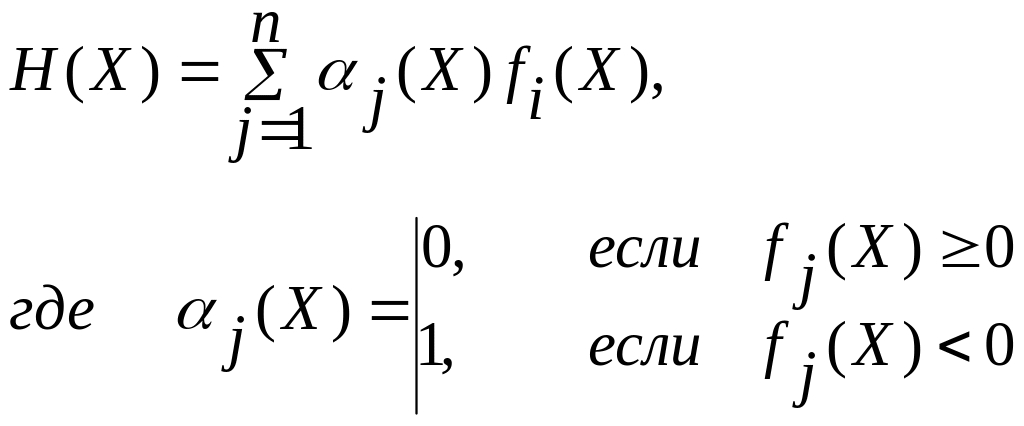
Значение а выбирается достаточным для обеспечения необхо­димой чувствительности, когда наложенные ограничения не вы­полняются,

.

Таким образом, при любом нарушении ограничении резуль­тирующее приращение целевой функции будет отрицательным что указывает на выход решений за допустимую область При' этом «отслеживание» за соблюдением ограничений произвоизводится по всем переменным, т.е. по всем элементам решения от i = 1 до i = m.

Других отличий метод штрафных функций от рассматри­ваемого ранее градиентного метода не имеет

Следует заметить, что при достижении границы области до­пустимых решений целевая функция «отбрасывается» обратно в область, поэтому последующие шаги нужно уменьшать

Градиент функции вычисляется аналогично предыдущем" случаю, а приращения вычисляются по каждой переменной,т.е.

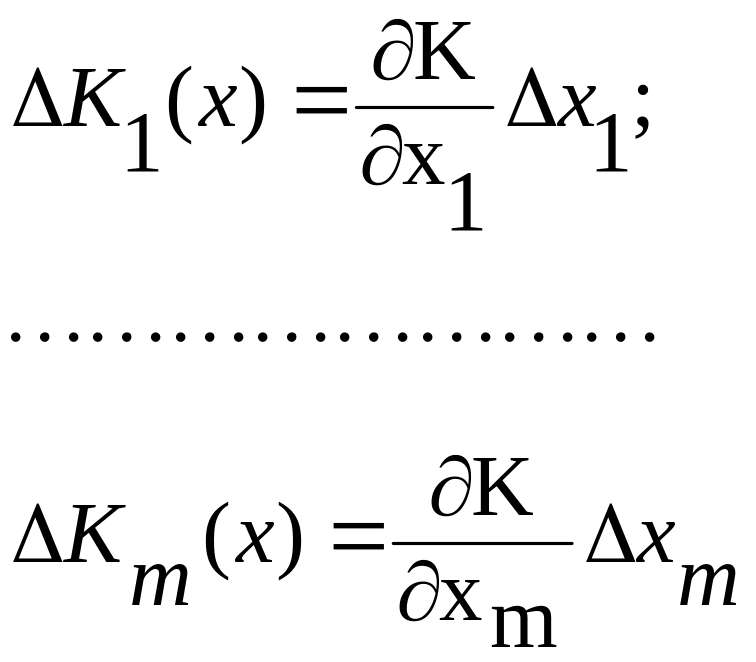
Кроме того, шаг выбирается для всех переменных один и же. Тогда алгоритм вычислений примет вид. При первом шаге

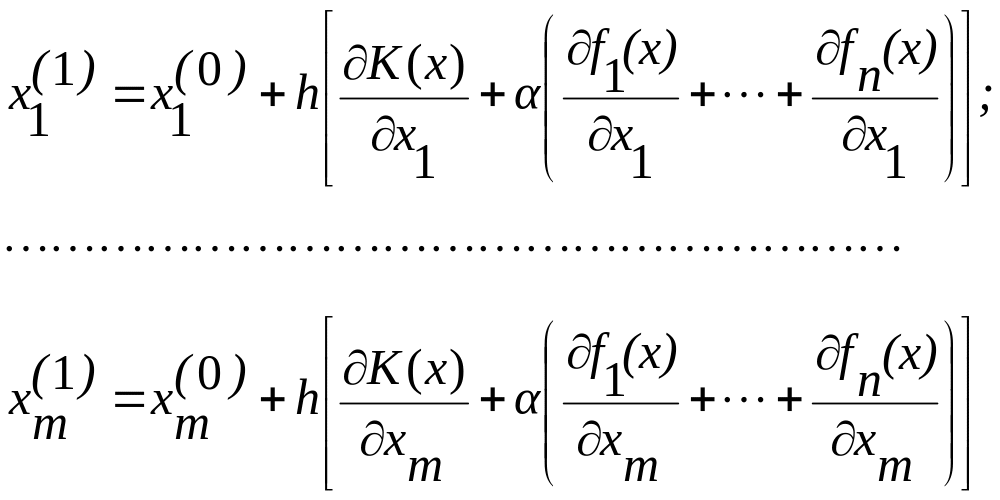
При втором шаге

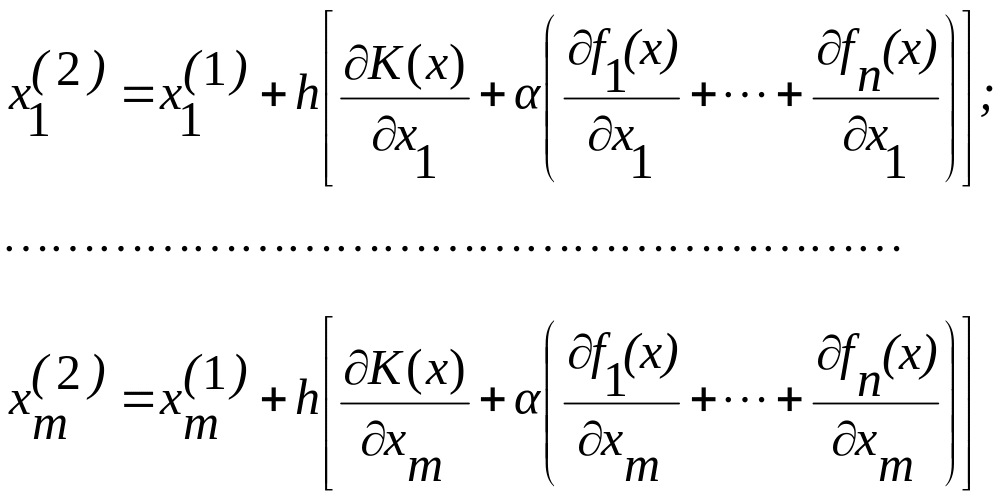
И т. д.

После каждого шага проверяются условия. Если ограни­чения нарушены то появляется значение штрафной функции переменной, которая вышла из области допустимых решений.

Пример. В процессе изготовления изделия используются два вида оборудования с производительностями' x₁ и х₂ — соответ­ственно. Производительность оборудования и показатели ка­чества связаны зависимостями.

Для первого вида оборудования K₁ = x₁ —x₁² для второго вида К₂ = Зx₂ — х₂²

Требуется найти те значения производительности оборудо­вания, которые обеспечивают максимальное значение качества.

Полагая, что результирующий показатель качества является аддитивным, запишем целевую функцию

Известны ограничительные условия

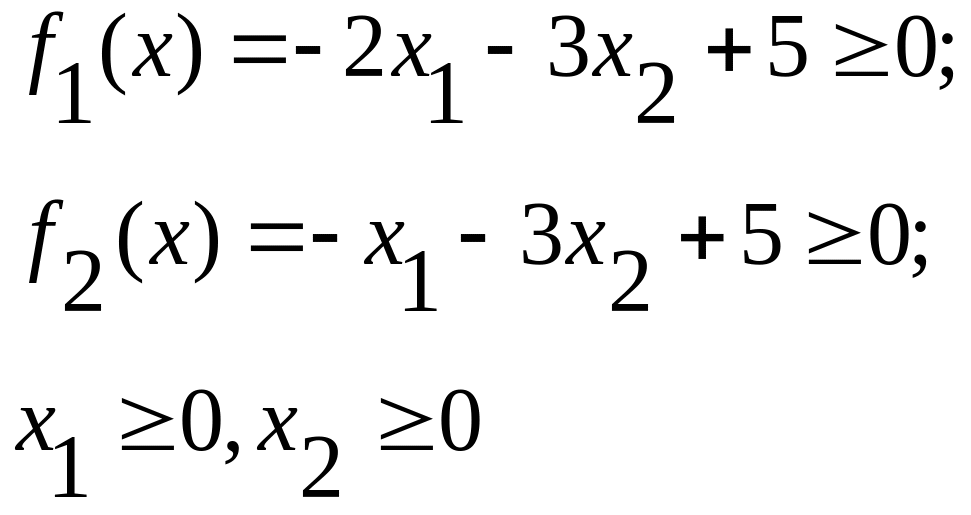
Кроме того, известна допустимая погрешность в определении экстремума ξ = 0,3.

Р е ш е н и е.

Выберем за исходную точку движения x₁ = 0, х₂ = 0, шаг приращения функции h выбираем равным ;, т. е. h = 0,3.

Проверяем выполнимость ограничительных условий. Они выполняются, поэтому α₁⁽⁰⁾ = 0, и, α₂⁽⁰⁾ = 0.

Находим составляющие градиента

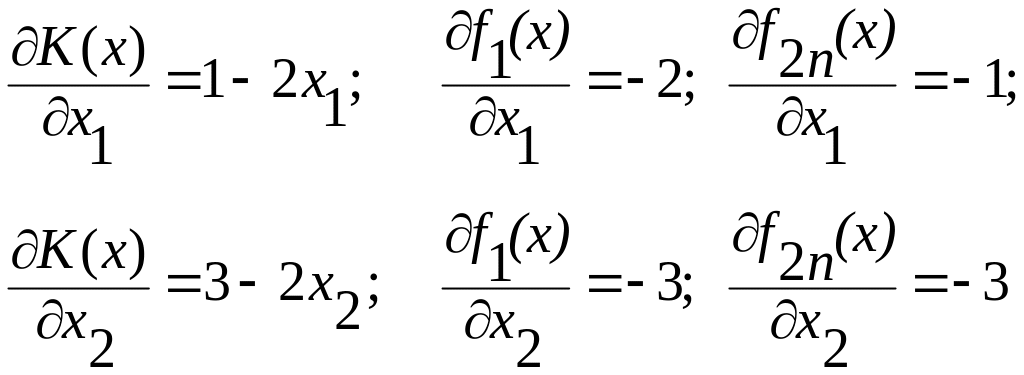
При x₁ = 0, х₂ = 0 имеем K⁽⁰⁾ (x) = 0. Находим значения x₁ и x₂ после первого шага

.

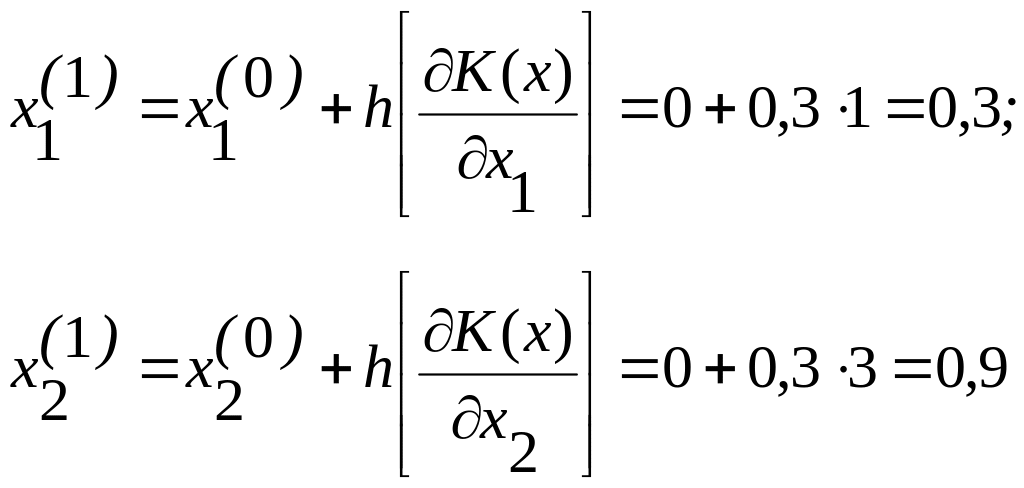Определяем значение целевой функции после первого шага

Следовательно, приращение составляет ΔK⁽¹⁾(x) = 2,1. Заме­чаем, что ΔК⁽¹⁾(х) > ξ поэтому, проверив выполнимость ограни­чений при x₁⁽¹⁾ = 0,3 и x₂⁽¹⁾⁼=0,9, продолжаем движение к экстремуму.

Ограничительные условия выполняются, поэтому а₁⁽¹⁾=0, а₁⁽²⁾=0

Находим значения х₁⁽²⁾ и х₂⁽²⁾.

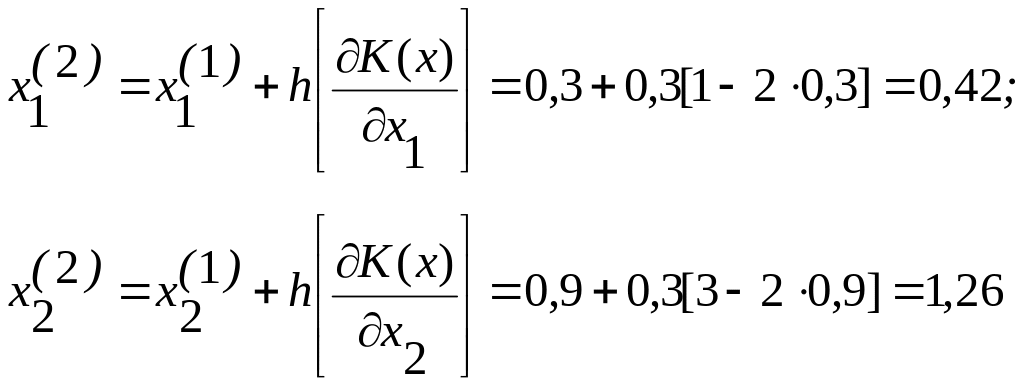
Определим значение целевой функции K⁽²⁾(x):

Находим ΔК⁽²⁾(х)=К⁽²⁾(х)-К⁽¹⁾(х)=2,44—2,1=0,34.

Замечаем, что ΔК⁽²⁾(х)>ξ.

Проверяем выполнимость ограничительных уравнений. Они выполняются, т. е. а₁⁽²⁾=0, а₂⁽²⁾=0.

Делаем следующий шаг и определяем значения x₁⁽³⁾ и x₂⁽¹⁾:

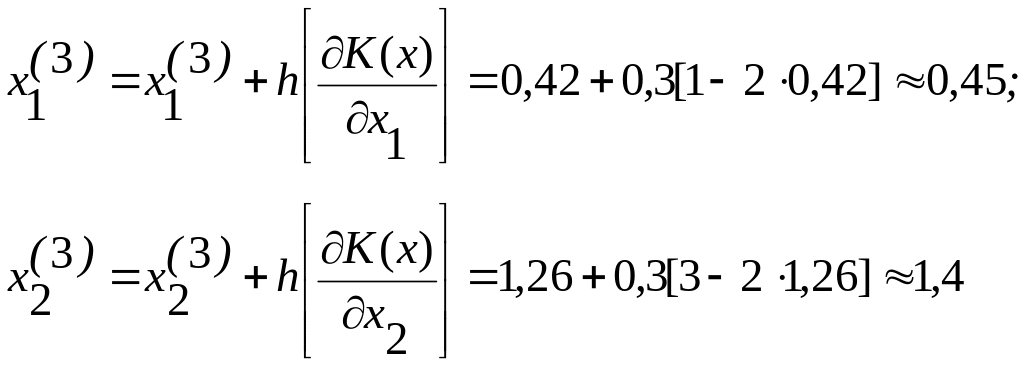
Определяем значение целевой функции после третьего шага cледовательно, ΔК⁽³⁾(х)=0,07, что меньше ξ = 0,3.

Остается проверить выполнимость условий при x₁⁽³⁾=0,45 и x₂⁽³⁾=1,4.

Первое ограничительное условие не выполняется.

Следовательно, α₁⁽³⁾>0.

Для получения искомого решения целесообразно на третьем шаге уменьшить h. Допустим h=0,2, тогда

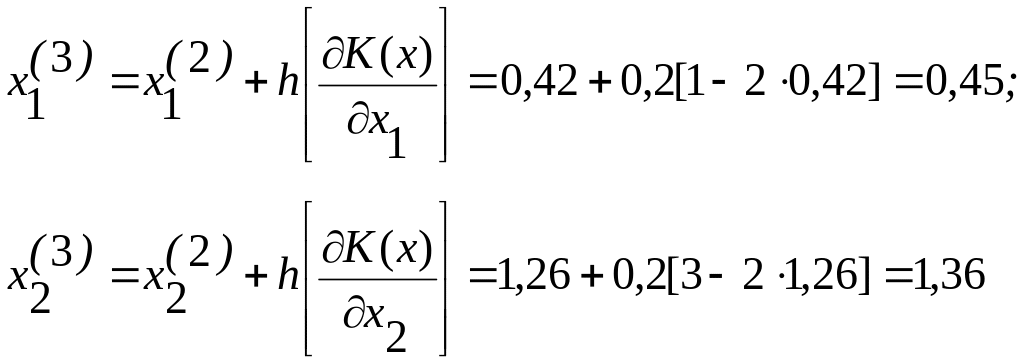
Находим К⁽³⁾(х) с учетом изменения шага. К⁽³⁾(х)=2,65.

Следовательно, К⁽³⁾(х)=0,21. Это меньше ξ=0,3 Снова проверяем ограничительные условия. Они выполняются. Таким образом, задача решена: х₁=0,45, х₂=36, К (х)=2,65.

2. Метод направленного перебора. Этот метод позволяет найти экстремум целевой функции для случая, когда она недифференцируема, или необходимо найти экстремум функ­ции нескольких переменных.

Как и в предыдущем случае, известна целевая функция и ограничения

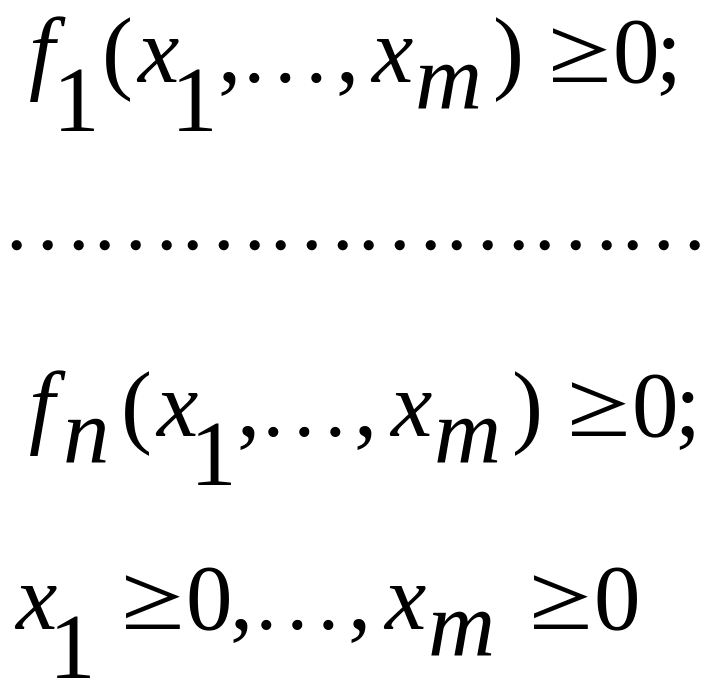
Выберем из физических или экономических соображений некоторую исходную точку К(х₀), удовлетворяющую ограни­чительным уравнениям f_j(x_i), и шаг случайного' поиска h. Поскольку заранее неизвестно предпочтительное направление, в котором целесообразно организовать движение, выбираем одинаковые приращения переменных, каждый раз проверяя выполнение ограничительных уравнений и приращение функ­ции, т. е.

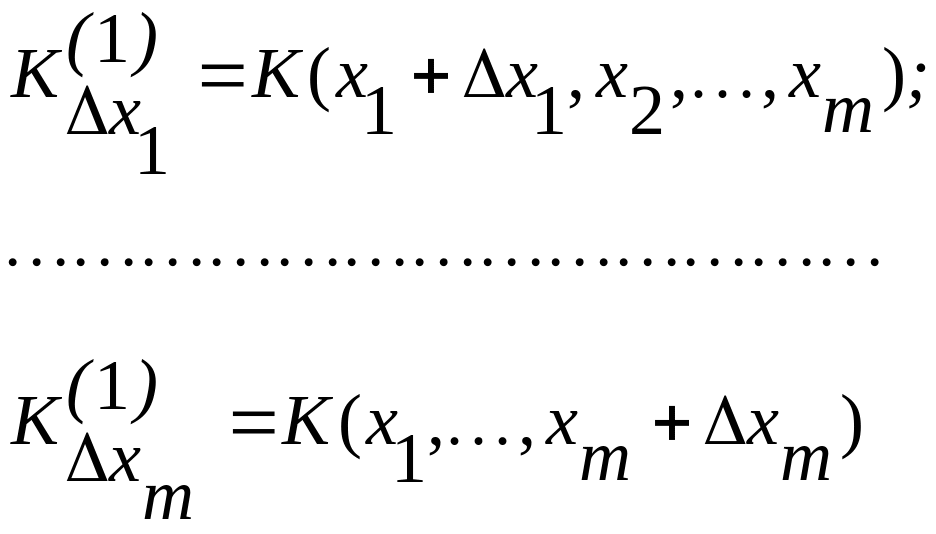
Выбираем те x_i, которые дали наибольшее приращение це­левой функции, затем при втором шаге даем приращения наи­более предпочтительным переменным.

Может иметь место случай, когда некоторым переменным целесообразно давать отрицательные приращения. Такая си­туация складывается, когда исходная точка, вернее исходные координаты, выбраны неудачно. При каждом шаге определя­ется новое значение целевой функции. Оно должно быть боль­ше предыдущего. Поиск продолжают до выполнения условия

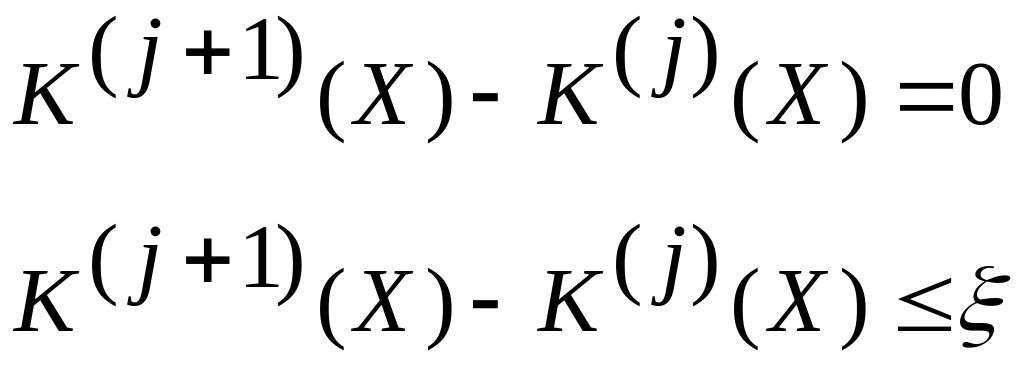
После каждого шага проверяются условия

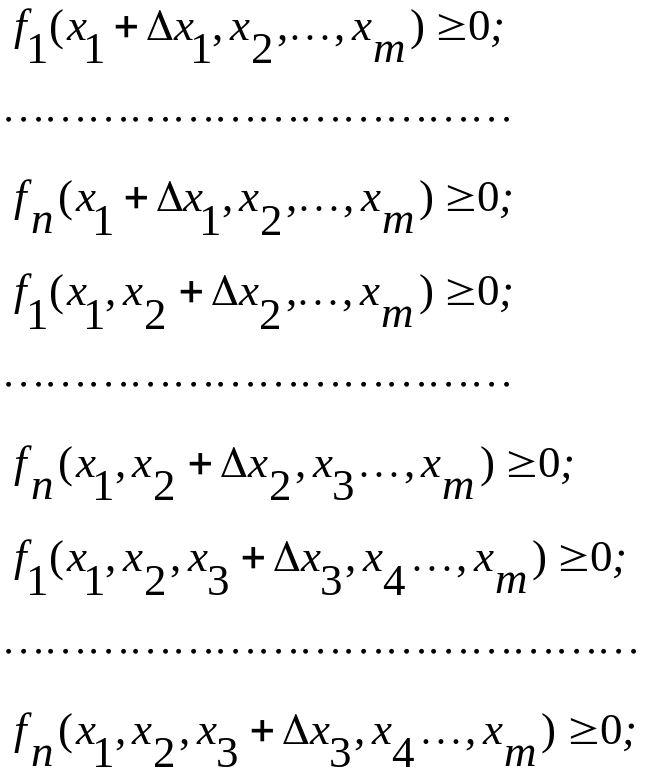
и т.д

3. Метод множителей Лагранжа. Метод является полезным при отыскании оптимальных решений, если целевая функция нелинейна, например, задана некоторым полиномом а ограничения заданы в форме равенств.

Требуется найти максимум целевой функции K=K(x₁,...,...,х_m)→mах. Ограничения заданы в виде

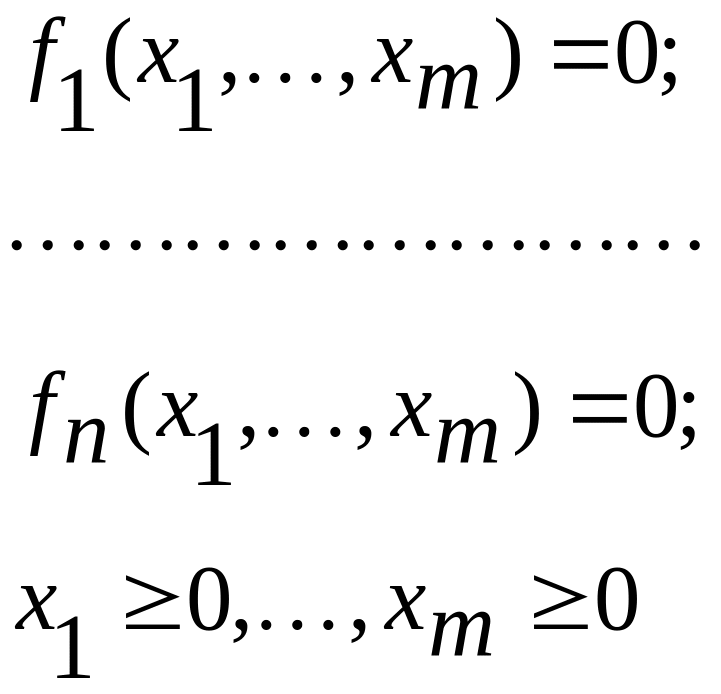
Предполагается, что K(x₁,...,х_m) _и f_j(x₁,...,х_m) дифференцируемы.

Составим функцию Лагранжа

где α_j— неопределенные множители Лагранжа. Количество неизвестных прибавилось, но если мы их найдем и подставим в L то это даст оптимальное решение. Перешли от К к некоторой новой функции L.

Необходимым условием существования экстремума является

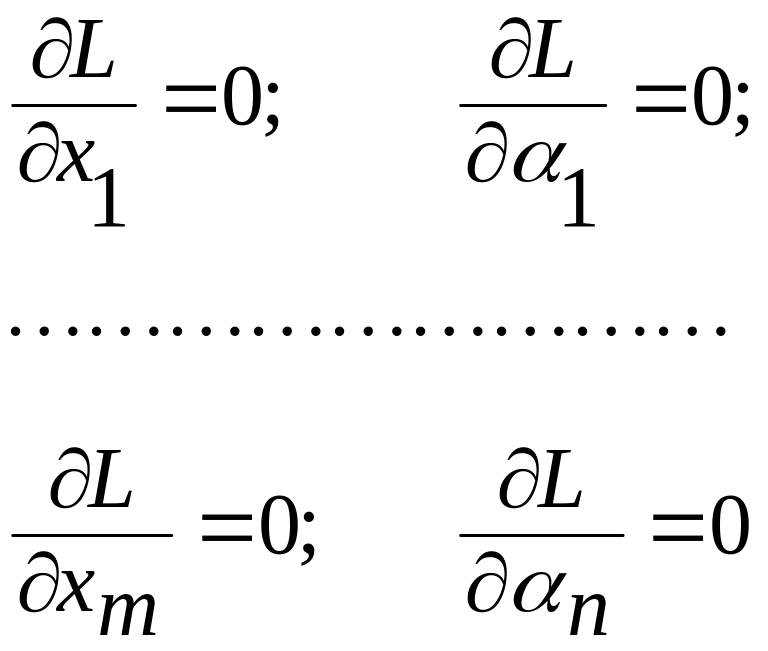
В этой системе столько неизвестных, сколько уравнений. Следо­вательно, можно найти x₁,...,х_m, α₁,...,α_m и, подставив их в функцию Лагранжа, получим оптимальное решение, т. е. L_max.

Пример. Разрабатываемая аппаратура состоит из двух блоков Б₁ и Б₂. Заданная стоимость этих блоков равна соот­ветственно A₁ и А₂. Известен период эксплуатации t и резуль­тирующая интенсивность отказов .

Требуется найти интенсивности отказов блоков, т. с. λ₁ и λ₂, при которой результирующая стоимость использования аппаратуры за время t минимальна, а интенсивность отказов равна заданной, т. е. λ, тогда

Выразим стоимость использования блоков через их надежность

Запишем целевую функцию в форме Лагранжа

(3.6)

Вычислим производные и приравняем их нулю:

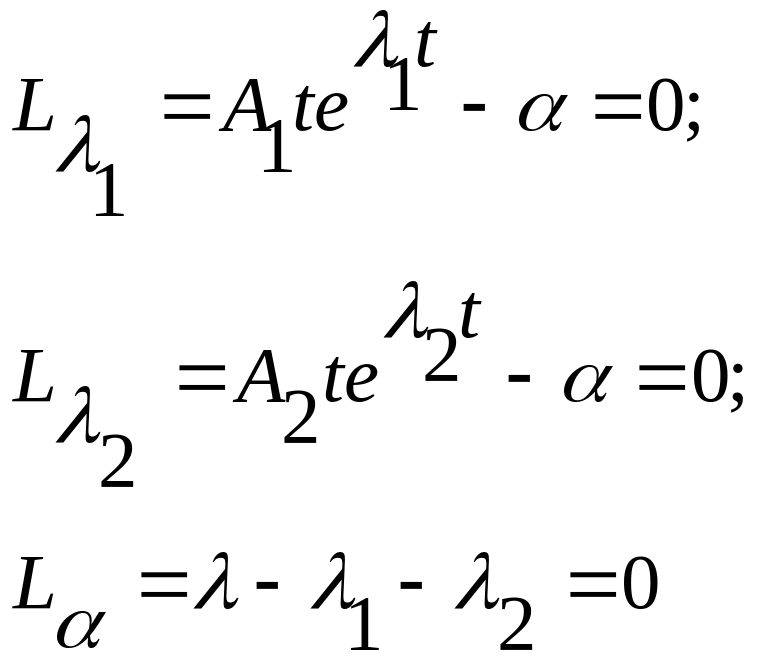
Имеем систему трех уравнений с тремя неизвестными, решив ее, находим λ₁, λ₂, α, подставив их в (3.6), получим оптимальное решение.