3.5. Целочисленное программирование в задачах конструирования

Для многих оптимизационных задач конструирования эле­менты решения должны быть целыми числами, например чис­ло монтажных плат, блоков, модулей, поэтому методы линей­ного программирования, при решении которых может быть получен результат в виде дробей, не удовлетворяют конструк­тора. В этих случаях используют целочисленное программи­рование.

Постановка задачи целочисленного программирования от­личается от линейного программирования тем, что в данном случае на элементы решения наложены условия целочислен-ности.

Существует несколько методов решения задач целочислен­ного "'программирования, однако наибольшее распространение получил метод ветвей и границ. Идея этого метода заключа-ется в том, что сначала решается задача линейного програм­мирования Если получено целочисленное решение, то это и есть искомый результат, а если не получено целочисленное значение элементов решения, то полученный результат счи­тается верхней границей искомого решения. Для достижения целочисленного решения производят ветвление области допу­стимых решений путем введения дополнительных условий задачи.

Постановку задачи целочисленного программирования рас­смотрим на примере из конструкторской практики.

Требуется разработать аппаратуру на основе серийно вы­пускаемых модулей (микросхем) двух типов М₁ и М₂. Извест­но, что без учета резервирования в схеме аппаратуры должно содержаться модулей М₁ не менее b₁, а модулей М₂ — не ме­нее b₂. Кроме того, известно, что выпускаются монтажные платы двух типов П₁ и П₂, которые предполагается использо­вать как конструктивные несущие элементы для разрабаты­ваемой аппаратуры.

Известно также, что в монтажном пространстве платы П₁ может разместиться На монтажной плате П₂ может быть размещено

α₁₂ — модулей М₁; α₂₂ — модулей М₂.

Для каждого типа плат известен весовой коэффициент стоимости, установленный экспертным или каким-либо другим методом.

Для платы П₁ он равен С₁ а для платы П₂—С₂. Требует­ся определить необходимое количество плат для проектирова­ния аппаратуры по типам с условием, чтобы аппаратура обладала максимальным качеством при минимальных затратах.

С учетом условий и требований задачи составим целевую функцию ,

где x₁ — количество плат типа П₁; x₂ — количество плат П₂.

Составим ограничительные уравнения:

x₁ и x₂ — целые числа.

Первое уравнение описывает распределение модулей M₁ среди плат П_i и П₂, а второе уравнение — распределение среди тех же плат, но уже модулей — М₂.

Начнем решение с задачи линейного программирования, преследуя цель получить, если это удастся, целочисленное ре­шение, а если нет, то — верхнюю границу задачи целочислен­ного программирования.

Предположим, что решение найдено с использованием од­ного из известных методов линейного программирования, но при этом целочисленных значений элементов решения не по­лучено,

Наложим дополнительные условия

где х₁^ц — ближайшее целое число к х₁*; x₂^ц—ближайшее целое чис­ло к x₂.

Решаем задачу, разветвив ее на две по х₁^ц и x₂^ц. Вновь решаем задачу линейного программирования с учетом дополнительного условия. Получаем решения х₁** и х₂**. При этом целевая функция имеет значение K**. Если элементы решения являются целыми числами и ограничительные уравнения выполняются, то полу­ченное решение дает оптимальное значение целевой функции.

Если x₁ и x₂ не целые числа, то ветвление продолжают до получения целых чисел или до тех пор, пока ветвление стано­вится невозможным.

Пример. Решим рассмотренную выше задачу при следующих условиях: α₁₁ = 5; α₂₁ = 10; α₁₂ = 10; а₂₂ = 5; b₁ ≥ 80; b₂ ≥ 60; С₁ = 15; С₂ = 20; х₁ ≥ 0, x₂ > 0, x₁x₂ — целые числа.

Решим задачу линейного программирования без учета условий целочисленности х₁ и х₂.

Составим ограничительные уравнения

или

Решение найдем графическим методом. Построим прямые y₁ = 0, у₂ = 0(рис 3.4). Точка соответствует оптимальному решению. При этом x₁ = 2,6; х₂ = 6,6; K = С₁x₁ + С₂x₂ = 15*2_f6 +20*6 6 = 171. Полученное решение не является целочисленным.

Очевидно, целочисленное решение лежит в окрестно­сти точки в области до­пустимых решений. Вероят­нее всего предположить, что оптимальному решениию соответствуют точки 1, 2 или 3.

Рис. 3.4. График, поясняющий решение задач методом целочисленного программирования

Задачу можно решить не прибегая к ее ветвле­нию. Найдем значения це­левой функции для точек 1, 2, 3. То решение являет­ся искомым, для которого целевая функция минималь­на, но не меньше целевой функции, полученной при линейном программировании:

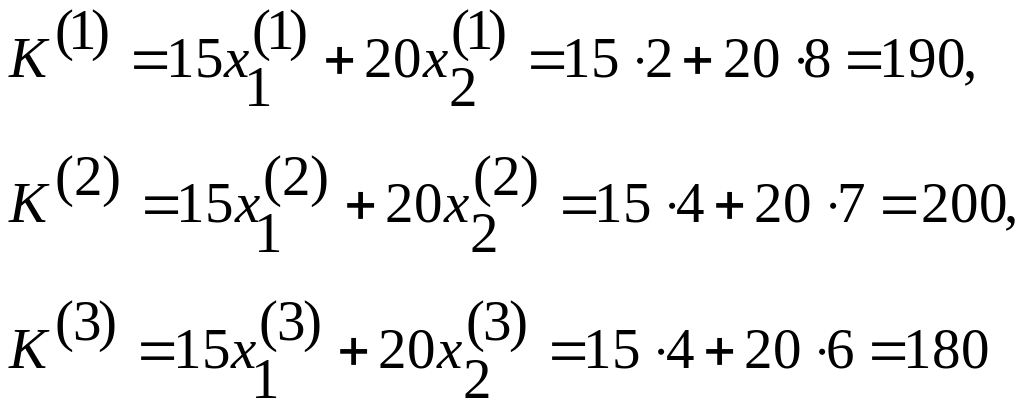
Минимальное значение К⁽³⁾ = 180. Следовательно х₁ = 4; х₂ = 6. При этом К⁽³⁾ == Лmin = 180.