1.7. Обработка результатов контроля качества конструкции

Предположим, что произведены независимые, измерения па­раметров элементов некоторой выборки. В результате измере­ний получена дискретная последовательность значений пара­метров в виде случайных величин x₁,x₂,…,x_n. Требуется про­извести математическую обработку результатов измерений с целью получения числовых характеристик и закона распреде­ления случайной величины х. Приведем примерную последова­тельность обработки результатов измерений.

Целесообразно начать с определения статистического матема­тического ожидания m_х которое равно

Затем составляют таблицу отклонений случайных величин от статистического математического ожидания m_x, Δx_i=x_i — m_х.

Находят квадраты отклонений Δx²_i, а затем определяют ста­тистическую дисперсию

Определяют полуразмахи х_тах — пг_х и т_х— х_т\_п рассеяния слу­чайной величины х относительно статистического математического ожидания. Затем разбивают полуразмахи х_max—m_х и m_х — х_min на 10 — 20 одинаковых интервалов (разрядов) ΔN с целью пост­роения гистограммы. Иногда для вычисления числа разрядов N используют формулу N=1+3,3Inn.

Определяют количество попаданий случайных значений x_i в каждый из разрядов N_j после чего вычисляют статистические частоты f_i попадания случайной величины х в каждый из разря­дов f_j=N_j/n.

После этого переходят к построению гистограммы, пред­ставляющей собой статистическую плотность распределения дискретных значений случайной величины х (рис. 1.16).

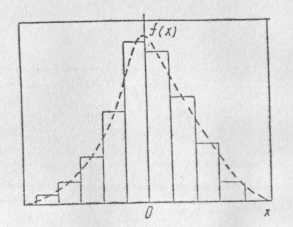
Рис. 1.16. Гистограмма и функ­ция плотности

Каждая из площадей прямоуголь­ников, образованных величиной раз­ряда ΔN_j и статистической частотой f_j, представляет собой статистическую вероятность попадания случайной величины в j-й разряд, Р_j=f_jΔN_j. Суммируя площади прямоугольников гистограммы, получают эмпириче­ский закон (рис. 1.17) вероятности для случайной величины х.

Затем находят закон, описыва­ющий полученную зависимость F*(x)+ При этом подбирают один из наиболее близких по виду тео-

ретических законов распределения вероятностей к полученному эмпирическому (статистическому) закону. Оценивают согласо­ванность теоретического и статистического законов. Для этой цели используют критерии согласия, например, критерий А. Н. Колмогорова, Н. В. Смирнова или Пирсона.

Все критерии согласия построены по одной схеме. Выбирает­ся некоторый параметр в качестве меры расхождения эмпири­ческого и теоретического законов. Этот параметр не должен зависеть от проверяемого закона, он должен быть прост и достаточно чувствителен к отклонению статистического закона от теоретического.

Рассмотрим некоторые из критериев согласия и методику их использования при обработке результатов измерений.

Критерий А. Н. Колмогорова. Этот критерий при­меняют для случая, когда число элементов выборки достаточно велико, обычно двадцать и более. Рассматривают две функции. Одна из них является функцией, описывающей теоретический закон, а вторая — эмпирический, т. е. F(x) и F*[x). В качестве меры рассогласования законов принимают максимальное зна­чение (по модулю) разности

А. Н. Колмогоров доказал, что для любой функции при неограниченном возрастании числа независимых наблюдений п существует вероятность выполнения неравенства

(1.11)

где Q(λ) — вероятность несогласования; λ — число, заключенное между нулем и двумя, т.е. 2 > λ > 0; α — уровень значимости,' обычно α > 0,3. А. Н. Колмогоров построил таблицу значений Q(λ) и соответствующих им значений л (табл 1. приложения).

Оценку согласованности законов производят следующим обра­зом. На одном графике строят теоретический и эмпирический законы (рис. 1.18) и по графику находят ΔF_max, после чего опре­деляют λ=ΔF_max√n.

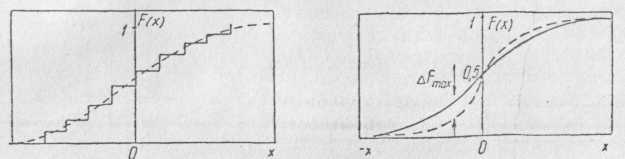
Рис. 1.17. График функции вероятности

Рис. 1.18. График, поясняющий использование критерия согласия Колмогорова

Для найденного значения λ по табл. 1 приложения подбирают соответствующее значение Q(λ), после чего определяют α=1-Q(λ).

Если α > 0,3, то согласованность считают достаточной.

Пример. Произведены измерения параметров элементов выборки n=25. После построения теоретического и эмпирического законов наибольшее значение ΔF_msx составило 0,2. Определить согласие законов.

Решен и е. Находим λ

Из табл. 1 приложения находим значение Q(λ)=0,8. Определяем α=1—Q(λ)=0,2. В данном случае α<0,3, следователь­но, согласованность законов слабая.

Критерий Н. В. Смирнова. Этот критерий был пред­ложен для проверки предположения о принадлежности двух выборок одной генеральной совокупности.

Предположим, что произведено n₁ независимых измерений выборки х и n₂ независимых измерений выборки у. В результате обработки данных получены две эмпирические функции F*(х) и F*(y). Максимальное рассогласование этих функций по модулю

Н. В. Смирнов установил, что случайная величина

(1.12)

удовлетворяет закону Q(λ), установленному А. Н. Колмогоровым при n₁→∞ и n₂→∞.

Определив λ находят по таблице А. Н. Колмогорова соот­ветствующее значение Q(λ), а затем определяют α, т. е. уровень значимости. Если α>0,3, то предположение о принадлежности двух выборок одной генеральной совокупности подтверждается.

Пример Произведены независимые измерения параметров элементов двух выборок n₁=n₂=100. После обработки резуль­татов изменений определено значение ΔF_msx=0.1. Требуется подтвердить предположение о при­надлежности двух выборок од­ной генеральной совокупности.

Решение. Находим

Из таблицы (приложение П. 1) находим Q(λ)=0,3, а затем α=1-Q(λ)=0,7. Следователь­но, гипотеза о принадлежности двух выборок одной генеральной совокупности подтверждается.

Критерий Пирсона. Для этого ; критерия за меру рас­согласования принимают χ², значение этой величины находят из равенства

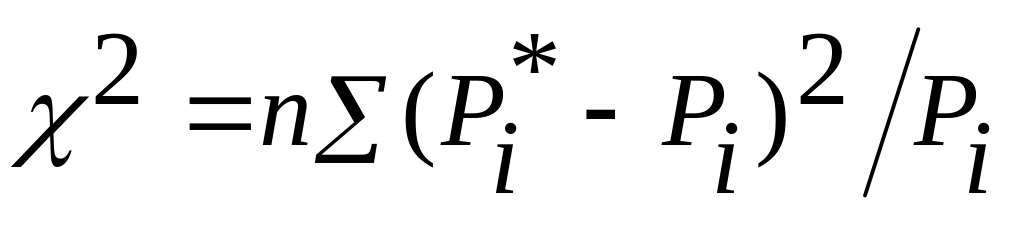
_Где n - объем выборки; Р*_t — эмпирическая вероятность попадании случайной величины в i-й разряд (рис. 1.19); Р_i — теоретическое значение вероятности для иго разряда (рис. 1.19); N—число разрядов, на которое разбит размах выборки.

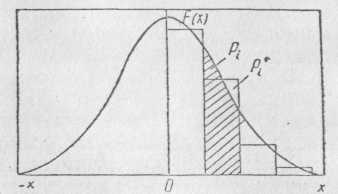
Рис. 1.19. График, поясняющий кри­терий согласия Пирсона

Для χ² составлена табл. 2 приложения, где ее значения соответ­ствуют определенным уровням значимости а и числу степеней свободы К, K=N-r-1, где r —число параметров выбранного закона.

Для нормального закона число параметров равно двум, Это σ и m, т.е. среднее квадратическое отклонение и математическое ожидание.

По формуле (1.13) определяют значение χ² и сравнивают его с табличным значением χ². Если χ²_табл>χ², то согласие считается удовлетворительным.

Заметим, что этот критерий применяют для определения согласия законов при малых объемах выборок, обычно n≤25.

Рассмотренный метод обработки результатов контроля качества пригоден для классического эксперимента. Однако в по­следние годы большое внимание уделяется многофакторному эксперименту, который находит все более широкое распростра­нение и применение в практике.

Эксперимент стал играть активную роль в процессе констру­ирования аппаратуры. С его помощью вскрываются взаимосвя­зи, ранее не известные разработчику. Он позволяет восполнить недостающую информацию и уточнить отдельные теоретические положения, выдвигаемые при проектировании и, наконец, экс­перимент является практической проверкой показателей каче­ства разработанной аппаратуры.

До недавнего времени эксперимент в основном применялся при испытаниях и был инструментом анализа. В настоящее время его роль возросла и он стал использоваться при синтезе аппаратуры.

В процессе инженерного эксперимента могут иметь место Два плана: эксперимент классического или последовательного плана и эксперимент случайного или рандомизированного пла­на, зачастую называемый факторным экспериментом.

При последовательном эксперименте задают некоторые зна­чения варьируемому параметру, т. е. аргументу и отслеживают значения функции. Обычно изменение аргумента производится от минимального значения до его максимального значения с равными интервалами. Однако, последовательный эксперимент может строиться по иной схеме, когда задают равные или оди­наковые приращения функции при произвольных значениях ар­гумента.

Наиболее сложным вопросом при последовательном экспе­рименте является выбор шага изменения аргумента, так как от его правильного выбора в значительной степени зависит точ­ность результата, т. е. точность определения функции. При по­следовательном эксперименте побочные (случайные) факторы не учитываются.

В процессе проведения факторного эксперимента влияние побочных факторов не исключается, око учитывается путем варьирования всеми факторами, т. е. путем введения рандоми­зации. Рассмотрим принцип рандомизации на примере [19].

Необходимо проверить эффективность нового инструмента, например, резца. В данном случае зависимой переменной, т. е. функцией является продукция, а независимой переменной — скорость резания. В этом эксперименте имеется еще одна переменная—это рабочий. Для проведения эксперимента нужен некоторый «средний» рабочий. Выберем случайным образом четырех рабочих и четыре скорости резания, включая макси­мальную и минимальную. Построим эксперимент так, чтобы каждый рабочий смог поработать на каждой скорости резания хотя бы один день. План эксперимента может быть представ­лен табл. 1.3.

Такой план является несовершенным, в нем не учтен фактор натренированности рабочего и ослабление его внимания. Ины­ми словами, в [данном случае не произведена рандомизация

рабочего дня.

Скорость резания на каждый день рабочий выбирает по жребию. В этом случае план эксперимента может быть пред­ставлен табл. 1.4.

Таблица 1.3

Рабочий	Дни недели и скорости реза и и я
	Поне­дель­ник	Втор­ник	Среда	Чет­верг
А	4	2	1	3
Б	2	3	4	1
В	3	1	2	4
Г	1	4	3	о

Таблица 1.4

рабочий	Дни недели и скорости резания
	Понедел­ник	Втор­ник	Среда	Четверг
А	1	2	3	4
Б	1	2	3	4
В	1	2	3	4
Г	1	2	4	4

Такой план называют латинским квадратом 4X4. Здесь выступают четыре фактора или, как принято говорить в теории эксперимента, четыре уровня: скорость резания, различные рабочие, различные дни недели и жребий при выборе скорости резания.

Если уровень шесть, то квадрат должен иметь 6X6 факторов.

Это уже вызывает сложности, поэтому используют греко-латинский квадрат 3x3, т. е. берут блоки, каждый из которых содержит по 3X3 факторов из квадрата 6x6 факторов.

Перейдем к некоторым количественным показателям, исполь­зуемым при рандомизированном эксперименте. Полагаем, что план эксперимента полностью рандомизируется. Эксперимент ставится таким образом, чтобы варьировались все факторы одновременно. При этом увеличивается точность статистической оценки изучаемого явления.

Для обработки экспериментальных данных используется дисперсионный анализ, позволяющий проверить гипотезу о на­личии эффекта, вносимого исследуемым фактором, путем выде­ления и сравнения двух дисперсий: дисперсии, характеризующей изменение уровней исследуемого фактора; дисперсии, характеризующей рассеяние, связанное с ошибкой эксперимента.

Пример. Исследуем влияние положения платы на резуль­тат испытания ее динамических свойств на вибрирующем осно­вании. Рассмотрим влияние одного из факторов — положение платы на столе вибростенда. Будем располагать плату в трех положениях. Одно положение от другого отличается поворотом платы на вибрирующем основании на 120° (рис. 1.20).

Рис. 1.2.0. Схема расположения монтажных плат на вибрирующем осно­вании

Наряду с исследуемым фактором проявляются и другие факторы, например: влияние различных партий плат, временная нестабильность процесса измерений ииспытаний, возможные индивидуальные погрешности, вносимые разными операторами.

Выделим на этом фоне случайных явлений главный фа ктор — положение платы.

Предположим, что доста­точной будет выборка, состоя­щая из шести плат, проверяе­мых шестью операторами в те­чении шести дней.

Для организации выборки воспользуемся таблицей слу­чайных чисел. Возьмем из таб­лицы подряд те числа, у кото­рых две последние цифры имеют предел 1—6. Первая цифра будет обозначать номер платы, а вторая — номер дня испытания. Составим план эксперимента в виде табл. 1.5.

Вычислим суммарное значение измеренных амплитуд вибрации для каждого уровня n

Вычислим среднее значение суммарных амплитуд вибрации по уровням

где К = 3.

Оценим влияние уровней

Вычислим математическое ожидание амплитуд вибрации

Следовательно, амплитуда вибрации с учетом влияния /-го уров­ня составит

где ξ— инструментальная погрешность; ΔY_j — погрешность, вно­симая j-м уровнем.

Т а бл и ца 1.5

Номер оператора, n	Положение платы
	уровень А		уровень В		уровет С
	А	YА	В	Yв	С	YC
1	6/6	YA1	6/1	YB1	3/6	YC1
2	4/1	YА2	6/2	YB2	2/6	YC2
3	5/1	YА3	2/5	YB3	1/4	YC3
4	3/5	Yа4	2/4	YB4	5/3	YC4
5	2/5	Yа5	3/3	YB5	3/6	YC5
6	1/3	Yа6	3/6	YB6	3/5	YC6
		YАΣ		YBΣ		YCΣ

Вычислим математические ожидания амплитуд вибрации для каждого из уровней,

Определим дисперсии для каждого уровня

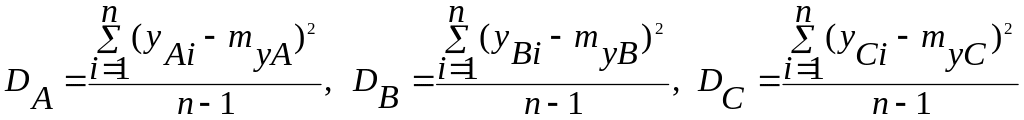
Вычислим дисперсию по всему ансамблю измерений

Сравним дисперсии, полученные для уровней, с дисперсией всего ансамбля измерений

Полученные значения ΔD, позволяют судить о влиянии уров­ней, т.е. о наличии или отсутствии фактора—положения платы.