2.2. Линеаризация дифференциальных уравнений

систем с параметрическим регулятором

Р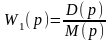 ешение дифференциальных уравнений систем ССР с параметрическим регулятором скорости резания, содержащим делительное звено ДЗ, т.е. ПР, АППР и ПДС систем ССР (см. соответственно рис. I.I2 -.1.14) можно приближённо найти, используя линеаризацию этих уравнений при разрешении их относительно радиуса обработки [66]. Рассмотрим ПДС (АППР) систему ССР, приняв что передаточные функции W₁(p), W₂(р) представляют собой дробно-рациональные функции степенных многочленов D(р) , М(р), Р(р)» Q(p) аргумента р, причём порядок их числителей не превосходит порядка соответствующих знаменателей

(2.8)

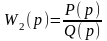
(2.9)

У гловая скорость шпинделя при этом на основании (1.70) равна

(2.10)

или, приняв во внимание (1.40)

. (2.11)

П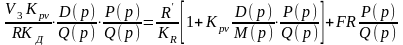 реобразуем это выражение к виду

(2.12)

Д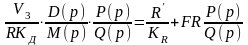 ля ПР системы ССР в соответствии с (1.62) при передаточных функциях W₁(p), W₂(p) , описывающихся (2.8), (2.9) и с учётом (1.40), можно записать

. (2.13)

Сравнение (2.12) и (2.13) показывает, что они принципиально не отличаются и последнее уравнение практически является частным случаем (2.12), поэтому дальнейшее рассмотрение будем проводить на примере выражения (2.12). Линеаризация этого уравнения возможна, как это будет показано в дальнейшем, если в его левой части при приведении к общему знаменателю будут отсутствовать члены, содержащие аргумент р. Это возможно при F= 0 в следующих случаях

D (p)=K₁

W₂(p)=K₂ (2.14)

P(p)=K₂

W₁(p)=K₁ (2.15)

D(p)=K₁

P(p)=KM(p) (2.16)

P(p)=K₂

Q(p)=KD(p) (2.17)

где К - коэффициент,

D(p)=K₁ (2.18)

P(p)=K₂

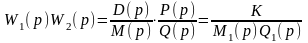(2.19)

где M₁(p), Q₁(p) - степенные многочлены аргумента р.

Во всех указанных случаях линеаризация (2.12) проводится одним и тем же образом рассмотрим это, например, при выполнении (2.16), с учётом которого уравнение (2.12) принимает

(2.20)

Принимая

Q(p) = a_sp^S+a_S-1(p^S-1+ ... + a₁p +a₀ , (2.21)

где a_s… a₀ - коэффициенты многочлена Q(p) степени S получаем

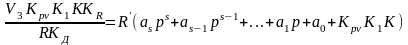
или

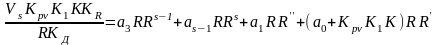. (2.22)

Запишем далее

( R²)'=2RR

(R²)''=2RR''+2(R')²

(R²)'''=2RR'''+6R'R'''

(2.23)

Считая, что значение производных по R меньше самого радиуса, можно пренебречь в (2.23) вследствие малости слагаемыми, содержащими произведения производных. Подставляя при этом из (2.23) в (2.22) RR^(S+1), RR^s,…, RR' получим

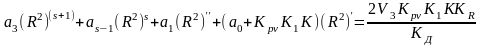(2.24)

Обозначив в этом выражении R²=y, запишем уравнение

(2.25)

которое относительно y является линейным дифференциальным уравнением с постоянными коэффициентами.

В случае F=const≠0 линеаризация (2.12) проводится при выполнении (2.14) – (2.16), (2.18) аналогичным рассмотренному выше образом. Так, с учётом (2.16) уравнение (2.12) принимает вид

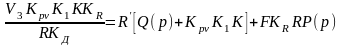(2.26)

Приняв

P(p)=b_npⁿ+b_n-1p^n-1+…+b₁p+b₀ , (2.27)

где b_n…b₀- коэффициенты многочлена P(p) степени n и с учётом (2.21) получим

(2.28)

Откуда находим

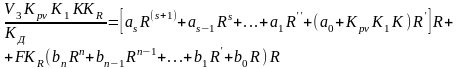(2.29) Подставляя в последнее выражение из (2.23) R R^(s+1) , RR^s, пренебрегая, как и ранее, слагаемыми, содержащими произведения производных, выполнив замену R² = y и, приняв, что S > n , запишем

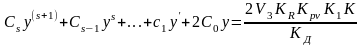(2.30)

где С_S ... С₀ - коэффициенты многочлена степени S, образованные коэффициентами а₃... a_0, b_n…b_{0 ,} K_R ,F.

Уравнение (2.30) также является линейным дифференциальным уравнением.

Необходимо отметить, что при выполнении других соответствующих условий, линеаризация дифференциальных уравнений систем ССР с ДЗ происходит описанным выше образом и они принимают вид, аналогичный (2.25), (2.30).

В том случае, когда механизм поперечного перемещения суппорта станка имеет автономный электропривод с передаточ ной функцией W_n(p)=N(p)/ Ψ(p), где N(р), Ψ(p)- степенные многочлены аргумента р и с учётом того, что

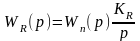, (2.31)

можно записать, например, для ПДС или АППР системы ССР в соответствии с (1.70) следующее выражение

(2.32)

Это уравнение также возможно линеаризовать, если при приведении к общему знаменателю в его левой части будут отсутствовать члены, содержащие аргумент р.

Однако, как правило, нет необходимости в учёте переходной функции W_n(р) привода поперечной подачи, поскольку в сиcтемах ССР её постоянные времени много меньше постоянных времени передаточных функций главного привода и функции W_R(p), поэтому функция W_n(p) не оказывает существенного влияния на процессы в системах ССР.