3.3. Динамика систем с дискретным

измерением радиуса обработки

Динамические процессы в дискретных как и в непрерывных системах ССР обусловлены действием V₃ , когда система движется до установившегося значения V при отсутствии возмущающего воздействия (F=0), появлением возмущающего воздействия (F=Const) в момент врезания при установившемся значении V, а также дискретизацией радиуса в процессе работы системы, т.е. изменением значения R_N.

Найдём выражения, определяющие поведение координат дискретных систем ССР в динамических режимах. Подставив в (3.13) значения W₁(p), W₂(p), U₀ из (1.28), (1.29), (1.54), запишем для АПР системы ССР следующее уравнение

, (3.41)

с учётом (1.40) это выражение примет вид

, (3.42)

Обозначив на каждом уровне N корни однородного уравнения, соответствующего уравнению (3.42) , частное решение (3.42) –B, а постоянные интегрирования – С_1N , С_2N , C_3N, запишем решение (3.42) в виде

, (3.43)

. (3.44)

Постоянные интегрирования определяются на каждом уровне N при t=0. В соответствии с методом припасовывания [53,137] начальными значениями уровня N, т.е. значения R_N (0) и его производных, являются конечные значения уровня N_-1 , найденные в момент времени t_N , когда

R_N-1(t_N)=R_N. Первая производная R_Nv(t) радиуса по времени и вторая –

R_NU (t) равны

(3.45)

(3.46)

Постоянные интегрирования С_1N , C_2N , C_3N находим из следующих уравнений

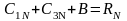
(3.47)

где R(_N-1)v – значение первой производной радиуса в конце (N-1) уровня дискретизации;

R(_N-1)u– значение второй производной радиуса в конце (N-1) уровня дискретизации.

Откуда находим

, (3.48)

(3.49)

. (3.50)

Поскольку по требованиям технологии обработка изделии должна начинаться, когда шпиндель вращается с заданной скоростью и все процессы в системе установились, то в начале уровня N=0 угловая скорость имеет заданное значение, а R_N=R_д. При этом в выражениях (3.47) – (3.50) необходимо принять R_N=R_д, R_(N-1)V=V₃K_R/R_д, R_(N-1)U=0.

Угловая скорость w_N (t) в данном случае на основании (1.40)

. (3.51)

Исследование динамических процессов в АПР системе ССР можно упростить, допустив, что к моменту перехода на следующий уровень .дискретизации процессы в системе установились и уровень N процессы в системе установились и описываются выражениями (3.14), (3.15). При этом с учетом (1.40)

(3.52)

. (3.53)

Для ПДС и АППР систем ССР с учётом W₁(p), W₂(p), K_Д, описывающихся (1.28), (1.29), (1.71), на основании (3.26) получим

(3.54)

На рис. 3.9, 3.10 показаны переходные функции по w_N и V_N в рассматриваемых системах ССР, значение параметров которых определяется (1.77).Здесь необходимо отметить, что в пусковом режиме, т.е. при N=0 переходные функции в ПДС и АППР системах могут быть улучшены и иметь максимальное перерегулирование не более 3 – 4 % за счёт снижения в этом режиме значения К_рv, так как это делалось для непрерывных систем.

В том случае, когда F=0 или весьма близко к этому значению, например, при холостом ходе станка или обработке с малыми усилиями резания, выражение (З_.42) принимает вид

(3.59)

Откуда при комплексно-сопряжённых корнях характеристического уравнения получаем

(3.60)

(3.61)

(3.63)

(3.64)

Производные радиуса по времени равны (3.64)

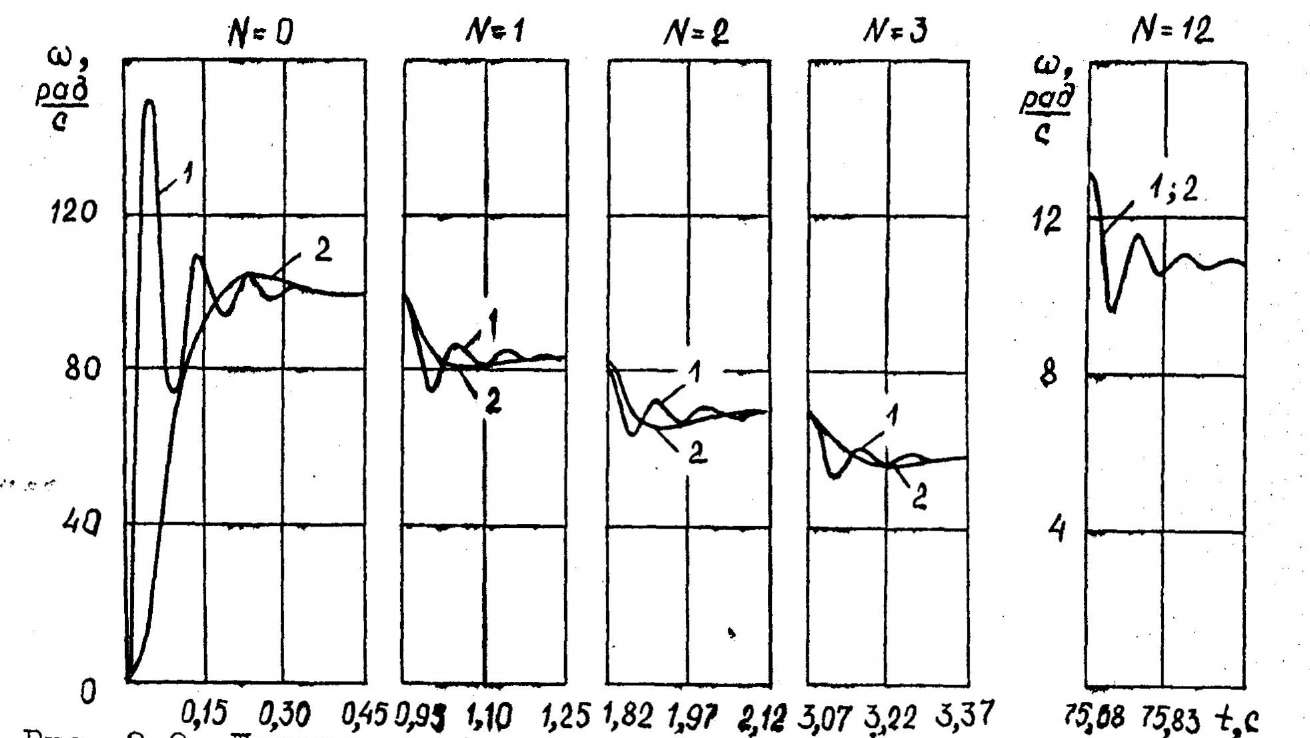
Pис. 3.9. Переходные функции систем ССР по угловой скорости шпинделя при V₃ = 2 м/с, , R_д=20мм, K_R=0,08мм/рад, F=100Н. Кривая 1 в ПДС и АППР системе при К_рv=6; кривая 2 - в АПР системе при K_pv =22.

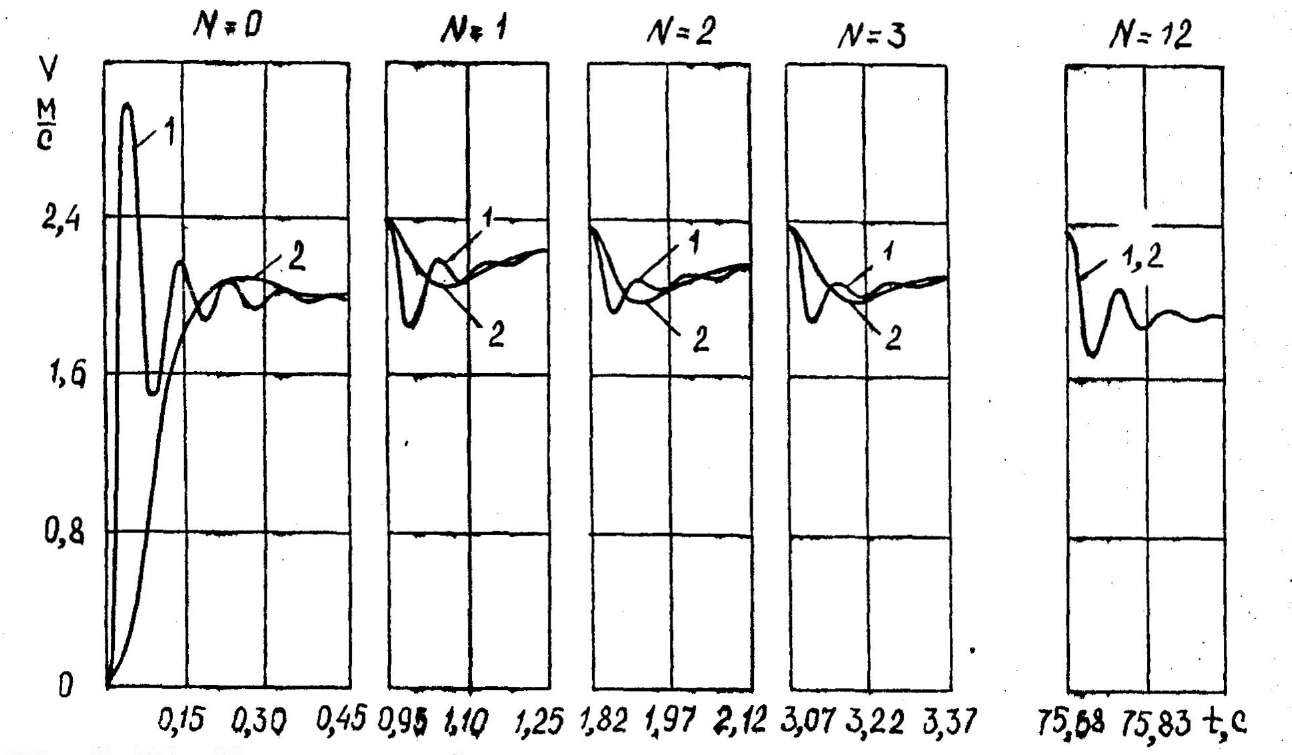
Рис.3.10. Переходные функции систем ССР по скорости резания при V₃ = 2м/с, , R_д=20мм, K_R=0,08мм/рад, F=100Н. Кривая I - в ПДС и АППР системе при К_рv=6; кривая 2 - в АПР системе при K_pv=22.

(3.65)

П остоянные интегрирования C_1N, C_2N и коэффициент B_N определяются из уравнений, аналогичных (3.47), т.е.

(3.66)

откуда получаем

(3.67)

(3.68)

, (3.69)

а угловая скорость w_N(t) находится согласно (3.51).

Для этого случая (F⁼0) при выполнении (3.52), (3.53) на основании (3.67) и последнего уравнения (3.66), получим

(3.70)

(3.71)

Подставив в (3.60) полученные значения, преобразуем его к виду

. (3.72)

На основании (3.51), (3.72) запишем

(3.73)

В ПДС и АППP системах ССР при F = 0 на основании (3.54) имеем

(3.74)

Если характеристическое уравнение, соответствующее (3.74), имеет комплексно-сопряжённые корни , то R_N(t) в ПДС и АППР системах ССР описывается (3.60) с теми же значениями α, A_N, B_N, C_1N, C_2N, но при другом β, котрое не зависит от R_N и равно

(3.75)

В случае выполнения (3.57), (3.58) для рассматриваемых систем имеем

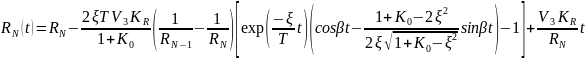(3.76)

(3.77)

Зависимость скорости резания V_N(t) от времени находится в рассматриваемых случаях в соответствии с (3.35), принимая во внимание, что угловая скорость при этом является функцией времени и описывается (3.73), (3.73).

Анализ переходных функций систем ССР показывает, что при дискретном измерении R при прочих равных условиях лучшими динамическими характеристиками обладает АПР система, особенно при малых значениях N, с увеличением которого динамика системы ухудшается, приближаясь к динамике ПДС (АППР) системы, и становится равной ей при максимальных значениях N. Необходимо так же отметить, что в дискретных системах ССР зависимость динамических процессов от технологических параметров процесса резания имеет гораздо меньше значение, чем в непрерывных системах.