25. Модель эк.Роста домара

Время t изменяется дискретно. Модель описывает динамику дохода Y(t). Должно выполняться следующее соотношение:

Y_c(t+1)+Y_c(t)=Y(t+1)+Y(t), где Y_c – совокупный доход, Y – национальный доход

Y(t+1)+Y(t)=q*I(t), где I(t) – чистые производственные инвестиции, q – прирост национального дохода на единицу инвестиций.

Реальный прирост национального дохода несколько меньше, чем q*I(t), т.к. ввод новых производств может привести к сокращению производства на старых объектах, т.е. Y (t +1)+Y(t)=δ*I(t), где 0<δ<1

Y_c(t +1)=c*Y_c(t +1)+I(t+1)+Y_o+I_o , где с – норма сбережения

Y_c(t)=c*Y_c(t)+I(t)+Y_o+I_o

Y_c(t +1)– Y_c(t)=с(Y_c(t +1)– Y_c(t))+I(t+1)–I(t)

(1–с)(Y_c(t +1) – Y_c(t))=I(t+1)–I(t).

1–с=s (предельная норма сбережения)

s*(Y_c(t+1)–Y_c(t))=I(t+1)–I(t)

Таким образом, прирост национального дохода:

Темпа прироста инвестиций:

Темп прироста национального дохода равен темпу прироста инвестиций:

Связь между национальнам доходом в году t+1 и t:

26. Модель эк.Роста харрода

Основное предположение модели:

– некоторое число, причем в зависимости от экономической ситуации в предыдущем периоде =1, >1 или <1

Если , то =1; , >1 (предприниматели планируют увеличить предложение товаров и услуг); , <1

, где – чистые инвестиции на единицу прироста

, где – инвестиции со стороны спроса

, т.е. сбережения равны инвестициям

, разделим на s:

Из основного предположения определим Y(t):

, т.е. спрос равен предложению.

Но из основного предположения :

Темп прироста национального дохода:

Таким образом,

27. МОДЕЛЬ ЭК.РОСТА СОЛОУ Состояние экономики определяется с помощью 5 основных показателей:

Y(t) – национальный доход, C(t) – сбережения, I(t) – инвестиции, K(t) – капитал, L(t) – трудовые ресурсы

, где с – предельная норма сбережения

I(t)=v*Y(t), где v – чистые инвестиции на ед. прироста

Производственная дифференцируемая функция:

Прирост капитала и замена выбывших основных фондов:

– коэффициент выбытия

, где n – постоянный темп роста трудовых ресурсов

,

, т.к.

Капиталовооруженность:

Динамика капиталовооруженности:

Вывод формулы:

,

28. МОДЕЛЬ РАСШИР-СЯ ЭК-КИ НЕЙМАНА Имеется n технологических процессов, каждый из которых может выпускать 1 или несколько видов продукции. j – индекс технологических процессов, m – количество выпускаемых продуктов, i – индекс продукта

При единичной интенсивности j-й технологический процесс преобразует 1 набор продуктов в другой

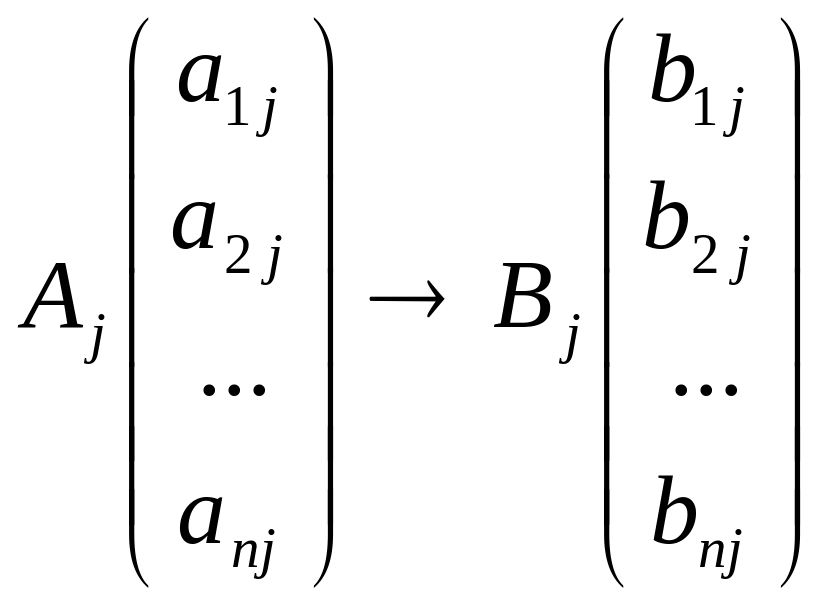, где – вектор затрат, – вектор выпуска.

Из векторов A_j и B_j можно составить матрицу затрат A и матрицу выпуска B:

– для каждого технологического процесса используется хотя бы 1 продукт

– каждый продукт производится хотя бы 1 технологическим процессом

– интенсивность j-го технологического процесса в году t

– выпуск i-го продукта j-м процессом в году t

– сколько i-го продукта было выпущено всеми технологическими процессами

– затраты i-го продукта для j-го технол. процесса в году t +1

– совокупные затраты i-го продукта

- соотношение между спросом (затратами) и предложением (выпуском)

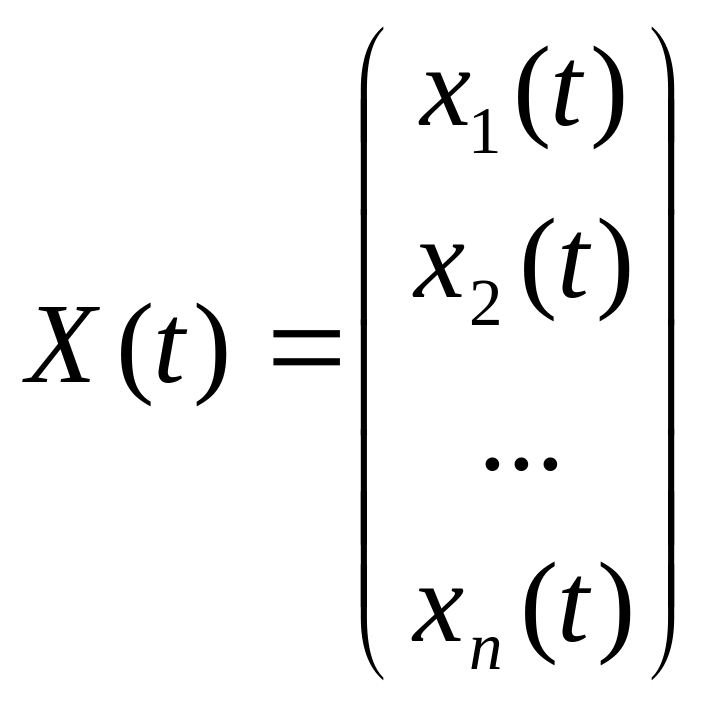– вектор интенсивности в году t

Система в матричном виде:

– связь между векторами интенсивности в годах t и t+1

– цена i-го продукта в году t,

Если для некоторого продукта существует строгое неравенство

, то для всех i

Т.к. существует равновесие и совершенная конкуренция, ни 1 технологический процесс не может получить прибыль

,

Если неравенство строгое, то (интенсивность j-го технологического процесса)

В экономике наблюдается сбалансированный рост, если интенсивности технологических процессов растут с одинаковым темпом (темп роста экономики)

Цены снижаются с одинаковым темпом :

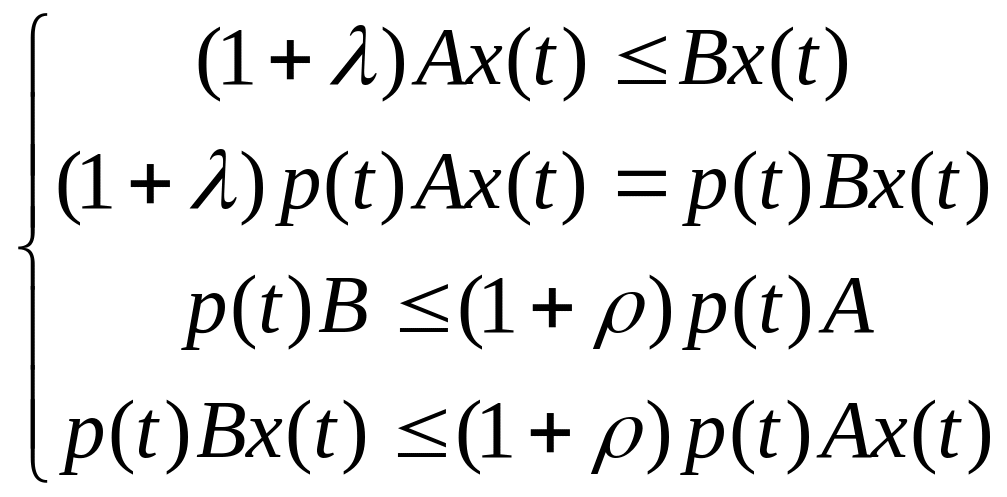
Система имеет решение, из него определяются интенсивности всех технологических процессов.

Сравнивая (2) и (4) из системы, получаем , т.е. темп роста экономики равен темпу роста цен: