Лекция 6 Законы распределения случайных величин
Ряд и многоугольник распределения дискретной случайной величины (СВ).
Условимся, что в дальнейшем Случайные величины будем обозначать большими буквами, а их соответствующие значения - малыми буквами.
Например Х – число попаданий при трех выстрелах; возможные значения: х1=0, х2=1, х3=2, х4=3.
Рассмотрим дискретную СВ Х с возможными значениями х1, х2,..,хn. В результате опыта СВ Х примет одно из этих значений, те произойдет одно из полной группы несовместных событий:
X=х1, Pi(i=1,2,…,n)
X=х2 P(X=x1)=P1, P(X=x2)=P2, P(X=xn)=Pn
Х=хn
Так как несовместные события образуют полную группу, то сумма i=1 до n равно Pi=1
Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим распределение вероятностей, те в точности укажем значение вероятности Pi и xi. Этим будет установлен закон распределения случайной величины Х.
Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающую связь между возможными значениями случайной величины и соответствующими им вероятностям.
Говорят, что случайная величина подчиняется данному закону распределения.
Простейшей формой задания закона распределения дискретной СВ является таблица:
xi |
x1 |
x2 |
… |
xi |
… |
xn |
Pi |
P1 |
P2 |
… |
Pi |
… |
Pn |
Такая таблица называется рядом распределения дискретной величины Х.
График построенный согласно этому ряду распределения называется многоугольником распределения.
x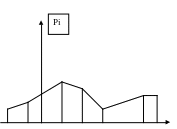
Многоугольник распределения, так же как и ряд распределения, полностью характеризует дискретную СВ и является одной из форм закона распределения.
Например Pi=F(xi)
Функция распределения.
Ряд распределения очевидно служит исчерпывающей характеристикой только для дискретной СВ. Для непрерывных СВ такую характеристику позволить нельзя, так как имеется несчетное множество значений случайной величины. Кроме того каждое отдельное значение непрерывной случайной величины обладает вероятностью равной нулю.
Для количественной характеристики распределений как дискретных так и непрерывных СВ используется вероятность события X<x, где х - некоторая текущая переменная.
Вероятность этого события очевидно зависит от Х и является некоторой функцией от Х. Эта функция называется функцией распределения величины Х и обозначается F(x).
# P(X<x)=F(x)
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин, как дискретных, так и непрерывных.
Функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствуют возможным значениям случайной величины.
При этом величина каждого скачка равна вероятности соответствующего значения дискретной СВ.
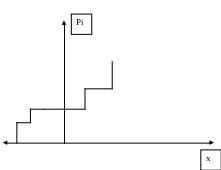
Сумма всех скачков равна 1.
По мере увеличения числа возможных значений СВ и уменьшения интервалов между ними число скачков становится больше, а сами скачки меньше.
Функция распределения непрерывной СВ обычно представляет собой функцию непрерывную во всех точках. Будем называть непрерывной СВ, СВ имеющую непрерывную функцию распределения.