
- •3. Теорема о разложении определителя. Теорема Лапласа.
- •4. Обратная матрица. Процедура ее нахождения. Аннулирование матриц.
- •5. Ранг матрицы. Способы нахождения.
- •6. Невырожденные системы слау. Способы решения.
- •7. Метод Гаусса. Произвольные слау. Теорема Кронекера-Капелли.
- •8. Однородные слау. Фундаментальная система решений.
- •10. Векторы на плоскости и в пространстве. Операции над векторами. Коллинеарность и компланарность. Базис. Координаты.
- •1. Умножение вектора на число:
- •2. Сумма двух векторов:
- •11. Скалярное произведение векторов. Определение. Вычисление. Свойства.
- •13. Смешанное произведение векторов. Определение. Вычисление. Свойства.
- •18. Взаимное расположение прямой и плоскости.
- •19. Эллипс.
- •20. Гипербола.
- •21. Парабола.
- •22. Эллипсоид.
- •22. Гиперболоид и конус.
- •24. Параболоид.
- •30. Графики в полярной системе координат и параметрически заданных функций.
- •27. Действительные числа.
- •32. Множества и операции над ними.
- •28. Предел последовательности.
- •29. Теоремы о пределах последовательности.
- •30. Предел функции.
- •31. Бесконечно малые и бесконечно большие функции.
- •32. Односторонние пределы.
- •33. Сравнение бесконечно малых.
- •34. Теоремы о пределах.
- •35. Первый замечательный предел.
- •36. Второй замечательный предел.
- •37. Непрерывность функции в точке. Классификация точек разрыва.
- •38. Теоремы о непрерывных функциях. Непрерывность на отрезке. Равномерная непрерывность.
- •39. Производная функции, ее геометрический и физический смысл.
- •40. Дифференциал. Дифференцируемость.
- •Свойства дифференциала.
- •41. Производная и дифференциал сложной функции.
- •42.Правила дифференцирования. Производные основных элементарных функций. Логарифмическое дифференцирование.
- •43. Производные и дифференциалы высших порядков. Производная параметрически заданных функций.
- •50.Асимтоты. Общая схема исследования функции
- •56. Предел, непрерывность и частные производные функции нескольких переменных.
- •57. Полный дифференциал. Производные высших порядков.
- •58. Касательная плоскость и нормаль к поверхности. Экстремум функции нескольких переменных.
- •59. Условный экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции нескольких переменных в области.
43. Производные и дифференциалы высших порядков. Производная параметрически заданных функций.
Производные и дифференциалы высших порядков.
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
![]()
Если найти производную функции f(x), получим вторую производную функции f(x).
![]()
т.е.
y
= (y)
или
![]() .
.
Этот процесс можно продолжить и далее, находя производные степени n.
![]() .
.
Производная функции, заданной параметрически.
Пусть
![]()
Предположим, что эти функции имеют производные и функция x = (t) имеет обратную функцию t = Ф(х).
Тогда функция у = (t) может быть рассмотрена как сложная функция y = [Ф(х)].
![]()
т.к.
Ф(х) – обратная функция, то

Окончательно
получаем:
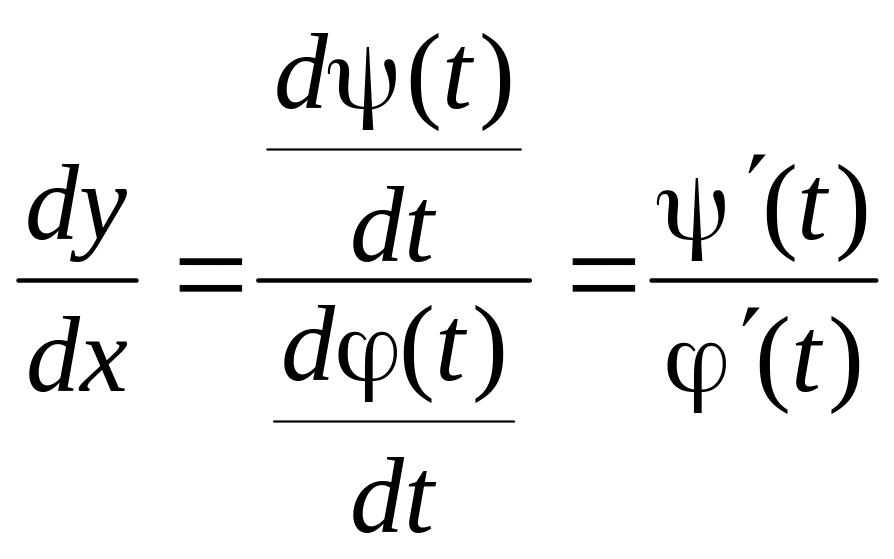
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
44-46. Теоремы о среднем. Правило Лопиталя-Бернулли. Формулы Тейлора и МакЛорена.
Теорема
Роля: Если
функция f(x)
непрерывна на отрезке [a,b],
дифференцируема на интервале (a,b)
и на концах отрезка принимает одинаковые
значения f(a)=f(b),
то найдется хотя бы одна точка
![]() ,
в которой производная
,
в которой производная
![]() обращается
в ноль, т.е.
обращается
в ноль, т.е.
![]() .
.
Теорема
Коши: Если
функции f(x)
и
![]() непрерывны на отрезке [a,b],
дифференцируемы на интервале (a,b),
причем
непрерывны на отрезке [a,b],
дифференцируемы на интервале (a,b),
причем
![]() для
для
![]() ,
то найдется хотя бы одна точка
,
такая, что выполняется равенство
,
то найдется хотя бы одна точка
,
такая, что выполняется равенство
![]() .
.
Теорема
Лагранжа:
Если функция
f(x)
непрерывна на отрезке [a,b],
дифференцируема на интервале (a,b),
то найдется хотя бы одна точка
такая, что выполняется равенство
![]() .
Это так же является формулой о конечном
приращении: приращение дифференцируемой
функции на отрезке [a,b]
равно приращению аргумента, умноженному
на значение производной функции в
некоторой точке этого отрезка. Если
производная функции равна нулю на
некотором промежутке, то функция
постоянна на этом промежутке. Если две
функции имеют равные производные на
некотором промежутке, то они отличаются
друг от друга на постоянное слагаемое.
Правило
Лопиталя (по раскрытию неопределенностей
вида 0/0) :
Пусть функции
f(x)
и
непрерывны и дифференцируемы в
окрестности точки
.
Это так же является формулой о конечном
приращении: приращение дифференцируемой
функции на отрезке [a,b]
равно приращению аргумента, умноженному
на значение производной функции в
некоторой точке этого отрезка. Если
производная функции равна нулю на
некотором промежутке, то функция
постоянна на этом промежутке. Если две
функции имеют равные производные на
некотором промежутке, то они отличаются
друг от друга на постоянное слагаемое.
Правило
Лопиталя (по раскрытию неопределенностей
вида 0/0) :
Пусть функции
f(x)
и
непрерывны и дифференцируемы в
окрестности точки
![]() и обращаются в ноль в этой точке: f(
)=
и обращаются в ноль в этой точке: f(
)=![]() .
Пусть
в окрестности точки
.
Если существует предел
.
Пусть
в окрестности точки
.
Если существует предел
![]() ,
то
,
то
![]() .
.
Правило
Лопиталя (по раскрытию неопределенностей
вида
![]() )
: Пусть
функции f(x)
и
непрерывны и дифференцируемы в
окрестности точки
(кроме, может быть, точки
),
в этой окрестности
)
: Пусть
функции f(x)
и
непрерывны и дифференцируемы в
окрестности точки
(кроме, может быть, точки
),
в этой окрестности
![]() .
Если существует предел
.
Если существует предел
![]() .
.
47-48.Монотонность функции. Экстремум. Необходимые и достаточные условия.
Теорема(необходимые
условия).
Если дифференцируемая на интервале
(a,b)
функция f(x)
возрастает (убывает), то
![]() для любых
для любых
![]() .
Док-во. Пусть
функция f(x)
возрастает на интервале (a,b).
Возьмем произвольные точки х и х +
.
Док-во. Пусть
функция f(x)
возрастает на интервале (a,b).
Возьмем произвольные точки х и х +
![]() на интервале (a,b)
и рассмотрим отношение
на интервале (a,b)
и рассмотрим отношение
![]() .
Функция f(x)
возрастает, поэтому если
>0,
то x+
>x
и f(x+
)>f(x);
если
<0,
то x+
>x
и f(x+
)<f(x).
В обоих случаях
>0,
так как числитель и знаменатель дроби
имеют одинаковые знаки. По условию
теоремы функция f(x)
имеет производную в точке x
и является пределом рассматриваемого
отношения. Следовательно,
.
Функция f(x)
возрастает, поэтому если
>0,
то x+
>x
и f(x+
)>f(x);
если
<0,
то x+
>x
и f(x+
)<f(x).
В обоих случаях
>0,
так как числитель и знаменатель дроби
имеют одинаковые знаки. По условию
теоремы функция f(x)
имеет производную в точке x
и является пределом рассматриваемого
отношения. Следовательно,
![]() .
Аналогично рассматриваем тот случай,
когда функция f(x)
убывает на интервале (a,b).
Данная теорема означает, что касательные
к графику возрастающей дифференцируемой
функции образуют острые углы с
положительным направлением оси Ox
или в некоторых точках параллельны оси
Ox.
.
Аналогично рассматриваем тот случай,
когда функция f(x)
убывает на интервале (a,b).
Данная теорема означает, что касательные
к графику возрастающей дифференцируемой
функции образуют острые углы с
положительным направлением оси Ox
или в некоторых точках параллельны оси
Ox.
Теорема(достаточные
условия).
Если функция f(x)
дифференцируема на интервале (a,b)
и
![]() для
для
![]() ,
то эта функция возрастает (убывает) на
интервале (a,b).
Док-во. Пусть
,
то эта функция возрастает (убывает) на
интервале (a,b).
Док-во. Пусть
![]() .
Возьмем точки
.
Возьмем точки
![]() и
и
![]() из интервала (a,b),
причем
>
.
Применим к отрезку [
,
]
теорему Лагранжа: f(
)
- f(
)=
из интервала (a,b),
причем
>
.
Применим к отрезку [
,
]
теорему Лагранжа: f(
)
- f(
)=![]() ,
где
,
где
![]() .
По условию
.
По условию
![]() .
Следовательно, f(
)
- f(
)>0
или f(
)>f(
),
т.е. функция f(x)
на интервале (a,b)
возрастает. Возрастающая или убывающая
функция называется монотонной. Теорема
(необходимое условие экстремума).
Если дифференцируемая функция y=f(x)
имеет экстремум в точке
,
то ее производная в этой точке равна
нулю:
.
Следовательно, f(
)
- f(
)>0
или f(
)>f(
),
т.е. функция f(x)
на интервале (a,b)
возрастает. Возрастающая или убывающая
функция называется монотонной. Теорема
(необходимое условие экстремума).
Если дифференцируемая функция y=f(x)
имеет экстремум в точке
,
то ее производная в этой точке равна
нулю:
![]() .
Док-во:
Пусть, для определенности,
-точка
максимума. Значит, в окрестности точки
выполняется неравенство
.
Док-во:
Пусть, для определенности,
-точка
максимума. Значит, в окрестности точки
выполняется неравенство
![]() .
Но тогда
.
Но тогда
![]() ,
если
>0,
и
,
если
>0,
и
![]() ,
если
<0.
По условию теоремы производная
,
если
<0.
По условию теоремы производная
![]() существует. Переходя к пределу, при
существует. Переходя к пределу, при
![]() ,
получим
,
получим
![]() ,
если
<0
и
,
если
<0
и
![]() ,
если
>0.
Поэтому :
.
Теорема
(достаточное условие экстремума): Если
непрерывная функция f(x)
дифференцируема в некоторой
,
если
>0.
Поэтому :
.
Теорема
(достаточное условие экстремума): Если
непрерывная функция f(x)
дифференцируема в некоторой
![]() -окрестности
и критической точки
и при переходе через нее 9слева направо)
производная
меняет
знак с плюса на минус, то
есть точка максимума; с минуса на плюс,
то
-точка
минимума. Док-во:
рассмотрим
-окрестность
точки
.
Пусть выполняются условия:
-окрестности
и критической точки
и при переходе через нее 9слева направо)
производная
меняет
знак с плюса на минус, то
есть точка максимума; с минуса на плюс,
то
-точка
минимума. Док-во:
рассмотрим
-окрестность
точки
.
Пусть выполняются условия:
![]() и
и
![]() .
Тогда функция f(x)
возрастает на интервале
.
Тогда функция f(x)
возрастает на интервале
![]() ,
а на интервале
,
а на интервале
![]() она убывает. Отсюда следует, что значение
f(x)
в точке
является наибольшим на интервале
она убывает. Отсюда следует, что значение
f(x)
в точке
является наибольшим на интервале
![]() ,
т.е. f(x)<f(
)
для всех
,
т.е. f(x)<f(
)
для всех
![]() .
Это и означает, что
- точка максимума функции.
.
Это и означает, что
- точка максимума функции.
49. Выпуклость, вогнутость, точки перегиба. Необходимые и достаточные условия. Асимптоты. Общая схема исследования функции.
- График функции y=f(x) назыв. выпуклым (вверх) на отрезке [a,b], если он расположен ниже касательной. Для дифференцируемой на [a,b] функции график расположен ниже любой касательной; для недифференцируемой функции график расположен выше хорды((a, f(a) и (b, f(b))).
- График функции назыв. вогнутым (выпуклым вниз) на [a,b], если он расположен выше касательной (ниже хорды). Если в левой U( ) график функции выпуклый в одну сторону, а в правой окрестности в другую сторону, то -точка перегиба.
-
Если функция y=f(x)
дважды дифференцируема на [a,b]
и для любых
![]() ,
то график является выпуклым
вниз(вогнутым).
Если
,
то график является выпуклым
вниз(вогнутым).
Если
![]() ,
то график является выпуклым. Достаточное
условие точки перегиба:
Пусть f
- дважды дифференцируемая функция в
окрестности
и
,
то график является выпуклым. Достаточное
условие точки перегиба:
Пусть f
- дважды дифференцируемая функция в
окрестности
и
![]() или
или
![]() не
существует. Если при этом для любых
не
существует. Если при этом для любых
![]() ,
а для любых
,
а для любых
![]() ,
то
- точка перегиба.
,
то
- точка перегиба.
