10. Векторы на плоскости и в пространстве. Операции над векторами. Коллинеарность и компланарность. Базис. Координаты.
Вектор – направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец.
1. перенос отрезка при помощи параллельного переноса, не изменяет вектор.
2. вектор задается «длиной вектора» и направления.
3. если у вектора изменить направление на противоположное, то получаем противоположный вектор.
4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно).
Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.
Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.
Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.
Примечание: два вектора в пространстве всегда компланарны.
Примечание: два вектора называются равными, если они сонаправлены и равны по длине.
Линейные операции над векторами:
1. Умножение вектора на число:
Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля.
2. Сумма двух векторов:
Есть вектор, получаемый из слагаемых при помощи правила параллелограмма или правила треугольника.
Базис пространства -совокупность длин независ векторов, по которым можно разложить любой вектор этого пр-ва.
Базис 3x мерного пр-ва образует любая тройка некомпланарных векторов пр-ва.
Если
образуют
базис в пространстве, то любой вектор
из
этого пространства может быть представлен:
Примечание:
для конкретно-заданного базиса не
всегда просто бывает найти коэффициент
.
Проще всего это сделать когда базис является ортонормированным.
Понятие ортонормированности распадается на понятия ортогональности и нормированности.
( перпендикулярность и длина=1).
В
3-х мерном пространстве
ортогональный
базис состоит из 3 взаимноперпендикулярных
векторов.
Ортонормированный базис состоит из 3-х взаимноперпендикулярных векторов, длина каждого из которых = 1.
11. Скалярное произведение векторов. Определение. Вычисление. Свойства.
Скалярное произведение векторов - число = произвед длин на косинус между ними.
Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось.
Свойства:
1. a*b=b*a
2. (C*a)*b=C*(a*b)
3. a(b+c)=a*c+b*c;
4.
5. (a, b) =
0 =>
6. ij = jk = kj = 0.
Теорема 1: в
пространстве R3
в ортонормированном базисе
:
Следствие
из Т1:
Для
вектора
:
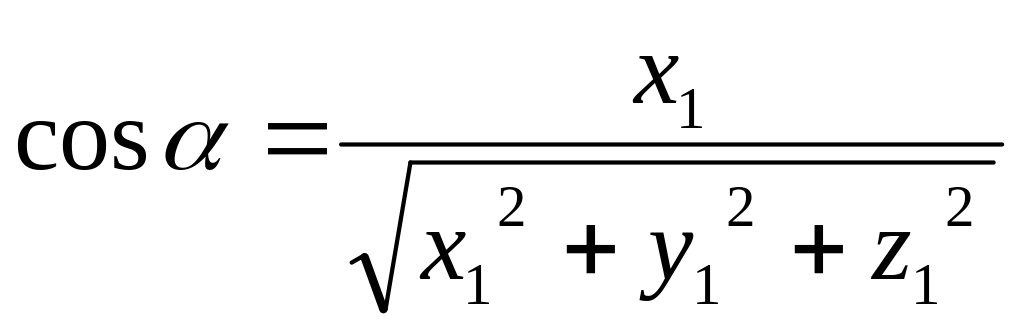
Механический смысл скалярного произведения:
Пусть
-
сила, которая перемещает тело в
направлении вектора S
( на длину
)
=>
12. векторное произведение векторов. Определение. Вычисление. Свойства.
Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой.
Векторное произведение вектора a на b - это c, который:
1)с перпендикулярно a и b;
2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку.
Замечание: Из определения вытекает след соотношения между ортами ijk:
1. i*j=k;
2. j*k=i;
3. k*i=j;
Свойства:
1)векторное
произ при перестановке множителей
меняет знак. (
)
2)два ненулевых вектора коллинеарны, когда их векторное произв =0.
Пункты: 1)условие коллиниарности: a//b => a*b=0;
2)нахождение
S
параллелограмма и S
треуг. Sпар=
sin
.
Sтр=0,5*
3)определение момента силы. |M|=|F|*|S|.
Теорема:
,
