1)Кручение- такой вид деф, когда в попер сечении эл-та констр возник 1-а внутренняя сила – крутящий момент (Мк).

Кручению подверг многие детали машин и механизмов. Кручение прямого бруса происходит при нагружении его внешними закручивающ моментами (т), действ-щими ┴ к продольной оси бруса.

Моменты, вызывающие деформацию кручения, называются крутящим моментом . величина крутящего момента, действующего в каком – либо сечении вала определяется методом сечений.

Внутренние силы при кручении

Если брус нах в сост покоя или равном движ, то алгебр сумма всех внешних моментов = 0.

Внутр силы опред методом сечения: мысленно вал рассечём за т₂ и одну часть (правую) отбросим:

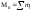
Крутящий момент в сечении числ =, алгебр сумме моментов наход по одну стор от сечения.

Дифференциальная зависимость между крутящим моментом и распределённой скручивающей нагрузкой(dM_k/dz=+-m).

2) Условие прочности при кручении

ρ = ρ_тах = r

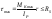
Обозначим

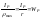-полярныймом.Сопрот

;

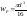
R_S – расчётное сопрот на срез или сдвиг

W_P – полярный мом сопрот наз отнош полярн мом инерции к расстоянию от ц.т. сечения до наиб удалён точки.

Условие жёсткости при кручении

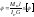
Угол закручивания на уч-ке вала не должен превышать допуск знач [φ] = 0,3-3⁰

3) Напряжение при кручении

Номальное напряж в попер сечении при круч = 0.

Касат напряж опр по ф-ле:

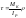
М_к – крут мом, где располож исслед точка

ρ – расст от цт до точки

I_P – полярный момент инерции

Д-мма 1-го сечения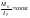

Из ф-лы видно:

ρ = 0, τ = 0

ρ = ρ_тах, τ = τ_тах

-Гипотезы при кручении : 1) поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);

2) расстояния между поперечными сечениями не изменяются, следовательно ;

3) контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Ог..

4) материал стержня подчиняется закону Гука

Жёсткости при кручении

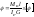
4)Напряжение при кручении

Номальное напряж в попер сечении при круч = 0.

Касат напряж опр по ф-ле:

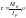
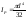
М_к – крут мом, где располож исслед точка

ρ – расст от цт до точки

I_P – полярный момент инерции

Д-мма 1-го сечения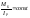

Из ф-лы видно:

ρ = 0, τ = 0

ρ = ρ_тах, τ = τ_тах

5) Угол закручивания при кручении

Угол приходящийся у на единице длины, наз относит углом закруч:

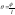
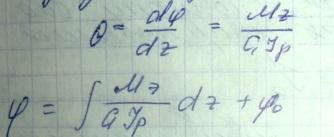
Где угол поворота при Z=0. В случае если Mz=const=M, жесткость сечения GJр=const =0

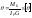
- задается технич условиемиз двух диаметров вала при расчете на прочность и жесткость выбирается больший

6)Статически неопределимыми называются такие системы, опорные реакции в которых и (или) внутренние усилия невозможно определить только уравнений равновесия.

По сравнению с системами статически определимыми указанные системы имеют дополнительные связи, которые называют лишними связями. Усилия, возникающие в лишних связях, называют лишними неизвестными.Термин «лишние» следует понимать как «избыточные», а не как «ненужные». Наличие лишних связей делает систему более жёсткой и более экономичной.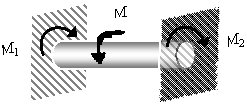

Рис:статич. Неопред.система при кручении

Для расчета статически неопределимых систем применяют несколько методов, из которых в сопротивлении материалов рассматривают метод сил.

В опорах возникнут опорные моменты 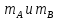. Составим ур-ние равновесия: 1. 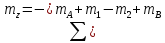=0 В этом ур-нии два неизвестных момента 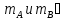сис-ма 1 раз статически неопределима. Поэтому необходимо составить дополнительное ур-ние, рассмотрев деформацию сис-мы.

7) В отличии от круглых брусьев, при кручении которых сечение остаёься плоским, сечения стержней любой другой формы искривляются. При этом различные точки одного поперечного сечения смещаются друг относительно друга, параллельно оси стержня – происходит так называемая депланация поперечного сечения.

Принцип сен – виана - в теории упругости — положение, согласно которому уравновешенная система сил, приложенная к некоторой части твёрдого тела, вызывает в нём появление неравномерности распределения напряжений, которая быстро уменьшается по мере удаления от этой части. На расстояниях, больших максимального линейного размера зоны приложения нагрузок, неравномерность распределения напряжения и деформации оказываются пренебрежительно малыми. Свободное кручение - кручение, при котором депланация во всех сечениях одинакова. При этом в поперечном сечении возникают только касательные напряжения. Стесненное кручение - кручение, при котором наряду с касательными напряжениями в поперечных сечениях стержня возникают также нормальные напряжения. Стесненное кручение связано с тем, что депланация в различных сечениях стержня различна..

Mk=G*Jk – жёсткость при свободном кручении.

8)

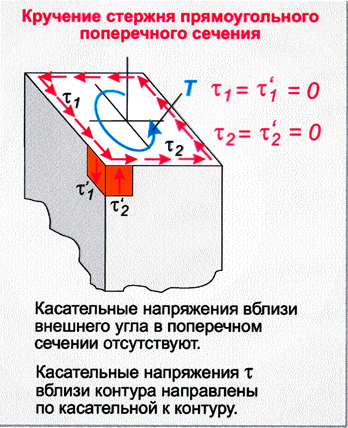
При кручении стрержня прямоугольного сечения гипотеза плоских сечений не выполняется, сечения искривляются или деформируются. В поперечных сечениях возникают касательные напряжения, кот. возможно определить только методами теории упругости. Эпюра распределения 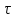в поперечном сечении имеет вид. 2 касательное напряжение максимально и определяется по ф-л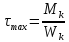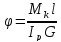е:; где 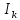– приведенный момент инерции; - приведенный момент сопротивления.

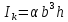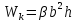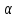; где и - коэффициенты, зависящие от соотношения длин сторон прямоугольника

9) Брус считается тонкостенным, если толщина существенно меньше его прочих линейных размеров. Линия делящая толщину сечения пополам, называется средней линией или контуром сечения. Средняя линия может быть замкнутой или незамкнутой

10) В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции. Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях. Внутренние усилия определяют методом сечений, который состоит в следующем. Если тело находится в равновесии, то его левая и правая части относительно воображаемой поверхности раздела тоже находятся в равновесии. Внутренние усилия Nx, Ny и S действуют в срединной плоскости пластины и называются нормальными и сдвигающей силами. При поперечном изгибе пластины эти внутренние усилия равны нулю.

Диференц.зависимость:

11)

Как показал опыт эксплуатации изгибаемых элементов конструкций, разрушение их начинается с крайних волокон, где возникают наибольшие норм. напряжения

12) Как показал опыт эксплуатации изгибаемых элементов конструкций, разрушение их начинается с крайних волокон, где возникают наибольшие норм. напряжения

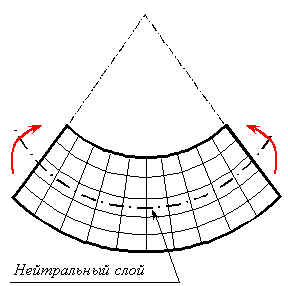При плоском изгибе, нейтральные слои образуют цилиндрическую поверхность,образующие которой лежат в поперечных сечениях и называются нейтральными линиями. Нейтральный линии так же как и нейтральные слои служат границами между растягивающим и сжимающими напряжениями. На самой нейтральной линии напряжений нет.

13) При поперечном изгибе в сечении балки помимо изгибающего момента возникает поперечная силаПоэтому в поперечном сечении при поперечном изгибе наряду с нормальными напряжениями () возникают и касательные напряжения ().формула нормальных напряжений при поперечном изгибе: .

формулу Журавского: где Q — поперечная сила; S^*_x — статический момент отсечённой части поперечного сечения относительно оси х, F^* — площадь отсечённой части поперечного сечения, y_c — расстояние от центра отсечённой части поперечного сечения до оси х, J_x — главный осевой момент инерции полного сечения, b_y — ширина сечения в той точке, для которой находится напряжение

14) касательное и нормальное напряжение действующие на главной площадке называется главным(экстремальным) главные напряжения, выражая из через s и t: .

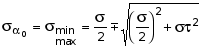15) Расчеты на прочность при прямом поперечном изгибе производятся по нормальным напряжениям. С этой целью исследуются эпюры изгибающих моментов и находится наиболее опасное сечение При сечениях простой геометрической формы, согласно соотно­шениям, формулы для вычисления W_z  при­нимают вид:

- для круга                

-для кольца     - для прямоугольника        

       Особенно сильно изгибу подвер­гаются детали, у которых поперечные размеры значительно меньше продольных.  

16) 

17)

Рассмотрим балку нагруженную силой F.

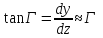
– первая производная от прогиба равна углу поворота сечения

Ранее была установлена зависимость 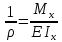; из высшей математики известно 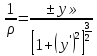, т.к. 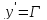– величина малая, ей можно пренебречь, получим

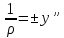
Приравниваем правые части ур-ий

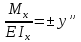
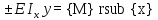- приближённое дифференциальное ур-е изогнутой оси балки.

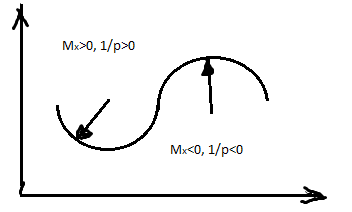
Знаки кривизны и изгибающего момента совпадают если изогнутую ось поместить в 1-ом квадранте координатных осей т.е. начало координат выбирать в центре тяжести крайнего левого сечения балки, ось ординат направлять вверх, ось абсцисс совмещать с осью прямой балки : M_x>0, 1/p>0; M_x<0, 1/p<0.

18) Для определения Ɵ и y проинтегрируем диф-ое уравнене

; ; ;

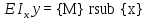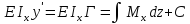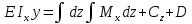C и D – постоянные интегрирования, определ. из граничных условий закрепления балки.

Для консольной балки найти y_max и Ɵ_max

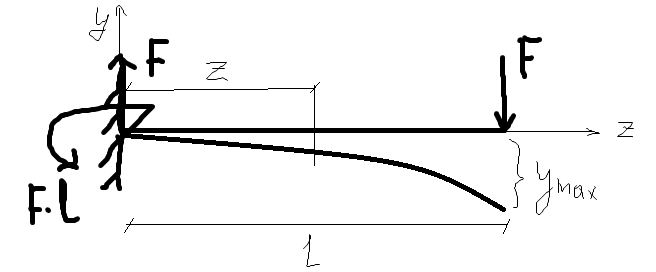
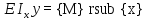
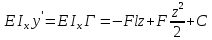
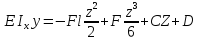
Определим постоянные интегрирования C и D

При Z=0 (защимление) : y₀=0, Ɵ₀=0

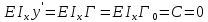
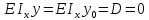
найдём y_max и Ɵ_max при z=l

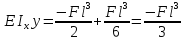
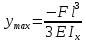
Знак «-» угла поворота указывает что сечение повернулось по часовой стрелке, а знак «-» у прогиба означает что прогиб произошёл вниз.

19)

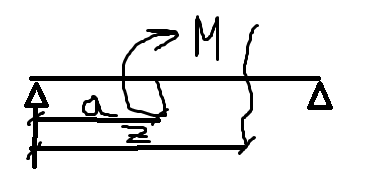
Рассм. Загруженную балку (рисунок!):

Под действием нагрузок балка деформируется и в начале координат прогиб будет

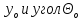
Запишем приближенное диф-ное ур-е для ряда участков.При записи ур-й использ. Правило знаков как для изгибающего момента.

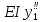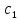1 уч. =0; EI=; EIy=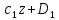

2 уч. EI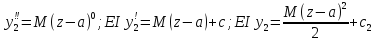z +

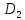
3 уч. EI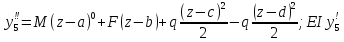=M(z-a)+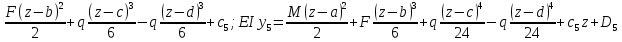

На смежных участках углы поворота и прогибы одинаковы. При z=a; =;

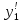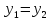
Из выражений углов поворота и прогибов следует: 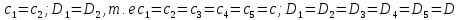. Для выяснения физической сущности постоянных интегрирования С и D рассм. 1 уч.: При z=0;

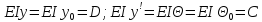
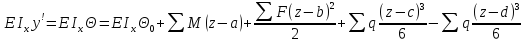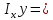Вывод: Постоянные интегрирования С и D представляют собой угол поворота и прогиб в начале координат,умноженные на жесткость балки. Можно записать обобщенное ур-е изогнутой оси балки. ; E E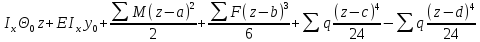

В этих ур-х нач. параметры E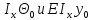 неизвестны. Их необходимо определить. Поэтому этот метод получил название-метод начальных параметров.

20) Работа силы первого состояния на перемещении, вызванном силой второго состояния, равняется работе силы второго состояния на перемещении, вызванном силой первого состояния:

Первый индекс в обозначении перемещений показывает точку и направление перемещения, второй – причину перемещения.

21) Методы определения перемещений основаны на принятом рав-ве работы внешних сил на перемещениях в упругой системе и потенциальной энергии упругой деформации системы. W=U. Эти методы явл. Универсальными и нашли широкое применение. Работа статически приложенной внешней силы = ½ произведения конечного значения силы на конечное значение соответствующего перемещения.

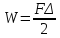– теорема Клайперона

Работа произвольной сис-мы сил равна:

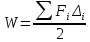
При применении энергетич. Метода как линейные, так и угловые перемещения обозначают Δ.

Для определения работы внутренней силы, численно равной потенциальной энергии деформации, выделим из балки, находящейся в условиях чистого изгиба бесконечно малый элемент dz.

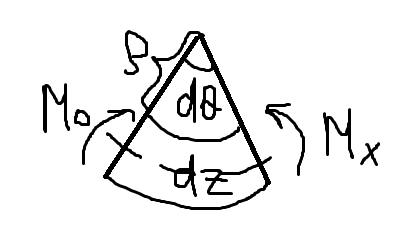Из курса теор. Механики известно,что работа момента=его произведению на соотв. угол поворота. Учитывая статический характер нагрузки,получим: dW=dU=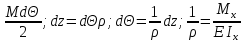; dΘ=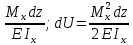

Это выражение даёт величину потенциальной энергии для элемента балки, находящегося в условиях чистого изгиба. При поперечном изгибе, когда кроме изгибающего момента, возникают и поперечные силы,ф-ла для вычисления энергии будет иметь вид: dU=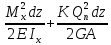

Коэффициент К зависит от размеров сечения и в какой-то мере учитывает неравномерность распределения касат.напр-й по сечению. При вычислении энергии деф-ции изгиба поперечными силами Q можно пренебречь, т.к. последнее слагаемое составляет 2-3% от всей энергии деф-ции.

Для вычисления энергии деф-ции балки в целом следует просуммировать значение dU по всей её длине. Окончательная ф-ла для определения энергии деф-ции при изгибе имеет вид:

22) Формулы Мора для определения перемещений

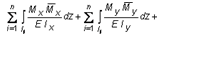
где F - площадь всего сечения двутавра, F_CT - площадь стенки; Nz , Qx , Qy , Mz , Mx , My - внутренние силовые факторы, возникающие в поперечных сечениях заданной стержневой системы;

-внутренние силовые факторы, возникающие в поперечных сечениях заданной системы, от действия усилия Ф = 1.

Подробно рассмотрим случай, когда брус работает только на изгиб (Mx ¹ 0, Nz = Mz = My = Qx = Qy = 0). В этой ситуации выражение принимает вид:

23) Правило Верещагина для определения перемещений

Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.