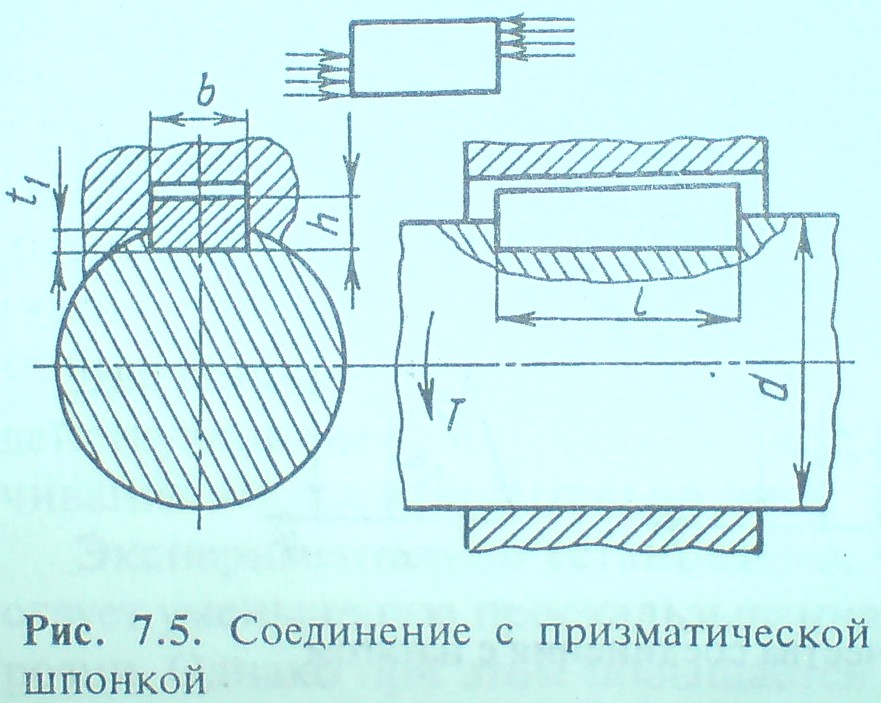
36. Шпоночные соединения, виды шпонок, назначение, проверочный расчет призматической шпонки на прочность, допускаемые напряжения.

_{Шпоночными} называют разъёмные соединения составных частей изделия с применением шпонок, предназначенные в основном для передачи вращательного движения, применяются при отсутствии особых требований к точности центрирования соединяемых деталей. Шпоночные соединения могут быть неподвижными и подвижными и служат обычно для предотвращения относительного поворота ступицы и вала при передаче вращающего момента. Шпоночные соединения широко применяют во всех отраслях машиностроения. По форме шпонки разделяются на призматические, клиновые, сегментные и тангенциальные. Призматические и сегментные шпонки создают ненапряжённые соединения ступицы с валом, клиновые и тангенциальные-напряжённые соединения, в кот. поверхности шпонки и сопряжённых с ней деталей находятся в напряжённом состоянии ещё до передачи нагрузки. 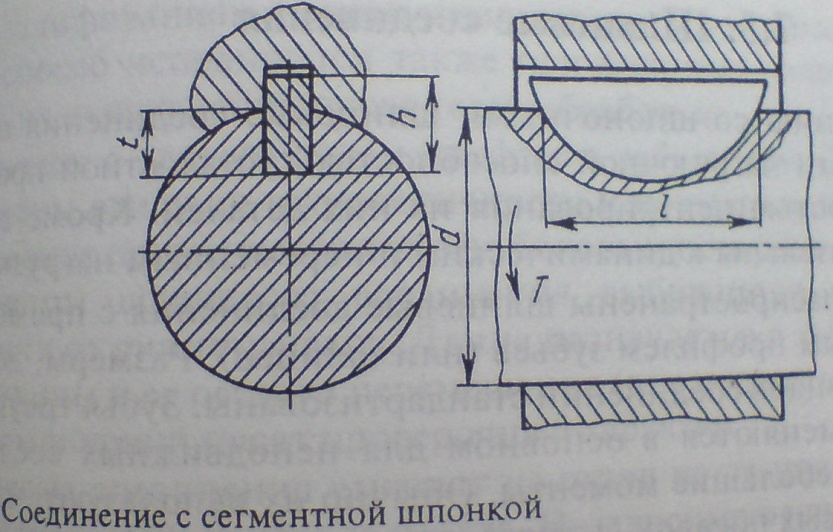Высокие призматические шпонки применяются для ступиц из чугуна и других материалов более низкой прочности, чем материал вала.Соединения сегментными шпонками применяются при валах небольших размеров и сравнительно коротких ступицах колёс. Проверочный расчёт: напряжение смятия узких граней не должно превышать допускаемого, т.е. рассчитывается по формуле: , где Т-передаваем вращающий момент,d-диаметр вала в месте установки шпонки, l_p-рабочая длина шпонки. При стальной ступице и спокойной нагрузке допускаемое напряжение смятия

3 7. Особенности геометрии, кинематики и расчета на прочность цилиндрических косозубых передач.

У косозубых колес зубья расположены на винтовых линиях, на разделительном цилиндре. Шаг волновых линий по делительному цилиндру много меньше ширины колеса, поэтому криволинейность зуба малозаметна и зуб внешне прямолинеен, но наклонен к оси зубчатого колеса на некоторый угол. Образование боковой эвольвенты поверхности зуба можно представить, если перекатывать без скольжения плоскость ТТ’ по основному цилиндру диаметром d_в и осью ОО. некоторая прямая ВВ в плоскости ТТ составляет угол β с образующей цилиндра АА, параллельной его оси ОО. При перекатывании плоскости ТТ каждая из точек прямой ВВ опишет в пространстве эвольвенту, а сама прямая – винтовую поверхность. В каждом поперечном сечении этой поверхности эвольвенты имеют начальные точки, расположенные по винтовой линиина цилиндре. При нарезании косозубого колеса по методу обкатки, инструмент в виде рейки со стандартным контуром устанавливают под углом β к оси вращения заготовки.

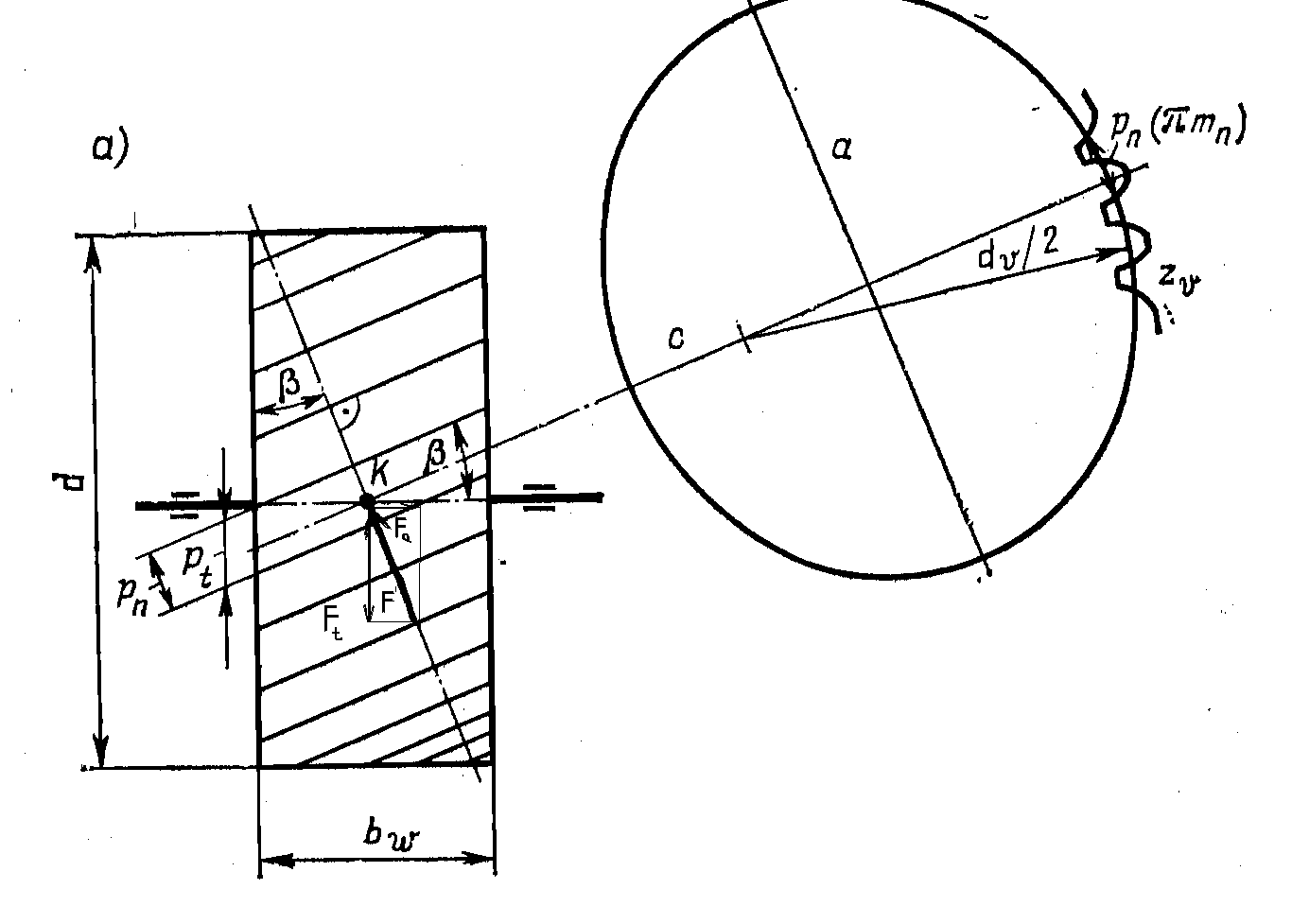Особенность расчёта: так как профиль зуба определяется двумя модулями(торцевым и нормальным), то проведя сечение по нормали к профилю зуба получим эллиптическое сечение а зуб получается прямой.С учетом наклона зуба геометрические размеры колес рассматриваются в двух сечениях: торцевом tt, перпендикулярном оси вращения ОО, и нормальном nn, перпендикулярном боковой поверхности зуба. Соответственно различают 2 шага: торцевой P_t и нормальный P_n : , и 2 модуля: m_t и m_n : ,

где β – угол наклона зубьев на делительном цилиндре.

За стандарт принимают m_n = m, который должен соответствовать ГОСТу и являться исходной величиной для геометрических расчетов колес и зацепления. Диаметр делительной окружности:

Остальные геометрические размеры находят по справочным формулам.

Зубчатую передачу можно образовывать только из косозубых колес с одинаковым модулем, у которых углы наклона зубьев равны по величине, но противоположны по знаку.

Передаточное отношение косозубых колес определяется в виде:

Межосевое расстояние:

Из формулы видно, что косозубые передачи позволяют изменить межосевое расстояние за счет изменения угла наклона β. По сравнению с прямозубыми они обеспечивают большую плотность зацепления, работают относительно бесшумно, с малыми динамическими нагрузками при высоких скоростях, так как зубья соприкасаются не сразу по всей ширине, а постепенно. Это обеспечивает большую величину коэффициента перекрытия, в зацеплении может одновременно находиться и одна и несколько пар зубьев (β = 8…15 град, ε = 2).

В косозубой передаче расчетная нагрузка F действует по линии зацепления NN, и ее можно разделить на составляющие по трем взаимно перпендикулярным направлениям; окружное усилие действует по касательным к делительным окружностям колес; радиальное усилие

, , - осевое усилие.

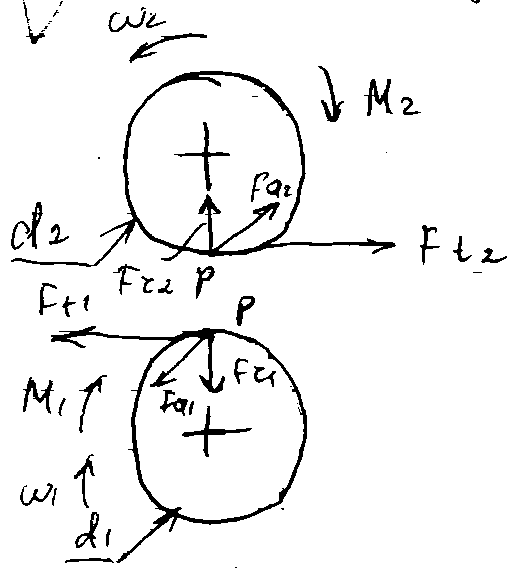О севое усилие действует по оси вращения колеса и стремится сдвинуть колесо по оси вала. Это является недостатком косозубых механизмов и требует установки в опорных узлах радиально-упорных подшипников. Распределение сил на ведущем и ведомом колесах – смотри рисунок b.

Из геометрии косозубого колеса следует, что профиль косого зуба в нормальном сечении NN соответствует профилю прямого зуба некоторого прямозубого колеса. Это дает основание рассчитывать косозубые колеса на прочность по формулам, полученным для прямозубых колес, но с учетом их геометрии. В нормальном сечении NN косозубого колеса получается делительный эллипс с полуосям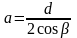и и . Радиус кривизны эллипса в полюсе Р:

При расчете косозубых колес на прочность, их приводят к эквивалентным прямозубым, исходя из условия: косозубое колесо с некоторым числом зубьев z считается равнопрочным эквивалентному прямозубому колесу с числом зубьев z_экв , если радиус кривизны делительного эллипса косозубого колеса в точке Р равен делительной окружности эквивалентного прямозубого колеса.

Для эквивалентного прямозубого цилиндрического колеса , для косозубого колеса: .

Принимая модуль косозубого колеса в нормальном сечении m_n равным модулю эквивалентного прямозубого колеса, получим:

где - коэффициент формы зуба, соответствующий приведенному числу зубьев z_э.

K_M = 1,2 – коэффициент увеличения нагрузки на косозубое колесо, учитывающий большую поверхность соприкосновения зубьев косозубого колеса по сравнению с прямозубым.

     Эквивалентное зубчатое колесо – эвольвентное прямозубое цилиндрическое зубчатое колесо, размеры и форма зубьев которого в торцовом сечении приближенно совпадают с размерами и формой зуба эвольвентного косозубого цилиндрического зубчатого колеса в сечении его зуба плоскостью, нормальной к линии, равноудаленной от разноименных теоретических линий зуба и лежащей на одной с ними соосной цилиндрической поверхности.