17) Прямая на плоскости: каноническое уравнение, параметрическое уравнение, нормальное уравнение.

 Нормальное уравнение прямой  где   - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Параметрические уравнения прямой

Параметрические уравнения прямой могут быть записаны в виде:

где t — производный параметр, a_x, a_y — координаты x и y направляющего вектора прямой, при этом

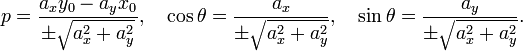
Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении. Каноническое уравнение прямой

Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:

где   — координаты   и   направляющего вектора прямой,   и   координаты точки, принадлежащей прямой.

18) Плоскость в пространстве: общее уравнение, уравнение в отрезках, нормальное уравнение.

Общее уравнение относительно переменных x, y, z называется уравнение вида Ax + By + Cz + D = 0, где хотя бы один из коэффициентов А, В, С отличен от нуля.

Уравнение плоскости в отрезках

, где  ,   и   - отрезки, отсекаемые плоскостью на осях  ,   и   соответственно.

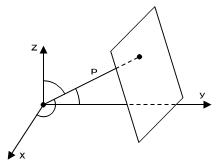
Нормальное уравнение плоскости (в координатной форме)

, где   - длина перпендикуляра, опущенного из начала координат на плоскость, а углы  ,   и   - углы, образованные этим перпендикуляром с осями  ,   и   соответственно.

19) Прямая в пространстве: общие уравнения, каноническое и параметрическое уравнения.

Рассмотрим прямую на плоскости. Общим уравнением прямой на плоскости называют уравнение  . Если прямая задана в ортонормированном базисе и вектор   имеет единичную длину, эта формула называется нормальным уравнением прямой.

Параметрическим уравнением прямой называют задание прямой в виде      Вектор (α,β) называют направляющим, а точку   - начальной.

Каноническим уравнением прямой называют уравнение 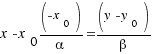   Термины направляющий вектор и начальная точка вводятся для канонического уравнения так же, как и для параметрического уравнения (и имеют тот же смысл).

Каноническое уравнение прямой в пространстве Каноническое уравнение прямой в пространстве имеет вид:  Где,  ,  ,   - координаты точки, лежаей на плоскости, а m, n и p - координаты направляющего вектора прямой.

Параметрическое уравнение прямой в пространстве Параметрическое уравнение прямой в пространстве имеет следующий вид: 

20) Эллипс.

Определение. Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

Внешний вид уравнения какого-либо геометрического места точек зависит от взаимного расположения этого множества точек и декартовой системы координат.

Выберем прямоугольную систему декартовых координат так, чтобы ось абсцисс проходила через оба фокуса F₁ и F₂, начало координат находится в середине отрезка F₁F₂ (рис. 7). Если обозначить расстояние между фокусами F₁ и F₂ через 2с, тогда координаты фокусов будут соответственно (-с, 0) и (с, 0).

Пусть М(х, у) - текущая точка эллипса (рис. 7).

Обозначим сумму расстояний F1M и F2M через 2а (a > c по правилу треугольника), т.е.  , или

Уравнение (36) и есть уравнение эллипса. Приведем его к более простой для исследований форме:

Поскольку a > c, то можно обозначить

тогда получаем Окончательно получим (при выбранной системе координат) уравнение

Уравнение (38) называют каноническим уравнением эллипса.

Замечание. Т.к. в процессе преобразований дважды возводились в квадрат обе части уравнения, то необходимо проверить, не получены ли "лишние" точки. Для этого нужно показать, что если координаты произвольной точки M₀(x₀, y₀) удовлетворяют уравнению (38), то 

Эта задача предлагается студентам для самостоятельного решения.

Сделаем некоторые замечания о форме эллипса. Из уравнения (38) понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.

Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать уравнение (38) в виде:

Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0 (рис. 8).

Числа а и b называют полуосями эллипса.

Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс (рис. 9).

Если изменяется величина с, то меняется форма эллипса, а именно: если   и при c = 0 эллипс становится окружностью с уравнением  Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой. Если же   , то  , т.е. эллипс сжимается вдоль оси Оу. Величина   может служить числовой характеристикой сжатия эллипса.  Число   называют эксцентриситетом эллипса. Две прямые   называются директрисами эллипса.  Точки пересечения эллипса с осями симметрии   называют вершинами эллипса.