86. У чому суть методів мережевого планування і управління?

Серед сучасних методів оптимізації і керування виробничими процесами значна роль належить мережевим методам. Широке коло задач математичного програмування можна подати в мережевому вигляді. Особливо це стосується транспортних задач, які мають цілком природну інтерпретацію як мережеві задачі, бо вони пов’язані з певною мережею транспортних маршрутів (доріг, залізничних, водяних шляхів, маршрутів повітряних трас, трубопроводів тощо). У цьому параграфі буде розглянуто кілька типових мережевих задач математичного програмування.

Назвемо графом будь-яку систему відрізків (прямолінійних чи криволінійних), у певний с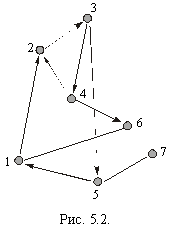 посіб з’єднаних між собою (рис. 5.2).

Названі відрізки, якщо їм приписано напрям, називаються дугами графа; надалі позначатимемо їх , наприклад: — відрізок, що з’єднує точку 1 з точкою 2 (рис. 5.2).

Точки, що є кінцями або початками дуг графів, в яких можуть з’єднуватись дві дуги або більше, називаються вершинами графа: кожна з вершин позначається певним номером (натуральним числом: 1, 2, 3, 4, ...), наприклад, точки 1, 2, 3, — вершини (рис. 5.2).

Отже, кожній дузі відповідає впорядкована пара вершин , де перший індекс і означає початок дуги (вхід), другий індекс j — кінець дуги (вихід); тим самим задано орієнтацію (напрям) дуги, що геометрично зображається стрілкою в напрямі від початку до кінця дуги.

Дуги та називаються симетричними, або взаємними, наприклад: (2, 4) і (4, 2).

Ребром (або ланкою) графа називається ненапрямлений відрізок, що зображає дугу. Позначимо ребра символами , наприклад [5, 7] — ребро; тоді як для відповідних дуг ця рівність не справджується: .

Мережею (або сіттю) називається граф, елементам якого (дугам, вершинам, деяким їх сукупностям) поставлені у відповідність деякі параметри, що визначають їх властивості.

Такими параметрами можуть бути, наприклад, пропускні здатності шляхів, величини запасів чи потреб у певних пунктах — вершинах графа тощо.

Шляхом у графі називається послідовність дуг , кінець кожної з яких збігається з початком наступної, крім останньої (або початок кожної з яких збігається з кінцем попередньої, крім першої), тобто ..., .

Шлях зручно позначати послідовністю вершин, через які він проходить, тобто . Прикладом шляху є послідовність таких дуг (1, 2), (2, 3), (3, 5) або (1,2, 3, 5).

Контуром називається шлях, початкова вершина якого збігається з кінцевою, наприклад (1, 2), (2, 3), (3, 5), (5, 1) = (1, 2, 3, 5, 1).

87. Принцип оптимальності

З викладених у попередніх параграфах міркувань можна висновувати, що для прийняття оптимального рішення на k-му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від параметра етапу , визначеного на попередньому кроці.

Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так:

Оптимальний розв’язок багатокрокової задачі має ту властивість, що яким би не був стан системи в результаті деякої кількості кроків, необхідно вибирати управління на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.

Доведемо справедливість такого твердження, міркуючи від супротивного. Нехай маємо задачу на максимізацію функції і вектор є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.

Принцип оптимальності еквівалентний твердженню, що вектор повинен бути оптимальним планом -крокового процесу -вимірної задачі з початковим параметром стану , що дорівнює . Припустимо протилежне, тобто що вектор не є оптимальним планом відповідного процесу, а ним є якийсь інший план . Тоді дістанемо:

,

але

,

що суперечливо. Отже, принцип оптимальності доведено.