67.Сформулювати критерій оптимальності в процедурі симлексу і дати його екон.Інтерпретацію.

Симплексний метод уможливлює направлений перебір опорних планів, тобто перехід від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням функціонала. Позначимо через коефіцієнт функціонала, що відповідає вектору , та (їх називають оцінками відповідних векторів плану) . Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану розклад всіх векторів у даному базисі задовольняє умову: ,

68.Критерій оптим.для т.з. Отже, як наслідок другої теореми двоїстості для транспортної задачі отримали необхідні та достатні умови оптимальності плану.Теорема (умова оптимальності опорного плану транспортної задачі). Якщо для деякого опорного плану Х^* = (x_ij*) існують числа u_i та v_j, для яких виконуються умови:1) u_i + v_j = c_ij,2) u_i + v_j  c_ij,

x_ij > 0, x_ij = 0 x_ij = 0

для всіх та , то він є оптимальним планом транспортної задачі.

71. Сформулювати основні етапи алгоритму методу множників Лагранжа для завдань на умовний екстремум.

Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:

(8.6)

за умов:

, (8.7)

де функції і мають бути диференційовними.

Задача (8.6), (8.7) полягає в знаходженні екстремуму функції за умов виконання обмежень .

Переходимо до задачі пошуку безумовного екстремуму. В літературі [13, 28] теоретично доведено, що постановки та розв’язання таких задач еквівалентні.

Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:

(8.8)

де — деякі невідомі величини, що називаються множниками Лагранжа.

Знайдемо частинні похідні і прирівняємо їх до нуля:

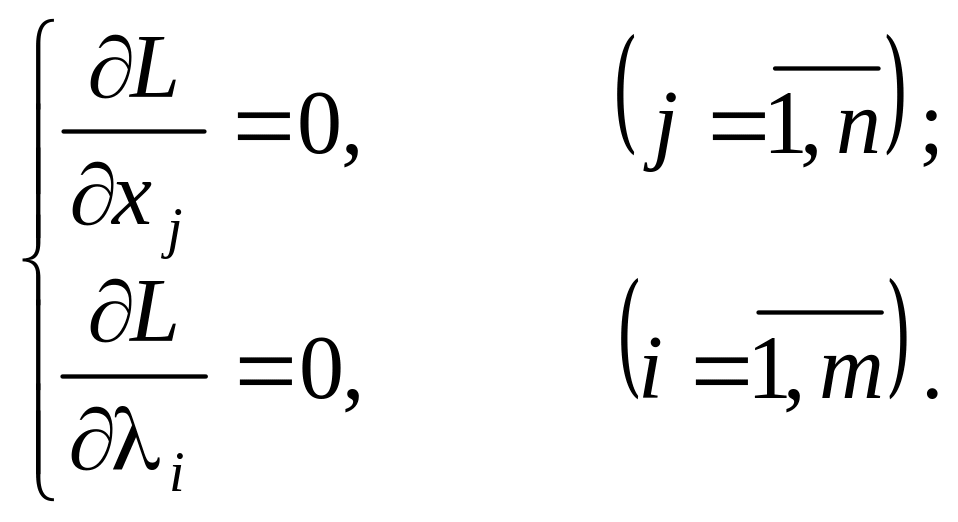
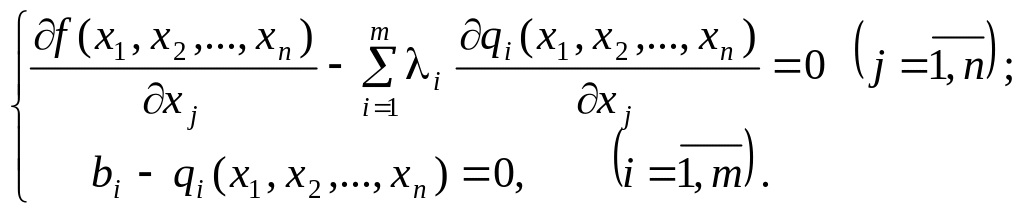(8.9)

Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування.

Система (8.9), як правило, нелінійна.

Розв’язками її є і — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6), (8.7) або можуть бути точками перегину (сідловими точками).

Для діагностування стаціонарних точок і визначення типу екст­ремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій існують другі частинні похідні і вони неперервні).

Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функ­цією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю :

де О — матриця розмірністю , що складається з нульових елементів,

Р — матриця розмірністю , елементи якої визначаються так:

,

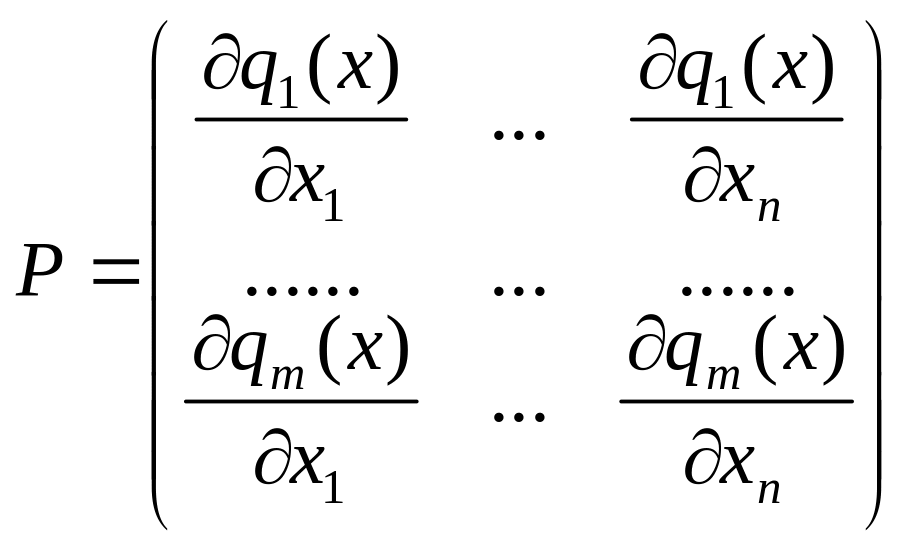— транспонована матриця до Р розмірністю ,

Q — матриця розмірністю виду:

, де .

Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати і .

1. Точка є точкою максимуму, якщо, починаючи з голов­ного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником .

2. Точка є точкою мінімуму, якщо, починаючи з головного мінору порядку (m + 1), знак наступних (n – m) головних мінорів матриці Н визначається множником .