Коефіцієнт є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору. Безвипромінювальні переходи

Крім випромінювальних переходів, пов'язаних з поглинанням і випромінюванням кванта енергії, у системі квантових часток можливі безвипромінювальні переходи, при яких енергія атома передається іншим атомам або навколишньому середовищу (виникають при зіткненні атомів і молекул у газі, як один з одним, так і з електронами або стінками посудини, переходи в твердому тілі при взаємодії з коливаннями кристалічної решітки й т.д.).

У результаті такої взаємодії атом, іон або молекула переходить зі стану n у стан m або навпаки без випромінювання кванта й без його участі (малюнок 5а,б).

а) б)

Рис. 5

Ймовірність безвипромінювального переходу з верхнього рівня на нижній прийнято позначати _nm, з нижнього на верхній _mn. Ймовірності безвипромінювальних переходів між рівнями n m зв'язані рівністю

.

Середній час життя атома .

Якщо квантова частинка робить перехід зі збудженого стану n, у результаті різних процесів (спонтанних, індукованих, безвипромінювального переходів), що характеризується часом життя ₁=1/А_mn, ₂ =1/B_mn(), ₃=1/_mn і ці процеси статистично незалежні, то середній час життя частки в стані n пов'язане із часами життя для інших процесів співвідношенням

.

Зв'язок між коефіцієнтами ейнштейна

Розглянемо сукупність атомів (молекул), які знаходяться в термодинамічній рівновазі зі стінками оточуючого об’єму при температурі Т.

Нехай на рівні Е_m знаходиться N_m частинок, а на рівні Е_n - N_n частинок.

Тоді число поглинутих квантів за інтервалом dt буде

.

Число квантів світла, які будуть випромінені в результаті спонтанних переходів:

,

а кількість квантів світла, які випущені в результаті вимушеного випромінювання

.

При термодинамічній рівновазі ансамбль квантових часток не втрачає і не здобуває енергію.

Отже, умова термодинамічної рівноваги означає, що загальна кількість квантів світла, які випромінені системою, дорівнює числу поглинутих квантів світла:

або (1)

Загальне число переходів визначається числом часток на рівнях енергії.

При тепловій рівновазі розподіл часток по рівнях підкоряється формулі Больцмана

, (2)

де g₁ і g₂ – статистична вага рівнів 1 і 2 (для невироджених рівнів gn = gm = 1);

k - постійна Больцмана 1,38*10^-23 Дж/K.

Частки розглянутого ансамблю перебувають у поле їхнього власного випромінювання, щільність енергії якого в одиничному спектральному інтервалі становить ().

Це поле индуцирует переходи з верхнього стану в нижнє й назад. Імовірності цих переходів пропорційні ()

. (3)

Комбінуючи (2) і (3) з умови термодинамічної рівноваги (сумарне число квантів, що випускаються системою дорівнює числу квантів світла, що поглинаються,)

. (4)

Можна знайти співвідношення між коефіцієнтами A_nm, B_nm, B_mn.

У рівнянні (4) прирівняний друг до друга повні числа переходів знизу нагору (ліворуч) і зверху вниз (праворуч).

Це рівняння дозволяє чітко знайти щільність енергії поля випромінювання розглянутої рівноважної квантової системи:

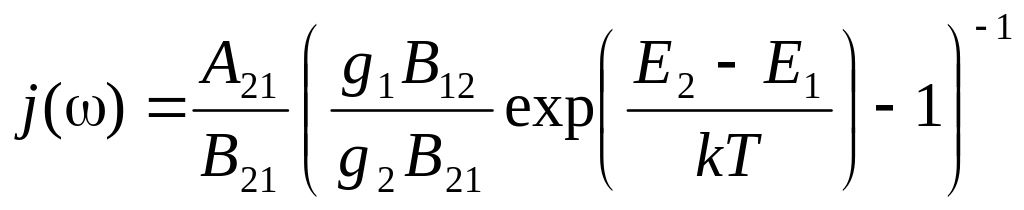. (5)

Звідси випливають важливі наслідки!

Ейнштейн постулировал, що випромінювання, що випускається й поглинає при рівноважних переходах між енергетичними станами розглянутої рівноважної квантової системами, описується формулою Планка для рівноважного випромінювання абсолютно чорного тіла

. (6)

Іноді формулу Планка записують не для (((), а для (((), при цьому ((()=((()/2(.

Порівнюючи ці дві формули з урахуванням умови Бору (Е_2-І1 = ) Одержуємо:

g₁B₁₂=g₂B_21. (7)

Це співвідношення говорить про равновероятности індуковані випромінювання й поглинання (у перерахуванні на одне невырожденное стан).

А ймовірність спонтанного випромінювання пропорційна коефіцієнту Ейнштейна для індукованого випромінювання:

. (8)

Імовірність спонтанного переходу в одиницю часу пов'язана з імовірністю змушеного переходу між станами співвідношенням

, =2πν, ν=с/λ с-швидкість світла 3*10⁸ м*с^-1 (9)

а ймовірності індукованих переходів з випромінюванням (nm) і поглинанням (mn) енергії рівні між собою, тобто B_nm = B_mn.

Коефіцієнт є число типів коливань в одиничному об'ємі й в одиничному інтервалі частот для вільного простору.

Таким чином, установлений зв'язок між коефіцієнтами Ейнштейна, але не саме їхнє значення. Це буде зроблено пізніше.

Можна тепер записати, що повна ймовірність переходу вниз для збудженої частки з випущенням квантів випромінювання дорівнює

. (10)

Істотно, що пропорційно В₂₁, і, отже, там, де заборонені індуковані переходи, не може бути й спонтанного випромінювання й навпаки, де немає спонтанного випромінювання, там не може бути індукованого випромінювання.

Рівноважне випромінювання всього ансамблю часток стосовно кожної із часток виступає як зовнішнє електромагнітне поле, що стимулює поглинання або випромінювання часткою енергії залежно від її стану.

Тому співвідношення (8-10), отримані при розгляді умов рівноваги, справедливі й для випадку квантової системи, що перебуває в поле зовнішнього випромінювання.

Ще одне зауваження. З (9) треба, що ймовірність спонтанних переходів сильно залежить від частоти - як куб частоти.

Звідси треба, що в області СВЧ, де працюють парамагнітні мазери, роль спонтанних переходів невелика й, як наслідок, - дуже низький шум таких підсилювачів.

В оптичному діапазоні частот роль спонтанних переходів різко зростає, вони є джерелом шумів, причиною дуже малих часів життя збуджених станів, що утрудняє, а іноді й унеможливлює роботу підсилювачів і генераторів.

У всякому разі, в оптичному й белее короткохвильових діапазонах довжин хвиль зі спонтанними переходами доводиться вважатися істотно. Отже з ростом частоти ймовірність спонтанного переходу різко зростає.

В загальному випадку, якщо спустошення збудженого стану m проходить за рахунок різних незалежних процесів, які характеризуються сталими часу τ_1, τ_2,…... τ_∞ або ймовірностей середній час життя атома у збудженому стані m:

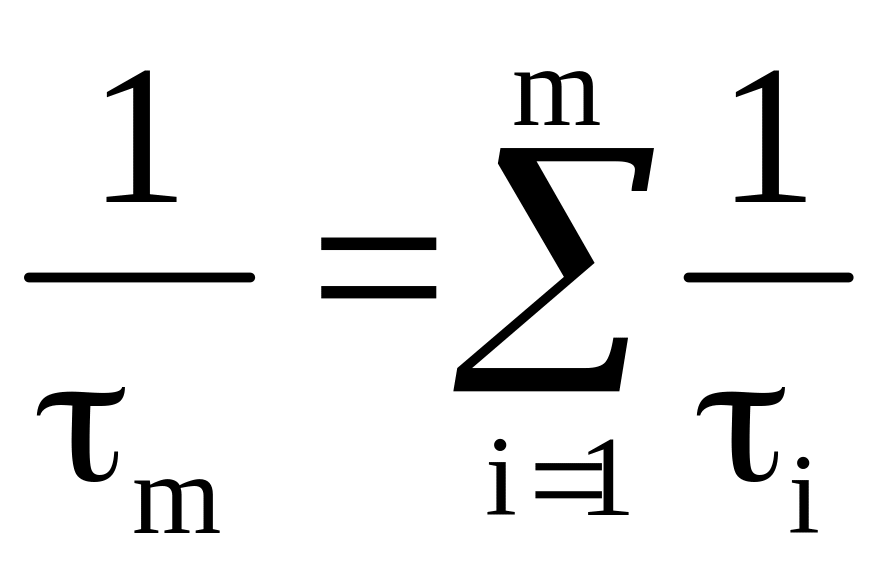
Ймовірність переходу пов’язана з відповідним матричним елементом і для оптичних переходів цей зв'язок найбільш виразно проявляється при порівнянні класичного і квантового осциляторів. При цьому виконується дипольне наближення.