106.Применение рядов в приближенных вычислениях. Оценка точности вычислений

Разложение ф-ций в степенные ряды позволяет применять эти ряды для приближенного вычисления значений ф-ций, определенных интегралов, решения дифференциальных уравнений. Для вычисления приближенного значения ф-ции в ее разложении в степенной ряд сохраняют первые n членов, а остальные члены отбрасывают. Чтобы получить погрешность найденного приближенного значения, нужно оценить сумму отброшенных членов. Если данный ряд знакопостоянный ,то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. Если ряд знакопеременный и члены его удовлетворяют признаку Лейбница, то ипользуется оценка

∆<|u_n+1|, где u_n+1 – первый из отброшенных членов, т.е. ошибка приближенного вычисления не превосходит абсолютной величины первого из отброшенных членов.

71. Осн св-ва опред интеграла

Значение о.и. не зависит от обозначения переменной интегрирования.

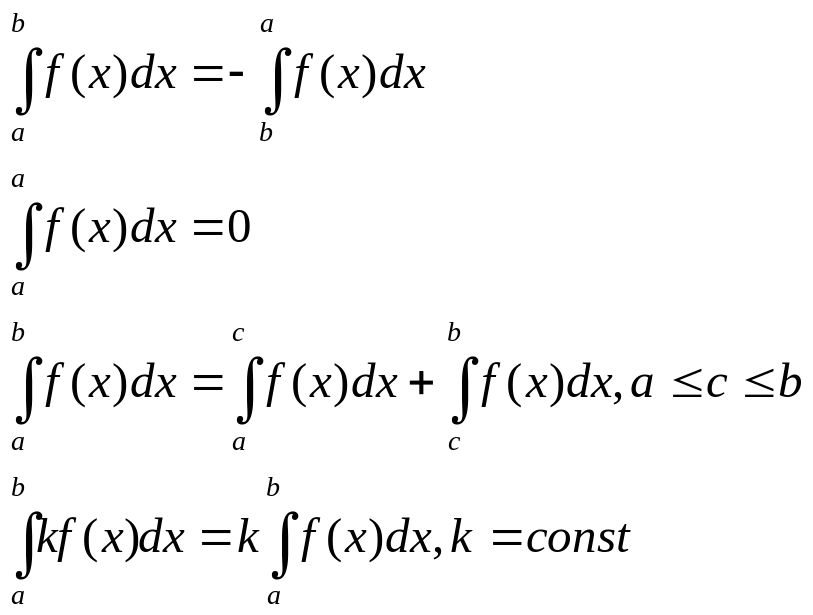
Если , x € [a;b]

99. Знакочеред ряды. Достат усл-е сх-ти (теорема Лейбница). Абсол и условная сходимость.

О. Ряд вида (1)

наз знакочеред-ся.

Признак Лейбница (сх-ть знакочер ряда).

Для того, чтобы ряд (1) сх-ся достаточно, чтобы абсол значения убывали и →0 при возрастании n, т.е.

О. Если ряд, сост из абсол значений величин сх-ся, то ряд наз абсолютно сходящимся.

Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся.

Док-во:восп-ся 1 признаком сравнения

Рассм-м ряд

- ряд из абсол значений величин

Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно.

О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся.

Интегрирование рациональных дробей

1. Многочленом степени n наз-ся выражение вида a₀+a₁x+a₂x²+…+a_nxⁿ=P_n(x)

Рациональной дробью наз-ют отношение двух многочленов вида

При n=0 вычисление интеграла никаких трудностей не представляет

Интерес представляют рациональные дроби, у кот. n>0

При этом будем рассматривать дроби, у кот. m<n

Если m>=n, то применяют процедуру деления многочленов уголком

2. Интегрирование простейших дробей

I . x-a=t dx=dt

I I. x-a=t dx=dt

III. Интегрирование выражений, сод-х квадратный трехчлен

x+p/2=t dx=dt a²= или

IV.

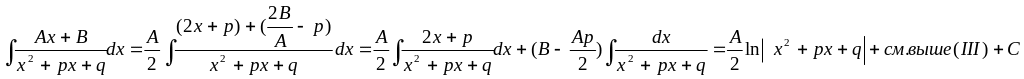
V. p²/4-q>0

p²/4-q<0

70. Определение опред. Интеграла

Пусть зад ф у=f(x), кот непрер на некот. замкнутом инт-ле [a,b].

Разбиваем инт-л [a,b] на n частей; абсциссы точек дел-я a=x₀<x₁<x₂<…<x_i-1<x_n-1<x_n=b обозн x₁,x₂,…x_n. Кажд частичный инт-л обозн ∆x₁=x₁-x₀, ∆x₂=x₂-x₁, ∆x_i=x_i-x_i-1, ∆x_n=x_n-x_n-1. В каждом частичном инт-ле ∆x_i , i= 1;n выберем т. и выч-м ﻉ_I , y=f(x), y=f(ﻉ₁) , f(ﻉ₂) , … f(ﻉ_i) ,… f(ﻉ_n) Cост-м произв-е f(ﻉ₁)∆x₁, f(ﻉ₂)∆x₂ , … f(ﻉ_i)∆x_i ,… f(ﻉ_n)∆x_n. Кажд из этих произв-й предст собой полоску шириной ∆x_i и высотой f(ﻉ_i).

О1. Сумма f(ﻉ₁)∆x₁+ f(ﻉ₂)∆x₂ + … f(ﻉ_i)∆x_i +… f(ﻉ_n)∆x_n=∑ f(ﻉ₁)∆x₁ наз интегр суммой ф. f(x) на инт-ле [a,b]. С геом. точки предст собой S ступенчатой фигуры.

Обозн наиб. из разностей ∆x₁₌ x_i-x_i-1 через ОХ. Тогда имеет место определение 2.

О2. Сущ кон предел интегр ∑, т.е. f(ﻉ₁)∆x₁ и он не зав-т от СП-ба разбиения инт-ла [a,b] и выбора точек ﻉ₁ на частичных инт-лах ∆x_i, то этот предел наз опред интегралом ф. f(x) на [a,b] и обозн

Т. Для всякой непрер ф-и интеграл сущ.

Геом. смысл опред. интеграла.

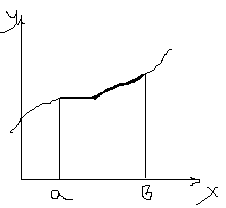
Опред интеграл опред-т точное зн-е S криволин тр-и.