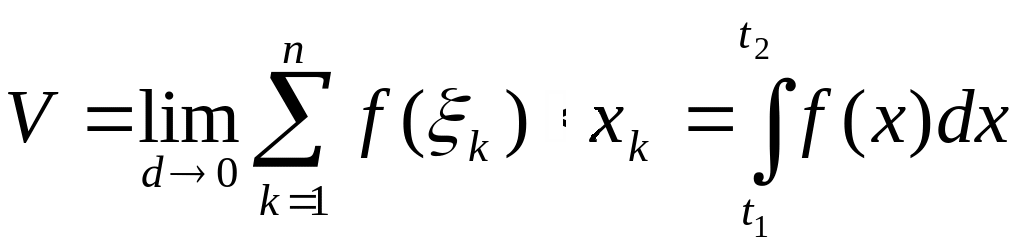- •1.Матрица – прямоугольная таблица чисел, содержащая m строк одинаковой длины(или n столбцов одинаковой длины).
- •2.Умножение матрицы на число
- •3.Умножение матриц
- •2 Матр а и в соглас-е, если число строк матр а равно числу столбцов матр в, и наоборот.
- •9. Система m-линейных ур-й с n неизв-ми. Матричная запись системы. М-д обр матрицы. М-д Крамера.
- •10. Метод Гаусса. Эквив преобраз-я систем. Базисные и своб неизвестные. Критерий совместности.
- •Перестановка уравнений системы.
- •По исх сист записываем расшир матр системы.
- •Amn ≠ 0 – система имеет единственное решение
- •11. Системы линейных однородных уравнений.
- •13.Вектор на плоскости и в простр-ве. Лин опер-и над в-ми, их св-ва. Базис на пл-ти и в простр-ве. Ортонормированный базис.
- •21.Уравнение прямой-уравнение, которому удовлетворяют координаты любой точки этой и только этой прямой.
- •23.Углом между двумя прямыми называется любой из двух углов, образованных прямыми при их пересечении.
- •25.Расстояние от точки до прямой
- •26,27.Окружность
- •28.Гипербола, ее характеристики, геометрические свойства
- •29.Где идут буквы с нулями-это значит,например x0,только в уменьшенном варианте где s,n-это вектора ,сверху палочку подрисуйте¯; √- этот корень всегда доводите до конца выражения
- •30.Плоскость.Условие параллел-ти и перпендик-ти
- •1 Из спос-в зад-я пл-ти через зад точку m0(x0,y0,z0) с заданным нормальным вектором n(a;b;c)
- •31.Расстояние от точки до плоскости.Угол между плоскостями
- •32.Пр линия в пр-ве.Параметрич ур-е прям.Канонич ур-е пр
- •36.Предел числовой последовательности (чп).
- •X1, x2,…xn,…-числ послед.(1), xn-общ член чп.
- •37.Понятие ф-и. Сп-бы задания ф-й, оп-ции над ними. Обр ф-ия. Элемент ф-ии, их классификация.
- •39.Осн теоремы о пределах. Замечат пределы.
- •40.Непрерывность функции в точке. Точки разрыва и их классификация.
- •1)Первая теорема Вейерштрасса
- •2) Вторая теорема Вейерштрасса
- •3) Теорема Больцано-Коши о промежут.Значении
- •43.Произв. Ф-ции. Геометр., механ., экон. Смысл произ-ной. Эласт-сть ф-ции, ее экон приложение.
- •45.Производная показательной неявной функции. Производные высших порядков:
- •47.Теорема Лагранжа. Правило Лопиталя.
- •55.Понятие функции многих переменных
- •56.Пределы и непрерывность ф-ций двух переменных
- •57.Частные производные первого и второго порядка
- •58.Полный дифференциал функции 2-х переменных и его приложения
- •2) , Экстр-ма в т. Нет
- •3) , Треб-ся доп исслед-е
- •1) Выбор точки ; 2) устан-ть вид вычисл-мой ф-и
- •2) , Экстр-ма в т. Нет
- •3) , Треб-ся доп исслед-е
- •62.Наибольшее и наименьшее значение функции 2-х переменных
- •1 Из алгоритмов реш-я этой задачи сводится к след
- •II этап
- •64,65.Неопред интеграл, первообразная и их св-ва.
- •67.Интегрир-е путем замены переменной(подстановкой)
- •72.Определенный интеграл с переменным верхним пределом
- •73.Формула Ньютона-Лейбница (вывод)
- •74.Интегрирование по частям и замена переменной в определенном интеграле
- •2)Определение средних значений
- •Издержек производства
- •2)И. На конечном промежутке
- •82.Дифференциальное уравнение(ду)
- •83.Ду 1го порядка
- •2)Имеет частную произв-ю по y для любой точки
- •92,93Лин неоднор ду 2-го порядка с пост коэфф-ми.
- •94.Числовой ряд и его сходимость.
- •2.Сумма ряда. Примеры сходящихся и расходящихся рядов. Гармонический ряд (док-во его расходимости).
- •96.Свойства сходящихся рядов
- •97.Достат признаки сх-ти ряда с положит членами.
- •98. Признаки сравнения рядов
- •101.Теорема Абеля.
- •103.Свойства степенных рядов .
- •2) Степенной ряд можно дифференцировать бесконечное число раз.
- •3) На произвольные функциональные ряды данная теорема без специальных предположений не распространяется.
- •104.Ряды Тейлора и Маклорена.
- •105.Разложение некоторых елементарных ф-ций в степенные ряды
- •106.Применение рядов в приближенных вычислениях. Оценка точности вычислений
- •99. Знакочеред ряды. Достат усл-е сх-ти (теорема Лейбница). Абсол и условная сходимость.
- •Определение опред. Интеграла
67.Интегрир-е путем замены переменной(подстановкой)
М-д подстановки
∫ f(x)dx=
[x=φ(t),t=ψ(x),dx=φ’(t)dt]
=∫f(φ(t)φ’(t)dt
f(x)dx=
[x=φ(t),t=ψ(x),dx=φ’(t)dt]
=∫f(φ(t)φ’(t)dt
Если интеграл непосредственно не вычисляется,можно применить метод,кот. состоит в след.:
-вводится новая переменная
x=φ(t),где t=ψ(x) явл. обратной по отношению к φ(t), dx=φ’(t)dt- дифференциал ф-ции x=φ(t)
Если подстановка выбрана удачно, то интеграл, получ в правой части, вычисляется проще, чем в исходной.
Если ф-ция x=φ(t) непрерывна и монотонна,то обратн. t=ψ(x) всегда сущ.
Вычислив интеграл в правой части по t,следует вернуться к переменной x
∫f(ψ(x)) φ’(x)dx=∫f(t)dt, где t=ψ(x)
1 ∫f(ax+b)dx= ax+b=t, x=(t-b)/a
∫f(ax+b)dx= ax+b=t, x=(t-b)/a
dx=1/a dt
=∫f(t)1/a dt=1/a ∫f(t)dt=1/a F(t)+C=
=1/a F(ax+b)+C
2
 ∫ f’(x)/f(x) dx= ln f(x) +C
∫ f’(x)/f(x) dx= ln f(x) +C
3 ∫ df(x)/f(x) = ln f(x) +C
Метод интегрирования по частям
Задано: U=U(x), V=V(x),известно: d(UV)=VdU+UdV
проинтегрируем обе части уравнения:
∫ d(UV)= ∫ VdU+ ∫ UdV
UV=∫ VdU+ ∫ UdV=> ∫UdV=UV-∫VdU- ф-ла интегр-я по частям
Смысл ф-лы интегр-я по частям сост в след.: подинтегр выраж-е UdV разб-ся на 2 части т. о.,чтобы интеграл в правой части вычислялся проще,чем исходный.
Основные классы ф-ций,интегрируемых по частям:
1 ∫ lnm(x)dx, ∫arcsinmxdx, ∫arccosm xdx,∫arctgm xdx
2 ∫Pn(x)lnaxdx,∫Pn(x)eaxdx,∫ Pn(x)sinaxdx,
∫Pn(x)cosaxdx
3 ∫eaxsinbxdx,∫eaxbxdx
4 ∫ (x²+a²)½dx, ∫(a²- x²)½dx, ∫ dx/(x²+a²)k
72.Определенный интеграл с переменным верхним пределом
Ф-я
вида
![]() ,
где x
,
где x![]() наз интегралом c
перем верхним пределом.
наз интегралом c
перем верхним пределом.
Т:
Если
![]() непрер на
непрер на
![]() ,
то произв-я ф-и
, сущ в каждой точке
,
то произв-я ф-и
, сущ в каждой точке
![]() на
, причем
на
, причем
![]()
73.Формула Ньютона-Лейбница (вывод)
Т: Если
непрерывна на
, справедлива ф-ла Ньютона-Лейбница:
![]()
ВЫВОД ФОРМУЛЫ:
Рассм-м
, т.к.
,
то![]() -
первообразная для
.
Но
-
первообразная для
.
Но
![]() ,
также первообразная. Это значит что
имеет место следующее равенство :
,
также первообразная. Это значит что
имеет место следующее равенство :![]()
![]()
Подставим верхнюю границу:
![]()
![]() подставами
вместо
подставами
вместо
![]() :
:
![]() в
силу 1-го свойства, что значении
определенного интеграла независит от
обозначения переменной интегрирования,
запишем:
в
силу 1-го свойства, что значении
определенного интеграла независит от
обозначения переменной интегрирования,
запишем:
![]()
74.Интегрирование по частям и замена переменной в определенном интеграле
Формула интегрирования по частям для определенном интеграла.
Пусть
заданны
![]() тогда имеет место интегрирование по
частям:
тогда имеет место интегрирование по
частям:
![]() →
→
![]()
Замена переменной в определенном интеграле.
Пусть
непрерывна на
,
а
![]() непрерывна на
непрерывна на
![]() .
Вместе со своей производной
.
Вместе со своей производной
![]() ;
причем
;
причем
![]() ,
и сложная функция
,
и сложная функция
![]() непрерывна
на
непрерывна
на
![]() ,
тогда справедливо формула замены
переменной для определенного интеграла:
,
тогда справедливо формула замены
переменной для определенного интеграла:
![]()
75-77.Геометрич приложения определенного интеграла
Вычисление площадей плоских фигур:
1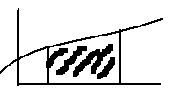 .
на
и
.
на
и
![]()
![]()
2.
на
и
![]()

![]()
3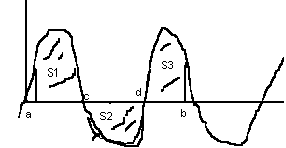 .
на
график имеет вид
.
на
график имеет вид
![]()
![]()
4.
даны две функции:
и
![]() на промежутке
на промежутке
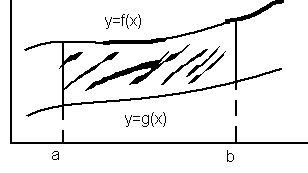
![]()
5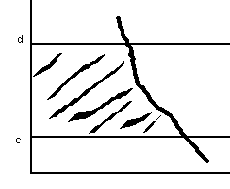 .
.
![]() на промежутке
на промежутке
![]() то получаем
то получаем
![]()
6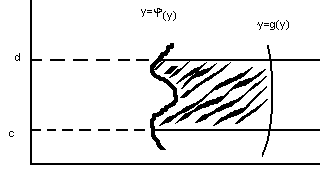 .
и
.
и
![]() на промежутке
на промежутке
![]() (графики ориентированны на
(графики ориентированны на
![]() )
)
![]()
7.вычисление
площади плоской фигуры заданной системе
к оординат.
В полярной системе точка это пара чисел
оординат.
В полярной системе точка это пара чисел
![]() ,
любая линия равна
,
любая линия равна
![]() .
.
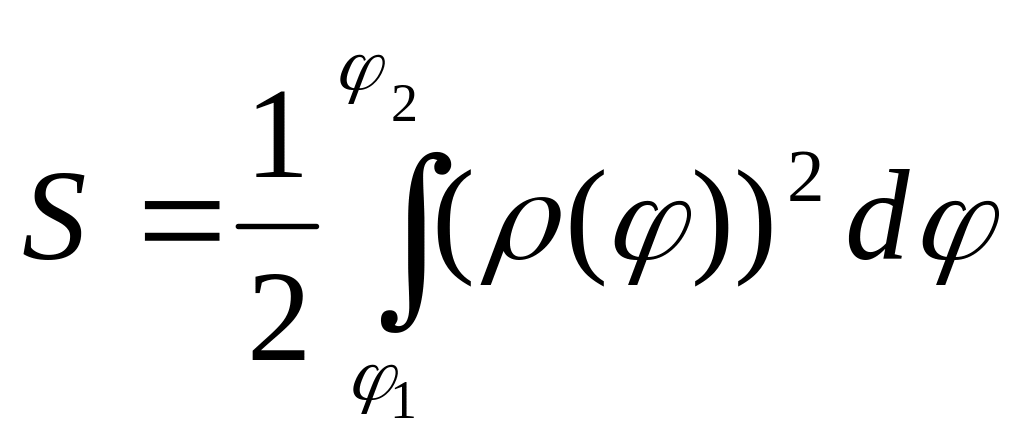
Уравнение Лемниската-Берлуни
![]()
9. Вычисление длины дуги кривой. Пусть заданна на .
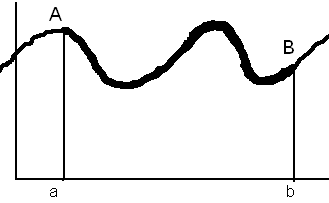
![]()
78-80.Определенный интеграл в экономических и физических задачах
1)Вычисление
объема произведенной продукции. Известно,
что производительность труда в течение
рабочего дня меняется. Предположим, что
известна непрерывная функция f(x),
которая характеризует измерение
производительности от времени ![]() .
Определить объем продукции, произведенной
рабочим за промежуток времени от t1
до t2.
Решение. Искомый объем можно рассматривать
как сумму объемов продукции, произведенной
за бесконечно малые отрезки времени.
Возьмем разбиение xk
отрезка t1,t2.
В этом случае предел интегральных сумм
.
Определить объем продукции, произведенной
рабочим за промежуток времени от t1
до t2.
Решение. Искомый объем можно рассматривать
как сумму объемов продукции, произведенной
за бесконечно малые отрезки времени.
Возьмем разбиение xk
отрезка t1,t2.
В этом случае предел интегральных сумм
![]() при
диаметре d0
разбиенийxk
отрезка t1,t2
даст искомый объем продукции. Этот
предел существует, так как функция f(x)
непрерывная,
т.е.
при
диаметре d0
разбиенийxk
отрезка t1,t2
даст искомый объем продукции. Этот
предел существует, так как функция f(x)
непрерывная,
т.е.