1.Матрица – прямоугольная таблица чисел, содержащая m строк одинаковой длины(или n столбцов одинаковой длины).

a11 a12 … an1

A= a21 a22 … an2

… … … …

am 1 am2 … amn

a1i a2i …ain-i=1,m – i-тая строка

a1j a2j … amj-j= 1,n – j-тый столбец

Элементы, стоящие по диагонали, идущей из верхнего левого угла, образуют главную диагональ; из верхнего правого – побочную.

Матрицы равны между собой, если равны их соответствующие элементы.

Матрица, у которой число строк равно числу столбцов, называется квадратной.

Матрица размера n·n - матрица n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю – диагональная.

Диагональная матрица у которой каждый элемент главной диагонали равен единице, единичная.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, - нулевая.( обозначается буквой О)

Матрица, содержащая один столбец или одну строку – вектор.

2.Умножение матрицы на число

Пусть задана матрица А=aij i=1,m; j=1,n; α принадлежит R. Чтобы умножить матрицу А на число α, нужно кадый Эл-т матрицы умножить на это число α .

С=(αaij)

Сложение матриц

Пусть заданы А=aij и В=bij одинаковой размерности i=1,m; j=1,n. Тогда суммой двух этих матриц называется матрица С=сij. Другими словами, нужно сложить соответствующие эл-ты. Кратко: С=А+В

Св-ва:

1. А+В=В+А

2. А+(В+С)=(А+В)+С

3. А+0=А

4. А-А=0

5. 1·А=А

6. α·(А+В)=αА+αВ

7. (α+β)·А=αА+βА

8. α·(βА)=(βα)·А

3.Умножение матриц

2 Матр а и в соглас-е, если число строк матр а равно числу столбцов матр в, и наоборот.

Оп-ция умн-я матриц определена только для соглас. матриц.

Кв матрицы одного и того же порядка и одной и той же размерности всегда согласованны.

Пусть задана матр А=aik i=1,m; k=1,n и матр В=bkj k=1,m; j=1,n. Тогда произв-ем А на В наз. матр С такая, что сik=ai1·b1k+ ai2·b2k +…+ ain·bnk, где i=1,m; k=1,n, т.е. эл-т i-той строки и k-того столбца матрицы произв-ия С равен ∑ произв-ий эл-ов i-той строки матр А на соответствующие эл-ты k-того столбца матр В.

Если выполняется равенство АВ=ВА, то матрицы А и В наз. перестановочными (коммутирующими)

Матр,получ. из данной заменой кажд ее строки столбц с тем же номером,наз. транспон-ой к данной.

Св-ва умножения:

1.А·(ВС)=(АВ)С

2. А(В+С)=АВ+ВС

3. (А+В)С=АС+ВС

4. α(АВ)=(αА)В

Св-ва транспонирования:

1.(А+В)^т=А^т+В^т

2. (АВ)^т=В·А^т

3. (А^т) ^т= А

Квадратная матрица А, которая не меняется при транспонировании, - симметричная.

Е сли матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.

А= 2 5 -2

5 -7 3

-2 3 1

4.Опред-ль 1,2,3 порядков.

Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем следующим образом:

1. n=1. A=(a₁); det A=a₁

2. n=2.

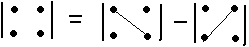
3. n=3.

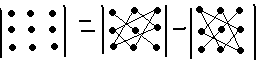
6.Свойства определителей.

1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то det

этой матрицы равен 0

2)При транспонировании матрицы её определитель не

изменяется: (detА =detА')

3) При перестановке местами 2-х строк или столбцов матрицы её

определитель меняет свой знак на противоположный

4) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0.

5)Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0.

6) Определитель матрицы не изменяется если к элементам одной строки (или столбца) прибавить элементы другой строки (или столбца), умноженные на одно и то же число

7) Общий множитель строки или столбца можно выносить за знак определителя

8) Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

Доказательство – проверкой.

9) det верхней треуг. матрицы = произведению диагональных эл-тов.

10) det A*B=detA*detB

7.Обратная матрица

Обр матр — такая матр A^-1, при умн-и на кот исходная матрица A даёт в результате единичную матрицу E:

AA⁻¹ = A⁻¹A = E

Теорема : для того, чтобы для кв.м.А сущ-ла обр, дост-но чтобы опр-ль этой м. был отличен от 0.(Кв матр обратима тогда и только тогда, когда она невырожденная, т.е. её опр-ль не равен 0. Для некв матриц обр матриц не сущ-т.)

Доказательство:

Необходимость. Пусть для матрицы A существует обратная матрица A^-1.

detA^-1*A=detE => detA≠ 0.

Д остаточность.

по м.А строим А^*

где А^* - м. алгебраических дополнений А^*

транспонируем полученную матрицу: (А^*)^Т=

найдем А* (А^*)^Т=С, Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

следовательно А* (А^*)^Т=detA*E => =>

Сформ-м правило нах-я обр матр на примере матр А.

1. Находим опр-ль матр. Если Δ ≠0, то матр A^-1 сущ-т.

2. Составим матрицу A^* алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице A^* элементом i - ой строки и j - го столбца будет алгебраическое дополнение Aij элемента aij исх матрицы.

3. Транспонируем матрицу A^* и получим A^*T

4)

5 проверка A^-1*A=E

8.Минор к-го порядка матрицы. Базисный минор матр. Ранг матр и его св-ва. Теорема о ранге матр. Вычисление ранга.

А - прямоуг матрица размеров m*n.

Выбираем в матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель полученной матрицы называется минором k-го порядка матрицы А.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Наибольший из порядков миноров данной матрицы, отличный от нуля, называется рангом матрицы. (обозначается r(A))

нек. св-ва: 1) r(A)=0 => A=0

2)

3) ранг верхней треугольной м. = числу диагональных эл-тов гл. диагонали неравных нулю.

ранг трапециевидной матрицы= числу диагональных эл-тов главного базисного минора.

Ранг матр не изменится от след преобр-й, наз элемент преобраз-ми матрицы

: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой =0; - умножения строки на число, отличное от 0; - прибавления к эл-м строки соответствующих Эл-ов другой строки, умнож на одно и то же число. Ранг находят привидением её к треуг(трапециев) виду с пом этих элемент преобраз-ий

Теорема о ранге: наивысший порядок отличных от 0 миноров матрицы равен рангу этой матрицы