83.Ду 1го порядка

_{Имеют вид: y’=f(x,y) (1) F(x,y,y’)=0 (2)}

_{1) y’=f(x) dy/dx=f(x)}

_{dy=f(x)dx dy=f(x)dx y=f(x)dx}

_{2) y’=f(y) dy/dx=f(y)}

_{3) f(x)dx=f(y)dy ДУ с разделенными переменными f(x)dx=f(y)dy}

_{4)y’=f(x)gy или M(x)N(y)d(x)=K(x)L(y)d(y)}

_{ДУ с разделяющимися переменными}

_{Ур-е вида (4) реш по схеме:}

_{d(y)/d(x)=f(x)gy}

_{d(y)/g(x)=f(x)d(x)}

_{M(x)d(x)/K(x)=L(y)d(y)/N(y)}

_{5) y’=g(y/x) однородное ДУ 1го порядка (ф-ция вида f(αx,αy)=α}^k_g(x,y) наз однор ф-ция k-того порядка,αЄR)

реш с помощью подстановки

z=y/x y=zx y’=z’_xx+z

_{z’x+z=g(z) d(z)/(g(z)-z)=d(x)/x}

_{6) y’=f(ax+by) приводится к ур-ю вида (4) путем замены z=ax+by}

Теорема (Коши-Пикара). Пусть задано диффе­ренциальное уравнение вида y’=f(х,у), где f(x,y) — функция, заданная в области D, и в D заданы начальные условия M₀ (x_0,y₀)ЄD. В силу открытости области D можно указать числа а и b (а>0;-b>0) и для них замкнутую область : |х - x₀|≤ а, |у- у₀|≤b, такую, что D. Пусть в области ф-я z=f(x,y):

1)непрерывна, а значит, и ограничена, т.е. |f-(x, y)|≤H;

2)Имеет частную произв-ю по y для любой точки

М(х, у) и эта частная производная также огра­ничена в . Тогда сущ решение задачи Коши для начал условий М₀(х₀, у₀): y=(x), y₀ = (x₀), это решение единств, причем функция у=(х), оста­ваясь решением уравнения y⁽ⁿ⁾=f(x,y,y’,…,y^(n-1)) , задана, по крайней мере, на отрезке |х-x₀|≤h, где h=min(а, b/Н) и |(x)-y₀|≤b.

Доказательство этой теоремы не приводим.

Замечание. Поскольку реш-е у = (х) задано для |х - х₀| ≤h, т.е. –h+x₀≤x≤h+x₀, то если взять произвольную точку х₁ такую, что -h+x₀<x₁< h+x₀, и вычислить y₁ = (x₁), начальным условиям M₁(x₁,y₁) будет соответствовать то же решение у = (х); измениться в этом случае может лишь h в неравенстве |х — х₁|≤ h.

Общее решение. Пусть в DR² задано дифферен­циальное уравнение y’=f(х,у) и в любом D выполня­ются условия теоремы Коши — Пикара. Тогда однопараметрическое семейство функций

у = (х, С),непрерывно дифференцируемых по х и непрерывных по С в некоторой области Г(х, С), называется общим реше­нием уравнения в области D, если: 1) у =(х, С) явля­ется решением уравнения y’=f(х,у) для всех фиксированных С из некоторой области GR (на множествах X _с, таких, что для любых х  X _с и у =(х) (х, у)  D); 2) для любых начальных условий М₀(х₀, y₀)  D существует такое С₀  G, что y₀=(х₀, С₀), т. е. уравнение y’=f(х,у) дает реше­ние задачи Коши.

84-87.Осн классы ДУ 1 порядка, интегрир в квадратах.

1) ДУ с разделяющимися переменными – уравнения вида:

1. M(x)N(y) dx+K(x)L(y)dy=0

2. y`=f(x)g(y)

Решаются по схеме:

1. Делим на N(y)K(x):

M(x)/K(x)dx+L(y)/N(y)dy=0 и интегрируем обе части( в правой части вместо 0 будет С)

2. dy/dx=f(x)g(y). Обе части * на dx и / на g(y), получим:

dy/g(y)=f(x)dx и интегрируем обе части.

2) Однородные функции и однородные ДУ.

Функция f( )= *g(x,y) наз. Однородной функцией k-того порядка, R.

ДУ вида y`= f(x.y) наз. Однородным, если z=f(x,y) – однородная функйия нулевой степени, т.е. для любых t f(tx,ty)=f(x,y).Аналогично ДУ

P(x,y)dx+Q(x,y)dy=0 наз. Однородным, если P(x,y) и Q(x,y) – однородные функции одной степени.

3) Линейные ДУ 1 порядка.

Общий вид линейного ДУ 1 порядка:

y`+p(x)y=q(x)

1).если q(x) ,то y`+p(x)y=0 – однор. лин. ДУ 1 порядка

2)если q(x) 0, то ДУ – неоднородное линейное ДУ

Решение 2):

Y=uv, u=u(x), v=v(x); y`=u`v+uv`

U`v+uv`+ p(x)uv=q(x); u`v+u(v`+ p(x)v)=q(x);

_{dv/dx=-p(x)v,решаем и получим: v=}

_{подставим v в u`v=q(x) получим u=}

_{отсюда общее решение :}

_{y=uv=( )*}

88.ДУ 2 порядка, допускающие понижение порядка

1.y``=f(x), y`=p,где p=p(x); y``=p`; p`=f(x); dp/dx=f(x) отсюда p= ; y`= ; dy/dx= ; dy= )dx интегрируем,:

2. y``=f(x,y`), y`=p; p=p(x); y``=p`

p`=f(x,p(x)); интегрируем, p=

подставляем y`, все аналогично отсюда ответ:

y=

3. y``=f(y,y`), y`=p; p=p(y) – сложная ф-я y

y``=p`y`=p`p; p`p=f(y,p) или (dp/dy)*p(y)=f(y,p(y)).

P=

P заменяем на y` получим

x=

89. Комплексные числа, их геометрическая интерпретация, осн.св-ва.

Рассм. =-1

x1,x2 = ; =i – мнимая единица

=-1

z=a+bi; a,b , i- мнимая единица – комплексное число

a – действительная часть компл.числа, b- мнимая часть z

= a-bi – сопряженное z

z* =

Комплексные числа расп-ны на пл-ти, кроме оси ОХ

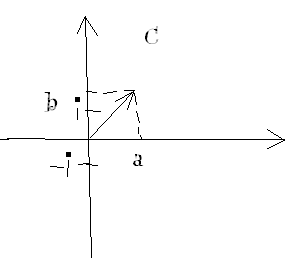z=a+bi

Любое компл число можно записать в тригон форме

90,91.Линейные однородные ДУ 2 порядка с постоянными коэфф-ми. Их нахождение.

Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:

(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция

Если r(x) =0, то

(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.

Ур-е вида (3) =0 – характерист.ур-е (1) и(2)

Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)

Возможны 3 случая

1. кв.ур-е имеет разные корни α1 α2, D>0 тогда общее решение:

y=C1 C1, C2 прин.R

2. корни кв.ур. кратные, т.е. α1= α2=α ; D=0

y= C1, C2 прин.R

3. корни комплексно сопряженные : λ1= α-βi; λ2= α+βi;

y= C1 C1, C2 прин.R