16 Ряд Фур’є в комплексній формі

Якщо в ряді Фур’є скористатись формулами Ейлера , то ряд набуде вигляду: - комплексна форма представлення ряду, де .

17 Інтеграл Фур'є. Теорема Фур'є. Амплітудний і фазовий частотні спектри.

Нехай - функція, що задовольняє умовам Діріхлє на проміжку , і при цьому може бути вибраним довільно, і при цьому є збіжним

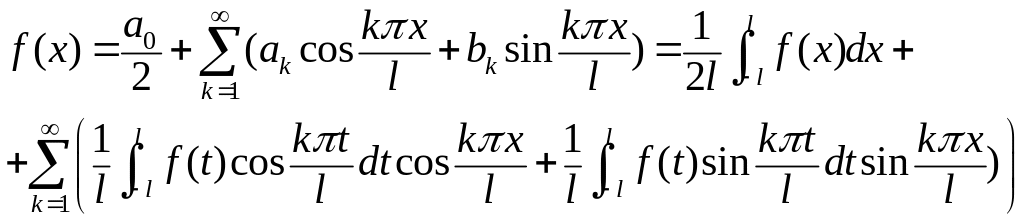
Запровадимо параметр та

при зміні і може пробігати всю додатню піввісь.

В такому випадку сума присутня у ряді Фур'є може розглядатися як інтегральна для інтеграла наступного вигляду:

Такий спосіб представлення функції називається представленням її інтегралом Фур'є.

Зауваження:

1. Аналогічно до рядів Фур'є в такому в її точках неперервності. в точках розриву.

2. визначає амплітудний спектр функції, в вираз її фазовим спектром.

3. Для такого представлення функції спектр виявляється неперервним, а не лінійчастим

4. Амплітудний спектр може розглядатись як щільність розподілу енергії по частотах коливань.

5. Інтеграл Фур'є може бути записаний у вигляді

18 Інтеграл Фур’є для парних і непарних ф-й. Синус і косинус перетворення Фур’є.

Інтеграл Фур’є має вигляд: 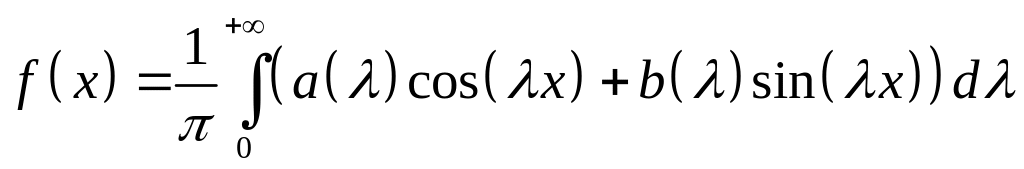. У випадку якщо ф-я є парною або непарною його можна спростити наступним чином:

• у випадку, якщо ф-я є парною , то . В результаті чого отримуємо косинус перетворення Фур’є.

• у випадку, якщо ф-я є непарною , то . В результаті чого отримуємо синус перетворення Фур’є.

19 Інтеграл Фур’є в комплексній формі.

Інтеграл Фур’є має вигляд:

Даний інтеграл можна записати в комплексній формі, в результаті отримаємо: , де .

20 Комплексні числа. Алгебраїчна, тригонометрична та показникові форма числа, дії над комплексними числами, формула муавра, корінь n степіня

_{Комплексним числом в алгебраїчній формі називається вираз вигляду , де} і дійсні числа, − уявна одиниця. При цьому:

− дійсна частина КЧ;

− уявна частина КЧ;

Комплексні числа рівні тоді, коли рівні їх дійсна і уявна частини одночасно.

Якщо на КП звичайним чином запровадити ПСК, то КЧ може бути записане у вигляді − така форма запису називається тригонометричною формою КЧ, при цьому − називається модулем КЧ, а полярний кут − аргументом КЧ.

Застосувавши формулу Ейлера до вище наведеного виразу отримаємо показникову форму КЧ − .

_{Дії з КЧ:}

• _{Спряженим до КЧ називається число}

• _{Додавання (віднімання) КЧ здійснюється по координатно.}

• _{Множення КЧ виконується за наступним правилом:} , якщо КЧ у тригонометричній формі, то множення відбувається наступним чином:

• При множенні КЧ на спряжене до нього отримуємо квадрат модуля цього числа:

• При множенні КЧ на дійсне, його дійсна та уявна частини множаться на це число.

• Ділення КЧ здійснюється за правилом: , якщо КЧ задані у тригонометричній (показниковій) формі, то ділення відбувається досить просто:

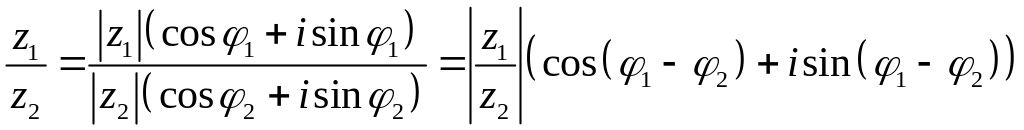
Правило множення КЧ дозволяє встановити 1-у формулу Муавра: , де натуральне.

Коренем -го степеня з КЧ називається число, яке будучи піднесеним до -го степеня стає рівним . Існує різних коренів КЧ, які задаються наступною формулою: 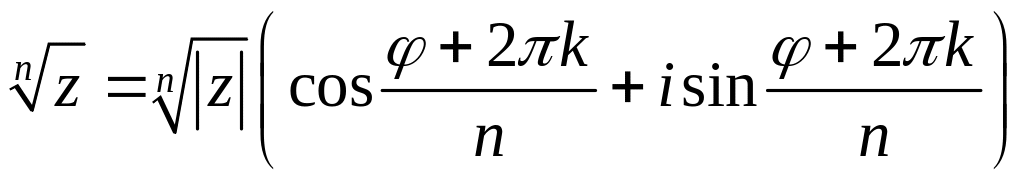, при цьому корінь -го степеня з вважається арифметичним,