14. Многочлен Ньютона с конечными разностями

В рассмотренных выше методах не делалось никаких предположений о плотности распределения узлов интерполяции. Рассмотрим случай равноотстоящих узлов интерполяции, то есть x_i - x_i-1 = const = h, i=1,n. h - называется шагом.

Введем понятие конечных разностей. Пусть некоторая функция задана таблицей. Составим разности значений функции:

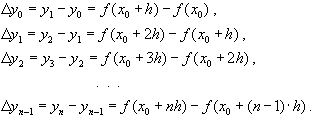
Эти разности называются разностями первого порядка. Можно составить разности второго порядка:

Аналогично составляются разности k-го порядка:

Выразим конечные разности непосредственно через значение функции:

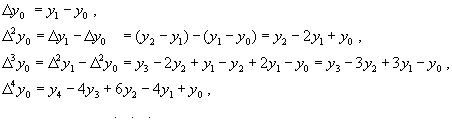
Таким образом, для любого k можно записать:

Запишем эту формулу для значений разности в узле x_i:

Используя конечные разности можно определить

Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде:

График многочлена должен проходить через заданные узлы, то есть N(x_i)=y_i(i = 0,n). Используем эти условия для нахождения коэффициентов многочлена:

Найдем отсюда коэффициенты a_i :

Таким образом для любого k-го коэффициента формула примет вид:

Подставляя эти формулы в выражение многочлена Ньютона получим его следующий вид:

Полученную формулу можно записать в упрощенном виде. Для этого введем переменную

В этом случае:

С учетом этих соотношений формулу многочлена Ньютона можно записать в виде:

Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед.

Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае t=(x-x_n)/h<0 и интерполяционный многочлен Ньютона можно получить в виде:

15. Сплайны.

И спользование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных в точках стыка двух соседних многочленов. В некоторых случаях эта особенность не играет большой роли при решении задачи интерполяции. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x₀; x_n] гладкость.

Пусть отрезок [x₀; x_n] разбит на n частей [x_i-1; x_i]. Тогда сплайном степени m S_m(x) наз. ф-ия, обладающая след. св-ми:

1. ф-ия S_m(x) непрерывна на всём отрезке от [x₀; x_m] вместе со своими производноми до некоторого порядка Р;

2. На каждом отрезке [x_i-1; x_i] сплайн совпадает с некоторым многочленом степени m. S_m(x)=P_m,i(x)

Разность теорем между степенью сплайна и наивысшей на отрезке (x₀; x_n) непрерывной производной наз. дефектом сплайна. Показанный на рисунке. Дефект сплайна = 1.

На практике наиб. распространенные кубич. сплайны с дефектом 1 или 2. На каждом отрезке такой сплайн совпад. с полиномом вида:

Значения называется наклоном сплайна в точке x_i. Т.о., отрезке (x_i-1; x_i) кубический сплайн однозначно определяется величинами

(1)

Фактически задача сводится к определению наклонов сплайна S_i-1 и S_i :

Если в т. x_i , где , нам известны не только величины , но и величины , то естественно предположить: . Получаемый в этом случае сплайн называется локальным.

Можно потребовать, чтобы кубический сплайн имел непрерывную на отрезке от x₀ до x_n 2-ю производную. Для этого наклоны Si должны быть подобраны т.о., чтобы в т. стыка x_i у соседних полиномов P_3,i(x) и P_3,i+1(x) совпадали значения 2-х производных: . Используя ф-лу (1), найдём выражения 2-х производных

Приравниваем значения 2-х производных в т. стыка, получим систему из n-1 ур. для n+1 неизвестного:

Полученная система явл. не доопределённой.

Е сли известны численные значения , то найденная система дополнилась бы 2-я ур.: для левой границы:

Если численные значения неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x₀ и x_n = 0.