Метод простой итерации.

Для того чтобы применить метод простой итерации к решению СЛАУ Aх=b преобразуем ее к виду х=Вх+с, (3). Зададим некоторое начальное приближение x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,..., x_n⁽⁰⁾). Подставив его в правую часть системы (3), находим первое приближение x₍₁₎= Bx₍₀₎+c и так далее.

Сходимость метода простой итерации.

Если норма матрица ||B||<1, существует и единственное решение системы (3) и метод сходится при произвольном начальном приближении x⁽⁰⁾.

Евклидова норма матрицы, имеет вид:

К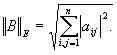 ритерий окончания итерационного процесса: ||x⁽ⁿ⁾-x^(n-1)|| < 

Метод Зейделя.

Пусть система (1) приведена к виду (2). Метод Зейделя представляет собой модификацию метода простых итераций. Идея метода состоит в том, что при вычислении на (k+1)-ом шаге х_i^k+1, используется уже найденное x_j^k+1, j=1,i.

Таким образом матрица В разбивается на две треугольные матрицы: верхнюю и нижнюю.

Расчетная формула принимает вид:

x ^k+1 =B₁ x ^k+1 + x ^k + C

или

Условия сходимости и критерий окончания итерационного процесса те же.

Метод релаксации.

Исходную систему (1) преобразуем к виду –x+Bx+c=.

Зададим начальное приближение и подставим в полученную систему. Получаем невязки (отклонения)

).

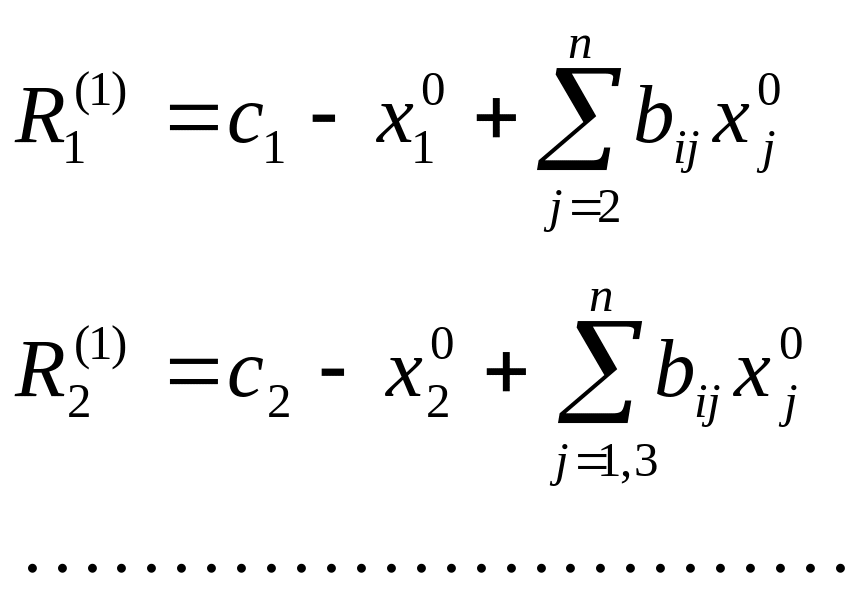
Если одной из неизвестных x_s⁽⁰⁾ задать приращение x_s⁽⁰⁾, то соответствующая невязка уменьшится на эту величину, а все остальные невязки R_i⁽⁰⁾(iS) увеличатся на величину b_is x_s⁽⁰⁾.то есть, чтобы обратить очередную невязку R_s⁽¹⁾ в нуль, необходимо величине x_s⁽⁰⁾ дать приращение  x_s⁽⁰⁾= R_s⁽⁰⁾ и получим R_s⁽¹⁾=0 и R_i⁽¹⁾= R_i⁽⁰⁾ + b_is x_s⁽⁰⁾.

Таким образом, идея метода состоит в том, чтобы на каждом шаге обращать в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.

Метод прогонки.

Метод предназначен для решения задач вида:

i=1, n-1

Метод состоит из 2-х частей: прямого и обратного хода. На прямом ходе рассчитываются дополнительные коэффициенты, используемые для вычисления неизвестных x:

1. i=0,

2. i=1, n-1,

3. i=n,

Обратный ход: x_n=b_n; i=0, n-1 x_i=α_ix_i+1+β_i

9. Вычисление собственных чисел матрицы.

В процессе конструирования и анализа больших технич. систем инженеру очень часто приходится сталкиваться с задачей нахожд. собств. чисел и собственных векторов исследуемой системы, кот. характеризуют её внутренние св-ва. Математически задача нахождения собственного числа выглядит след. образом: Пусть задана квадратная матрица Аm,m. Обозначаем скалярное произведение 2-х векторов:

- норма.

Число  явл. собств. числом матрицы А, если найдётся ненулевой вектор Х, для кот. вып. равенство (1) Ах = х. В этом случае вектор Х наз. собственным вектором матрицы А. Запишем (1) в др. виде: (А-Е)х=0 (2). Е – единичная матрица. Эта система будет им. ненулевое решение тогда, когда определитель матрицы det (A-E)=0 (3). Раскрывая ур. (3), мы получаем характеристическое ур. вида: . Известно, что алгебраическое ур. степени m им. m корней в области комплексных чисел, т.е люб. матрица А порядка m им. ровно m собственных значений, комплексно сопряжённые. Во многих дисциплинах сущ. задачи, связывающие с выч. всех собств. чисел. В этом случае задача наз. полной проблемой собственных значений. Однако, гораздо чаще в задачах треб. определить одно собственное значение или некоторую их часть. Такие задачи наз. частичной проблемой собственных значений. В плане постановки такой задачи существующий интерес представляет нахождение собственного числа, наиболее близкого расположенного к заданному, или нахождение наибольшего или наименьшего собственного числа. Характеристическое ур. можно решать любым численным методом с последующим понимание порядка ур. после нахождения одного из корней. Пример:

₁=1; делим на -1: -²+8-13=0 → ₂=4±

Описанный приём для реш. характерного ур. относят к прямым методам реш. проблем собственных значений. Их применению может воспрепятствовать высокий порядок m, когда корни характеристического ур. становятся чувствительны к погрешности и м.б потеряна достоверная инф. об m величене. Рассмотрим один из самых простых методов реш. задачи о собственных числах – степенной метод без сдвигов. Пусть требуется определить max по модулю собственное значение ₁ матрицы А. ₁ д.б вещественным. Возмём произвольный вектор х⁰ и построим из него последовательность векторов и Итерационный процесс:

Теорема: Пусть задана матрица А достаточно простой структуры, для кот. |₁|>|₂|≥|₃|≥…≥|_m|. Предположим что разложение х⁽⁰⁾ по базису собственных векторов х⁰=С₁е₁+ С₂е₂+…+ С_mе_m происходит с С₁≠0. Тогда |^k₁| → |₁|^k→∞и справедлива следующая оценка погрешности: Исходя из формулы (4), можно записать, что х^(к)=А^к х⁽⁰⁾. Допускается следующее усовершенствование метода: y^(к)=Ах^(k-1), ^(к)=( y^(к), y^(к-1)), Для того. чтобы схема была работоспособной, нужно, чтобы ||x⁽⁰⁾||=1. Подобный подход позволяет избежать возникших в результате вычислений проблем с переполнением или потерей порядка. Одним из недостатков степенного метода без сдвигов явл. его медленная сходимость применительно ко многим прикладным задачам.