21. Общая постановка задачи Коши.

При рассмотрении технических систем и технологических процессов инженеру часто приходится сталкиваться с их характеристиками, которые непрерывным образом меняются во времени t. Такие явления подчиняются физическим законам, описываемым дифференциальными уравнениями. Одной из основных математических задач, решаемых для таких уравнений, является задача Коши. Обычно, к ней приходят, когда известно начальное состояние системы в момент времени t₀ и требуется предсказать ее поведение в момент времени t > t₀.

Рассмотрим задачу Коши для дифференциального уравнения первого порядка: (1)

Решением уравнения (1) является дифференцируемая функция y(t), которая при подстановке в уравнение (1) превращается в тождество. График y(t) называется интегральной кривой рис. (1), а процесс решения называется интегрированием.

Заметим, что уравнение (1) задает в каждой точке (t, y) тангенс угла наклона касательной к графику решения, проходящего через эту точку.

Если в каждой точке (t, y) задать с помощью некоторого вектора направление касательной, определенной значением f (t, y), то получится поле направлений.

Геометрическая задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Для того чтобы выделить из семейства решений дифференциального уравнения (1) конкретное решение, задают начальное условие: y(t₀)=y₀

22. Метод Эйлера.

Воспользуемся формулой Тейлора:

(2)

R_(p+1)(t,h) - остаточный член. Если его отбросить, то получим приближенное равенство:

Если значение решения у в т. t известно, то в силу равенства (1) можно считать известными y’(t). Для нахождения производных продифференцируем Ур. (1) по t. Получим:

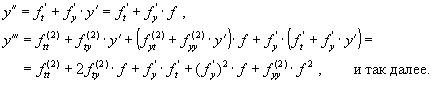
В ыражения усложняются по мере роста порядка K.

Использование приближенной формулы (3) приводит к формуле:

Метод Эйлера является первым и простейшим методом решения задачи Коши. Его можно получить, если в приближенном равенстве (4) положить p = 1, то есть оставить два первых слагаемых.Получим:

Геометрическая интерпретация одного шага метода Эйлера заключается в аппроксимации решения на отрезке [tn, tn+1] касательной y=yn+y'(tn) (t-tn), проведенной в точке (tn,yn) к интегральной кривой, проходящей через эту точку. Таким образом, после выполнения N шагов неизвестная интегральная кривая заменяется ломаной линией, для которой угловой коэффициент k_n очередного n - го звена равен значению f (t_n, y_n). (рис. 3) Погрешность аппроксимации в этом случае имеет вид:

23. Метод Рунге - Кутта.

Является наиболее популярным из одношаговых методов. Пусть y (t) - решение дифференциального уравнения y' = f (t,y), удовлетворяющее условию y (t_n) = y_n. Из формулы Ньютона - Лейбница

следует: (6)

Если интеграл в формуле (6) можно было вычислить точно, то получилось бы простое выражение. Однако, в действительности это невозможно, поэтому будем строить приближенную формулу, заменив интеграл квадратурной суммой. Введем на отрезке [t_n,t_n+1] m вспомогательных узлов

где

Заменяя, входящий в равенство (6) интеграл квадратурной суммой с узлами t_n⁽¹⁾, ... ,t_n^(m), получим приближенное равенство:

(7)

Однако воспользоваться равенством (7) нельзя, т.к. значения y в т. неизвестны. Чтобы найти их запишем:

(8)

Заменяя в этом равенстве для каждого i входящий в него интеграл соответствующей квадратурной формулой с узлами t_n⁽¹⁾, t_n ⁽²⁾, ... , t_n^(i-1), получим приближенные равенства:

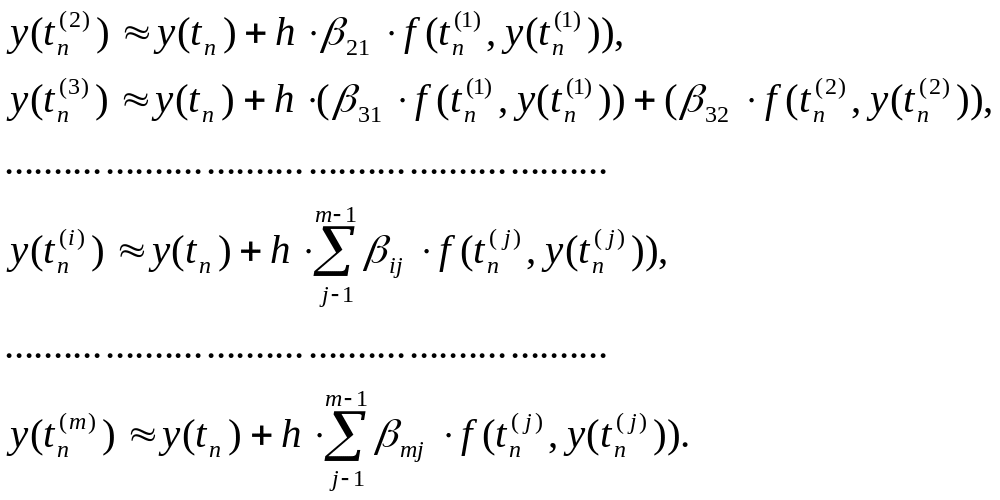
позволяющие последовательно вычислить приближения k y(t_n⁽²⁾), ..., y(t_n^(m)). Обозначим через y_n⁽ⁱ⁾ вспомогательные величины, являющиеся приближениями k y(t_n⁽ⁱ⁾). Пусть k_n⁽ⁱ⁾ = f (t_n⁽ⁱ⁾, y_n⁽ⁱ⁾) - приближение к значению углового коэффициента k в точке t_n⁽ⁱ⁾. В этом случае расчетные формулы примут вид:

Если выбросить вспомогательные величины y_n⁽ⁱ⁾, то те же формулы можно записать в виде:

Полученный метод носит название m - этапного метода Рунге - Кутта.

Выбор конкретных значений параметров осущ. исходя из различных соображений, одним из кот. м. б. желание сделать порядок аппроксимации максимально возможным.