1. Основные понятия вычислительной математики.

П рименение ВТ базируется на описании процессов реального мира мат. модели, которая представляет собой совокупность обычных интегральных и дифференциальных уравнений. Всякая математическая модель представляет собой математическое преобразование вида «черный ящик», где x(x₁..x_n) вектор входных параметров объектов, y(y₁..y_m) вектор управлений воздействий на объект, U(U₁..U_k) совокупность выходных параметров объектов и F - оператор преобразования.

Для решения математических задач применяется 3 группы методов: аналитические, графические, численные.

Графические методы предполагают искать решение с помощью геометрических построений.

Аналитические методы предполагают искать решение задачи в виде формулы.

Численные методы являются основными методами в САПР. В их основе лежит процедура сведения решения задачи к конечному числу арифметических действий над числами, и получить результат в виде численных значений.

Основные требования и показатели численных методов является устойчивость, точность, сходимость, эффективность (скорость сходимости).

Алгоритм считается устойчивым, если он обеспечивает нахождение существующего и единственного решения при различных исходных данных.

С ходимость является основным критерием оценки алгоритма. Алгоритм сходится, если итерационная последовательность приближений x¹,x²,...,x^k x^* , k   , т. е.

Скорость сходимости выражается в количестве шагов, которое метод затрачивает для поиска решения.

Алгоритм обладает линейной скоростью сходимости, если a<q<b, |x^k-1-x*|≤q|x^k-x*|.

Алгоритм обладает сверхлинейной скоростью сходимости, если выполняется условие |x^k+1-x^*|q_k |x^k-x^*| , q 0 , k  .

Алгоритм обладает квадратичной скоростью сходимости, если |x^k+1-x^*|q|x^k-x^*|².

2. Решение нелинейного уравнения методом простых итераций. Понятие сжимающего отображения. Теорема о сходимости. Геометрическая интерпретация. Метод простой итераций.

Пусть требуется решить уравнения вида f(x)=0 (1), где f(x) - непрерывная функция.

Чтобы решить уравнения (1) его необходимо преобразовать к виду x=(x) (2). Зададим начальное приближение x₀ и подставим его в правую часть уравнения (2), получим значение х₁. Повторяя этот процесс можно получить итерационную последовательность приближения к корню уравнения (1). В общем виде описанную формулой x^k+1=(x^k), k 0.

Если существует придел x*=limx^k, то исходя из непрерывности функции (x) можно записать x*=(x*) – корень уравнения (1).

Условие сходимости метода. Понятие сжимающего отображения.

Т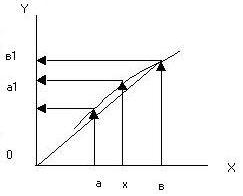 еорема: Пусть в некоторой δ - окрестности корня х^* функция φ(х) дифференцируема и удовлетворяет неравенству |φ'(x)|≤ q, 0 < q < 1. Тогда независимо от выбора начального приближения х₀ из указанной δ - окрестности корня итерационная последовательность не выходит из этой окрестности и справедлива следующая оценка сходимости: |x^k-x^*|<q|x₀-x^k| что говорит о линейной скорости сходимости.

Решить вопрос о сходимости метода можно с помощью понятия сжимающее отображение.

Доказательство: Возьмем непрерывную функцию φ(х) заданную на некотором отрезке [a;b]. Каждой точке x из отрезка [a;b] соответствует некоторое значение y = φ(х) на оси ординат. Т.е. функция отрезка a;b задает отображение на оси ординат. Чтобы сравнить образ отрезка с ним самим отобразим отобразить точки на оси 0y через симметрично относительно прямой y=x. Если образ отрезка a;b является частью a;b , то (x) отображает a;b в себя. Будем продолжать этот процесс бесконечно и полечим последовательность отрезков. Если после каждого отображения отрезок уменьшается в М>1 раз, то отображение называется сжимающим и можно записать следующее

|φ(a)-φ(b)|≤q|a-b|, q=1/M.