
- •Модуль 1. Числовые и линейные неравенства
- •Практическая часть
- •Устные упражнения
- •Практическая часть
- •Устные упражнения
- •Входная информация
- •Практическая часть
- •«Линейное неравенство с одной переменной»
- •Практическая часть
- •Устные упражнения
- •Линейных неравенств
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •10 Класс.
- •Рубрика «Ваш помощник»
- •Сводящихся к линейным неравенствам
- •Входная информация
- •1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное исходному;
- •2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное исходному;
- •3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное исходному.
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Практическая часть
- •Устные упражнения
- •Рубрика “Ваш помошник”
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Практическая часть
- •5) Найденные множества решений объединяют и записывают ответ.
- •Практическая часть
- •Входная информация
- •Практическая часть
- •Рубрика “Ваш помощник”
- •Входная информация.
- •Рубрика “Ваш помощник”
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Нематематики о математике
- •Практическая часть
- •Содержащих квадратные корни
- •Входная информация
- •Практическая часть
- •Входная информация
- •Входная информация
- •Математическая мозаика Из истории введения действия извлечения квадратного корня из числа
- •Интересные задачи
- •Софизмы
- •А. Эйнштейн
- •Модуль 4.
- •Квадратные уравнения.
- •Уравнения, сводящиеся к квадратным уравнениям
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Рубрика «Ваш помощник»
- •На линейные множители
- •Входная информация
- •Упражнения
- •Рубрика «Ваш помощник»
- •Уэ 5. Теорема Виета
- •Входная информация
- •Рубрика «Ваш помщник»
- •Входная информация
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •С целыми коэффициентами
- •Практическая часть
- •Учимся доказывать теоремы
- •Содержание
Рубрика «Ваш помощник»
К заданию 1. Ответы к устным упражнениям:
а)
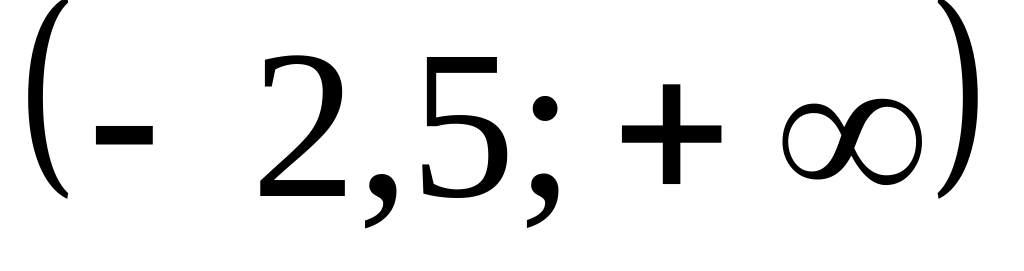 ;
б)
;
б)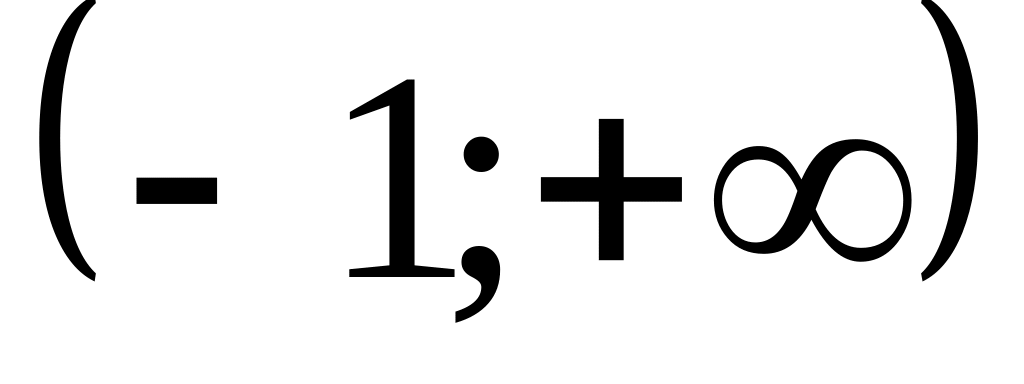 ;
в)
;
в)
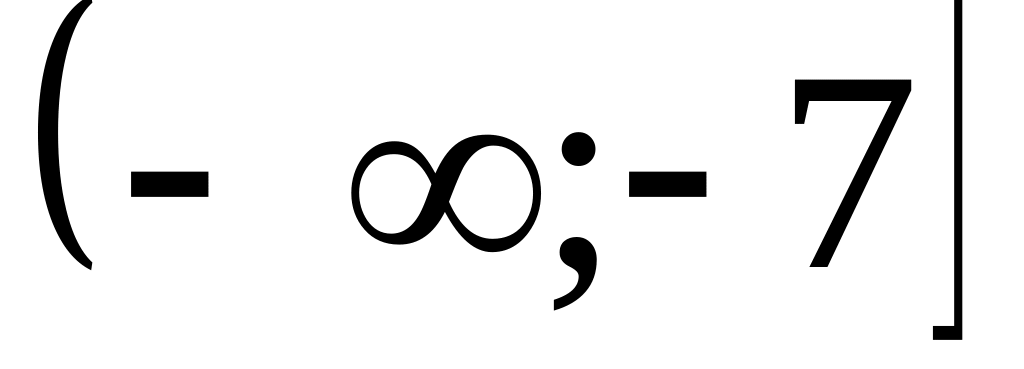 .
.а) ; б)
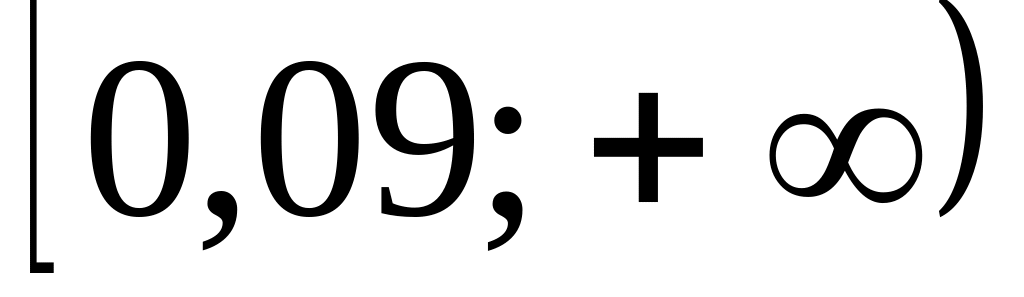 ;
в)
;
в)
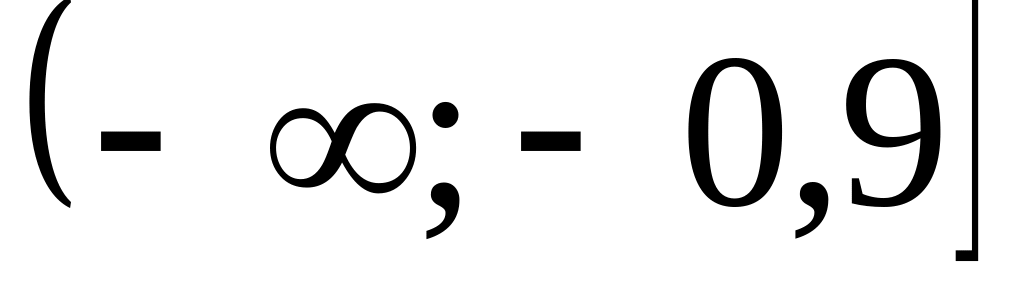 ;
г)
;
г)
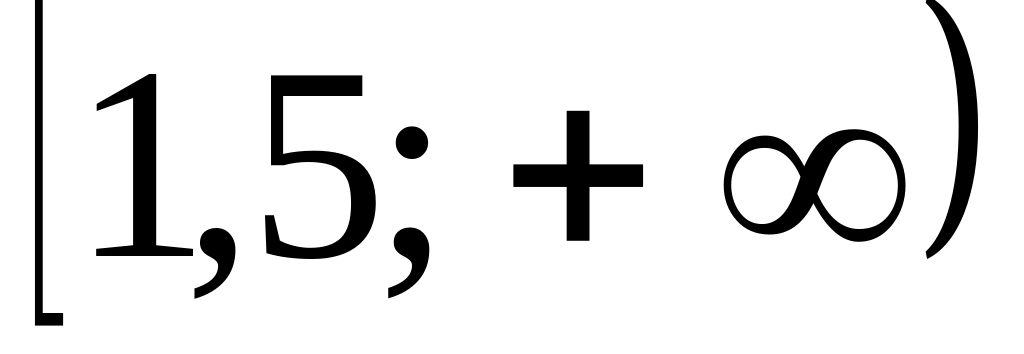 .
.а)
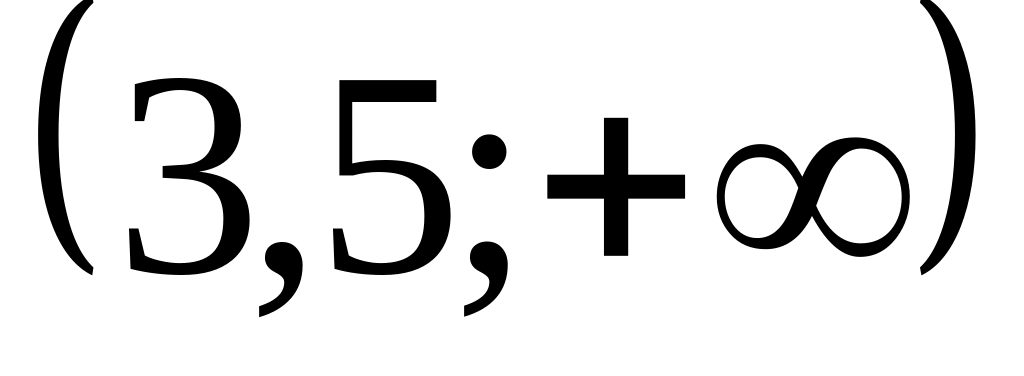 ;
б)
;
б)
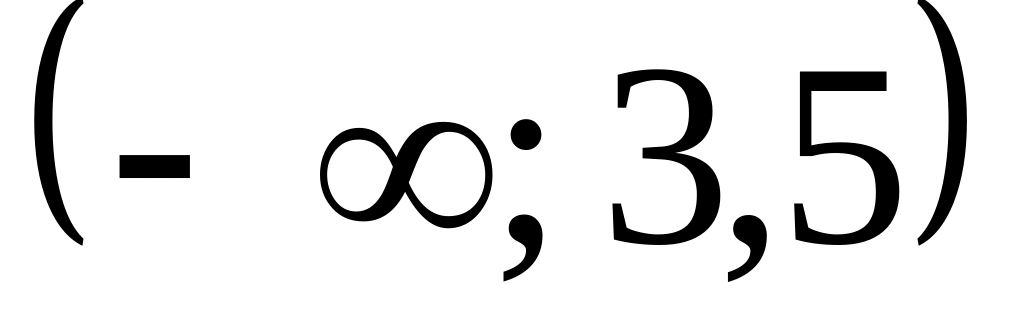 .
.
К
заданию 2. а) нет
решений; б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
К
заданию 3. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
.
;
г)
.
К
заданию 4.а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
К
заданию 5.а)
![]() ;
б)
;
б)
![]() .
.
К
заданию 6. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
е)
;
д)
;
е)
![]() .
.
К
заданию 7.а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
К
заданию 9. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
К заданию 10.а) 1; 2; 3; 4.
К заданию 11. 6.
К заданию 12. Длина другой стороны больше нуля, но меньше шести.
К
заданию 15.
![]() .
.
УЭ-7. Системы и совокупности линейных неравенств
Ваша цель: знать определение решения системы (совокупности) неравенств и знаки, применяемые для их обозначения; уметь решать системы и совокупности простейших неравенств; уметь решать двойные неравенства.
Входная информация
Понятие системы неравенств. Несколько неравенств с одной переменной образуют систему, если нужно найти множество всех общих решений заданных неравенств.
Неравенства, образующие систему, объединяются фигурной скобкой, например:
Определение. Решением системы неравенств с одной переменной называется значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.
Множество решений системы есть пересечение множеств решений, входящих в нее неравенств.
Учимся решать системы неравенств. Рассмотрим примеры решения систем неравенств.
Пример 1. Решим систему неравенств
Решение. Преобразовав каждое неравенство, входящее в систему, получим:
Множество решений первого неравенства (–¥; 7), второго – (3; +¥). Очевидно, что множеством решений системы является пересечение этих двух множеств. Это пересечение можно найти с помощью координатной прямой .
Системе неравенств удовлетворяет любое число из интервала (3; 7).
Ответ: (3; 7).
Пример 2. Решим двойное неравенство
–1 < < 1.
Решение. Двойное неравенство можно рассматривать как систему неравенств:
Решим ее:
Множество решений системы, а следовательно, и двойного неравенства – числовой интервал (– 1; 2) (рис.2 ).
Решение двойного неравенства можно найти по-другому:
–1 < < 1.
Умножив неравенство почленно на 3, получим:
–3 < 2x – 1 < 3.
Прибавляя к каждой из частей неравенства 1, получаем равносильное исходному неравенство –2 < 2х < 4. Разделив полученное неравенство почленно на 2, приходим к неравенству
–1 < x < 2.
Ответ: (–1; 2).
Понятие совокупности неравенств. Несколько неравенств с одной переменной образуют совокупность, если нужно найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств.
Для обозначения совокупности неравенств используется прямая скобка [. Так, запись означает, что неравенства образуют совокупность. Иногда неравенства, образующие совокупность, записывают в строчку и отделяют друг от друга логической связкой «или». Например,
2х – 3 < 1 или 3х + 1 > 10.
Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.
Множество решений совокупности есть объединение множеств решений входящих в нее неравенств.
Учимся решать совокупности неравенств. Определим, что значит решить совокупность систем неравенств.
Решить совокупность систем неравенств с переменной х – значит найти все такие значения х, которые удовлетворяют по крайней мере одной из заданных систем.
Другими словами, решением совокупности систем является объединение решений этих систем.
Рассмотрим примеры решения совокупностей неравенств.
Пример 4. Решим совокупность неравенств
Получаем:
Множество решений неравенства х > 9 – числовой промежуток (9; +¥), неравенства х > 4 – числовой промежуток (4; +¥). Пользуясь координатной прямой, находим, что объединением этих множеств является числовой промежуток (4; ¥) (рис. 3).
Ответ: (4; +¥).
