3 Нелинейное программирование
3.1 Построение одзп, выбор начальной точки поиска
Целевая функция имеет вид:
Построим ОДЗП:
Рисунок 3.1 - ОДЗП
Внутри области допустимых значений выбираем точку x0, которая в дальнейшем будет являться начальной в процессе поиска экстремума:
x0=(3;1).
3.2 Нахождение экстремального значения функции f(X) без учета ограничений на переменные
3.2.1 Метод наискорейшего спуска
В методе наискорейшего спуска (подъема) очередная точка при поиске максимума функции вычисляется по формуле:
(3.1)
где “+” для задачи на максимум, а “-” – на минимум.
Найдем
градиент
:
;
(3.2)
.
На
первом шаге движение осуществляется
из точки
в направлении, обратном вектору
в новую точку
:
Величина шага
на любом шаге выбирается из условия
обеспечения экстремума функции в
рассматриваемом направлении. Подставляя
координаты точки
в функцию
,
получим:
;
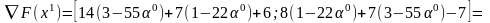
Из условия:
;
найдем
:
;
;
;
В результате после первого шага координаты очередной точки получаются равными:
Вычисляем
:
.
На втором шаге движение осуществляется
в направлении, обратном вектору
с увеличением шага
:
;
;
;
;
;
В результате после второго шага координаты очередной точки получаются равными:
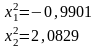
Вычисляем
:
.
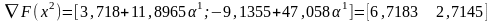На третьем шаге движение осуществляется
в направлении, обратном вектору
с увеличением шага
:
;
;
;
;
;
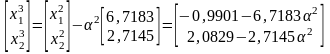
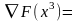
В результате после третьего шага координаты очередной точки получаются равными:
Вычисляем
:
.
На третей итерации закончим
вычисления, значение функции цели:
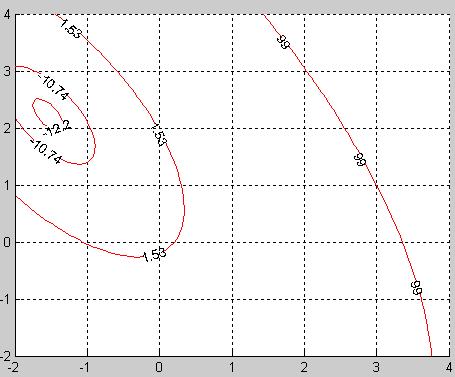
Рисунок 3.2 – Графическая интерпретация метода наискорейшего спуска
3.2.2 Метод Ньютона-Рафсона
Данный метод дает решение задачи за 1 шаг. Очередная точка поиска вычисляется в соответствии с выражением:
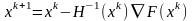(3.3)
где
– матрица Гессе функции
;
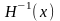– обратная по отношению к
матрица.
Градиент F(x):
;
.
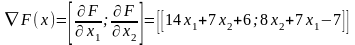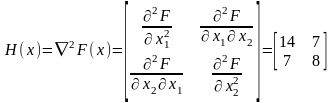(3.4)
где det H – определитель матрицы H; AdjH – присоединенная к H матрица (транспонированная матрица алгебраических дополнений).
Найдем определитель матрицы Гессе:
Найдем транспонированную матрицу алгебраических дополнений AdjH:
Теперь найдем матрицу обратную по
отношению к
- матрицу
:
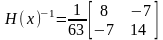
тогда:
Следовательно,
в точке
функция
F(x)
достигает максимального значения.
3.3 Нахождение экстремального значения функции f(X) с учетом системы ограничений задачи
23.3.1 Метод допустимых направлений Зойтендейка
Координаты следующей точки:
.
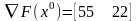Тогда координаты очередной точки:
Определяем интервал допустимых значений для 0, при котором точка x1 будет принадлежать ОДЗП. Для этого подставим координаты точки x1 в ограничения задачи:
=> 
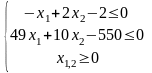Тогда:
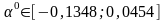
Находим величину ,которая обеспечит минимум функции F(x). Воспользуемся уже найденным =0,199 (метод наискорейшего спуска, стр. 29), но т.к. оно не входит в найденный интервал, то =0,0454. Координаты точки и значение градиента функции в этой точке :
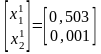
На следующем шаге двигаемся в направлении
и
попадаем в очередную точку.
Координаты очередной точки:
Определяем интервал допустимых значений для 1, при котором точка x2 будет принадлежать ОДЗП. Для этого подставим координаты точки x2 в ограничения задачи:
Находим величину ,которая обеспечит минимум функции F(x) из условия
Полученное
значение
не входит в найденный ранее интервал,
поэтому примем
.
Тогда:
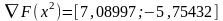
Движение вдоль выводит за вершины ОДЗП, следовательно следующую точку ищем в соответствии с выражением:
(3.5)
где
- новое направление, которое составляет
минимальный острый угол с вектором
градиента и направлено либо внутрь,
либо по границе ОДЗП. При этом очередная
точка должна принадлежать ОДЗП.
Найдем направление
очередного шага: т.к. x2
и точка экстремума лежат на оси [0;X2],
то
При движении из точки x2 в точку x3 следует двигаться по граничной прямой в направлении , как показано на рис. 3.3.
Координаты точки x3 определяются выражением:
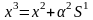
или
Находим
интервал изменения
,
при котором
принадлежит ОДЗП:
Найдем такое 2, которое обеспечит минимум F(x) в направлении
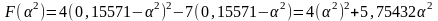
тогда
Вычисляются составляющие вектора градиента в точке x3:
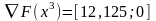
Направление вектора
перпендикулярно направлению
,
следовательно, найденная точка
обеспечивает минимум функции F(x)
с учетом ограничений на переменные:
Рисунок 3.3 - Графическая интерпретация метода допустимых направлений Зойтендейка