Министерство образования Республики Беларусь

Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники»

Факультет информационных технологий и управления

Кафедра систем управления

Пояснительная записка

к курсовому проекту по курсу:

«Математические основы теории систем»

Выполнил: Руководитель:

студент гр. 922402 Павлова А.В.

Дубовик А.И.

Минск 2011

Содержание

Факультет информационных технологий и управления 1

Кафедра систем управления 1

Пояснительная записка 1

«Математические основы теории систем» 1

1 Математическое описание линейных систем 3

1.1 Дифференциальное уравнение системы. Характеристическое уравнение и его корни 3

1.2 Разложение передаточной функции на сумму простых слагаемых. Вычисление импульсной переходной характеристики ω(t) с помощью обратного преобразования Лапласа и переходной характеристики h(t) 4

1.3 Построение ЛАЧХ и ЛФЧХ 6

1.4 Уравнение состояния в нормальной форме,схема моделирования 7

1.5 Уравнение состояния в канонической форме, 9

схема моделирования 9

1.6 Решение уравнения состояния в нормальной и канонической формах 13

1.7 Проверка: одинаково ли значение коэффициента усиления по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики 16

2 Линейное программирование 18

2.1 Математическая модель задачи. Нахождение оптимального плана х* и экстремального значения функции 18

2.2 Построение и решение задачи, двойственной к исходной. Сравнение решения прямой и двойственной задач 20

2.3 Получение целочисленного решения путем введения дополнительных ограничений по методу Гомори 23

3.1 Построение ОДЗП, выбор начальной точки поиска 25

3.2 Нахождение экстремального значения функции F(x) без учета ограничений на переменные 26

3.2.1 Метод наискорейшего спуска 26

3.2.2 Метод Ньютона-Рафсона 29

3.3 Нахождение экстремального значения функции F(x) с учетом системы ограничений задачи 30

23.3.1 Метод допустимых направлений Зойтендейка 30

3.3.2 Метод линейных комбинаций 34

3.3.3 Условия теоремы Куна-Таккера 38

4 Тексты программ в среде MATLAB 41

4.1 Математическое описание линейных систем 41

4.2 Линейное программирование 45

4.3 Нелинейное программирование 46

1 Математическое описание линейных систем

1.1 Дифференциальное уравнение системы. Характеристическое уравнение и его корни

Передаточная функция системы имеет вид:

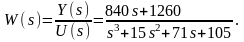(1.1)

_{Передаточная функция системы W(s) – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных условиях.}

_{Чтобы перейти от передаточной функции к дифференциальному уравнению системы, нужно перейти из области изображений по Лапласу во временную область. Из (1.1) следует:}

_{Для перехода во временную область воспользуемся формальными правилами:}

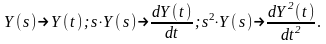
Тогда дифференциальное уравнение, соответствующее передаточной функции, имеет вид:

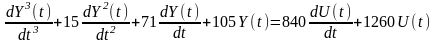(1.2)

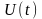где - выходной сигнал, - входной сигнал.

Характеристическое уравнение системы определяется знаменателем передаточной функции:

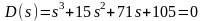
Корни характеристического уравнения имеют вид:

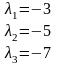
Передаточная функция системы в форме нулей и полюсов (zpk форме) имеет вид:

1.2 Разложение передаточной функции на сумму простых слагаемых. Вычисление импульсной переходной характеристики ω(t) с помощью обратного преобразования Лапласа и переходной характеристики h(t)

Получим разложение передаточной функции на сумму простых слагаемых:

Найдём a, b, c.

.

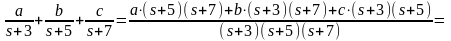
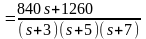Следовательно,

_{Получим систему уравнений:}

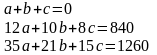
Решая эту систему, получим корни:

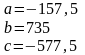
Передаточная функция:

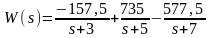
Импульсная переходная характеристика w(t) – это процесс изменения сигнала на выходе при подаче на вход δ-функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.

В соответствии с таблицами соответствия 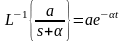, тогда:

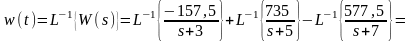
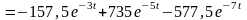
Переходная характеристика h(t) – это процесс изменения сигнала на выходе при подаче на вход единичного ступенчатого воздействия. Ее можно вычислить следующим образом:

,

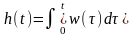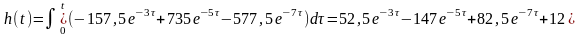
таким образом аналитическая форма переходной характеристики имеет вид:

.

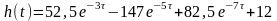Выполним проверку:

- верно;

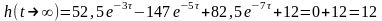- верно.

1.3 Построение лачх и лфчх

При определении частотных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.

Преобразуем передаточную функцию к следующему виду:

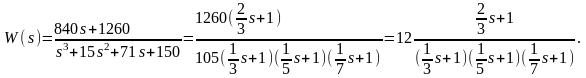
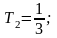
Теперь она представляет собой произведение трех апериодических и одного форсирующего звена с постоянными времени ; 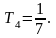Коэффициент усиления К=12. Сопрягающие частоты звеньев равны

; ; ; .

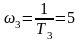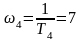ЛАЧХ приведена на рис. 1.1, а.

Рисунок 1.1 – Асимптотические ЛАЧХ (а) и ЛФЧХ (б)

Фазочастотная характеристика (рис. 1.1, б) построена в соответствии с выражением

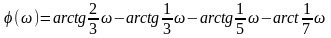
1.4 Уравнение состояния в нормальной форме,схема моделирования

Кроме входных и выходных переменных при описании систем выделяют переменные х, связанные с внутренней структурой устройства,- переменные состояния. Тогда систему можно описать с помощью уравнений состояния.

Нормальная форма уравнения состояния имеет вид:

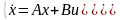(1.3)

где А – матрица Фробениуса.

Матрица Фробениуса – это квадратная матрица, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы; элементы нижней строки - это коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком, все остальные элементы – нулевые.

Дифференциальное уравнение системы имеет вид:

,

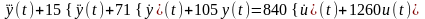
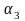
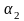
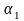
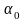
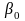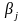где и - коэффициенты уравнения.

Для систем с одним входом и одним выходом D – одноэлементная матрица, В – вектор-столбец, состоящий из 3 элементов, которые определяются следующим образом:

;

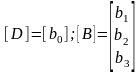
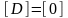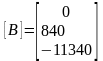
Матрица С – вектор-строка, состоящая из 3 элементов, первый элемент единица, остальные нули:

.

Подставим рассчитанные матрицы в систему (1.3), получим:

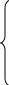
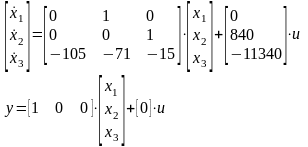
О т матричной форме перейдем к скалярной:

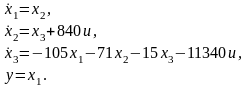
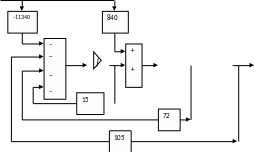
Схема модели приведена на рис.1.2:

U

∫

∫

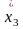
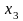
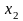
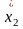
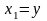
Рисунок 1.2 – Схема модели, соответствующая уравнениям состояния в нормальной форме