1.5 Уравнение состояния в канонической форме,

схема моделирования

Запишем уравнения состояния в канонической форме. Чтобы перейти к канонической форме, введем новую переменную q, которая связана с переменной состояния x следующим образом: .

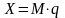М – модальная матрица, которая имеет вид:

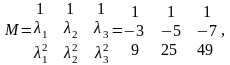
где 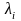- характеристические числа матрицы Фробениуса А. Модальная матрица имеет такой вид, так как матрица А имеет форму Фробениуса и все корни характеристического уравнения различны.

При подстановке q вместо х в нормальную форму уравнений состояния (1.3) получим уравнения состояния системы в канонической форме:

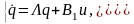(1.4)

Здесь 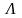- диагональная матрица:

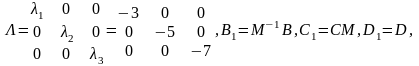
где 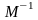- матрица, обратная модальной, определяемая выражением:

.

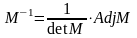Здесь 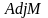-матрица, присоединенная к М, т.е. транспонированная матрица алгебраических дополнений.

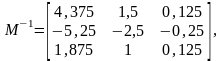
тогда

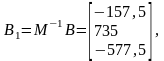
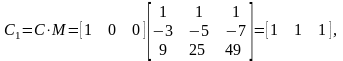
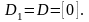
Подставим найденные значения в (1.4), получим:

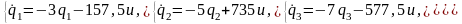
Схема модели, соответствующая полученной системе, приведена на рис.1.3. Для нее характерно параллельное соединение интеграторов, выходы которых определяются переменными состояния .

∫

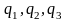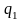
5

∫

U

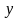
-577,5

∫

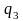
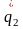
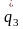
74

Рисунок 1.3 – Схема модели, соответствующая уравнениям состояния в канонической форме

Получим уравнения состояния в нормальной форме, с помощью Matlab.

ss(W) – команда, выводящая матрицы A, B, C, D

Получим:

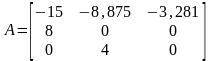
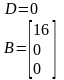
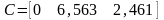
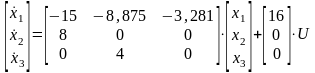
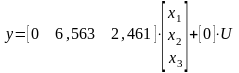
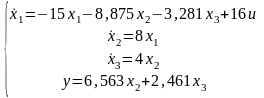
u

Рисунок 1.4 – Схема модели, соответствующая уравнениям состояния в нормальной форме

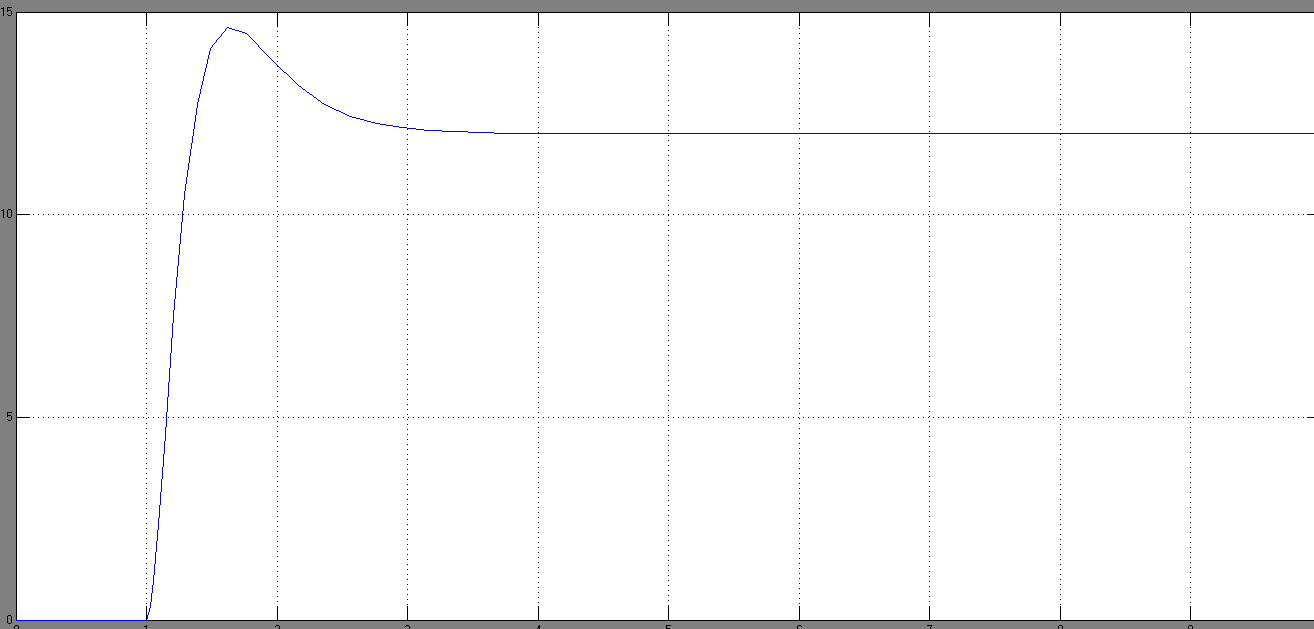
Рисунок 1.5 – Переходная характеристика

1.6 Решение уравнения состояния в нормальной и канонической формах

Найдем решение y(t) для системы уравнений в нормальной форме, если начальные условия имеют вид y(0)=1,5; . Сигнал u(t)=15∙1(t). переходя к начальным условиям для х, в соответствии с принятыми ранее обозначениями, получим:

Решение уравнения состояния 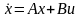складывается из двух составляющих x(t)=x₁(t)+ x₂(t) – свободной и вынужденной.

Свободная составляющая – это общее решение дифференциального уравнения системы с нулевой правой частью. Оно не зависит от внешнего воздействия и характеризует естественное поведения системы.

Вынужденная составляющая – это частное решение дифференциального уравнения с ненулевой правой частью. Оно зависит от сигнала u(t) и характеризует поведения системы под его воздействием.

Решение уравнения состояния имеет вид:

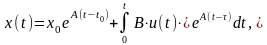
где е^At – фундаментальная матрица или матрица перехода.

Она вычисляется по следующей формуле:

е^At= γ₀E+ γ₁A+ γ₂A²,

где γ₀, γ₁, γ₂ – неизвестные коэффициенты.

Вычислить их можно, решая матричное уравнение:

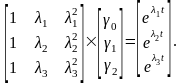
Для рассматриваемого примера:

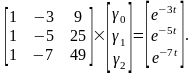
Перемножая матрицы, получаем систему уравнений следующего вида:

γ₀ -3 γ₁+9γ₂= е^-3t,

γ₀ -5γ₁+25γ₂= е^-5t,

γ₀ -7γ₁+49γ₂= е^-7t.

Решение данной системы уравнений имеет вид:

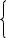γ₀=4,375e^{-3 t} – 5,25e^{-5 t}+1,875e^{-7 t},

γ₁=1,5e^{-3 t} - 2,5 e^{-5 t}+e^{-7 t},

γ₂=0,125e^{-3 t}-0,25e^{-5 t}+0,125e^{-7 t}.

=>

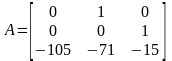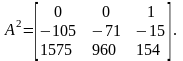
Итак,

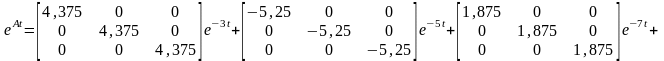
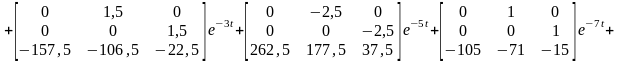
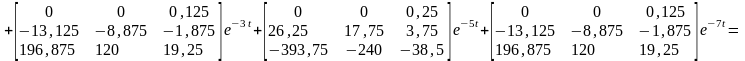
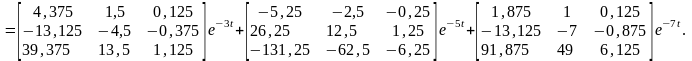
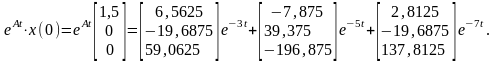
Определим вынужденную составляющую при входном сигнале u(t)=15∙1(t). Сигнал на выходе при поступлении на вход 1(t) уже вычислен – это переходная характеристика системы (1.1). Чтобы получить вынужденную составляющую сигнала в нашем случае, умножим переходную характеристику на 15.

Таким образом, сигнал на выходе системы будет следующим:

y(t)=6,5625e^-3t –7,875e^{-5 t}+2,8125e^-7t+15(52,5e^-3t – 147e^{-5 t}+82,5e^-7t+12)=

=794,0625e^-3t – 2212,875e^{-5 t}+1240,3125e^-7t +180.

_{Выполним проверку:}

_{y(0)=794,0625-2212,875+1240,3125+180=1,5 - верно;}

_{y(∞)=180 - верно.}

Найдем решение уравнений состояния, представленных в канонической форме (1.4). Каждое из дифференциальных уравнений первого порядка 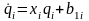зависит только от одной переменной, и его решение в общем виду имеет вид:

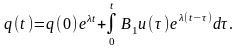
Определим начальные условия q(0) для вектора q(t).

Так как 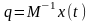, то

Найдем выражения для 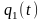, и :

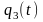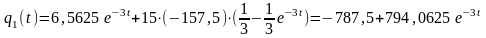
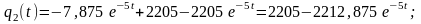
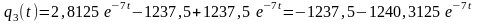
В результате получим:

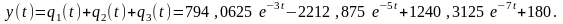
_{Выполним проверку:}

_{y(0)=794,0625-2212,875+1240,3125+180=1,5 - верно;}

_{y(∞)=180 - верно.}

_{Решения нормальных и канонических уравнений состояния совпадают.}

1.7 Проверка: одинаково ли значение коэффициента усиления по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики

Проверим значение коэффициента усиления по:

• передаточной функции:

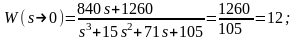
• переходной характеристике:

;

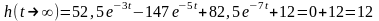• моделям в пространстве состояний (в установившемся режиме на входах интеграторов нули и u=1):

- каноническая форма:

-52,5 + 147 – 82,5=12

- нормальная форма:

x₂=0, x₃=-840, x₁=12; y=x₁=K=12.

• аналитической записи импульсной переходной характеристики:

;

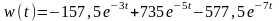проверяем:

.

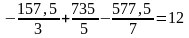Мы видим, что значение коэффициента усиления одинаково.