48.Достаточное условие

Теорема достаточное условие локального экстремума: Пусть в точке М0 возможного экстремума и некоторой её окрестности функция Z=f(x;y) имеет частные производные второго порядка. Обозначим: Составим матрицу: , обозначим = , тогда:

Если >0, то точка М0 – является точкой локального экстремума,

Если <0. то в точке М0 – экстремума нет,

Если >0, A>0, М0 – точка минимума,

Если >0, A<0, М0 – точка максимума.

49. Неопределённый интеграл

Определение: Если функция F(x) – первообразная для f(x) на промежутке (a;b), то множество функций F(x)+C – неопределённый интеграл от f(x).

∫f(x)dx=F(x)+C, где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, dx – переменная интегррования.

Первообразная

-

50. Основные свойства неопределённого интеграла:

1) Производная от неопределенного интеграла = подынтегральной функции.

2) Дифференциал от неопределённого интеграла = подынтегральному выражению.

3) Постоянный множитель м.б. вынесен из под знака интерала.

4) Интеграл от алгебраической суммы/разности функций = алгебраической сумме/разности интегралов. Справедливо для любого конечного количества слогаемых.

51.Замена переменных(Метод подстановки)

Методом подстановки (заменой переменной) называется метод, при котором введение новой переменной позволяет свести исходный интеграл к табличному.

Теорема: Пусть функция x=(t) определена и дифференцируема на некотором множестве Т, и пусть Х-множество значений этой функции. На множестве Х определена функция y=f(x), тогда если на Х функция f(x) имеет первообразную, то на Т справедлива формула:

52.Метод интегрирования по частям

Теорема: Пусть функции U(x) и V(x) определены и дифференцируемы, на множестве Х и пусть функция U’(x)*V(x) имеет первообразную на этом промежутке, тогда на Х функция U(x)*V’(x) так же имеет первообразную и справедлива формула: . Док-во: [U(x)V(x)]’=U’(x)V(x)+U(x)V’(x) => U(x)V’(x)=-U’(x)V(x)+[U(x)V(x)]’, интегрируя обе части получаем:

53.

36. Формулы Тейлора и Маклорена

Формула Тейлора для многочленов.

- остаточный член.

Если X стремится к Xo, то Rn(X) стремится к 0.

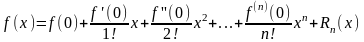- формула Маклорена.