9.Формула Крамера:

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы

Теорема: если определитель системы (1) отличен от нуля, то система имеет единственное решение, получаемое по формулам Крамера.

Правило Крамера. Система n уравнений с n переменными, определитель которой отличен от нуля, всегда имеет решение и притом единственное, определяемое следующим правилом: значение каждого из переменных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом переменном столбцом свободных членов.

10 Слау. Матрич метод.

AX=B

X=A^-1B (A^*. A11, A22 и т.д.) A^-1=1/detA * A^*

Если матрица А системы линейных уравнений невырожденная, т.е.

det A ¹ 0, то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.

20. Уравнения плоскости в пространстве.Уравнение плоскости, проходящей через данную точку Мо (хо, уо, zо) перпендикулярно вектору n=(А, В, С).

Общее ур-е плоскости

• Ур-е плоскости, проходящей через три данные точки

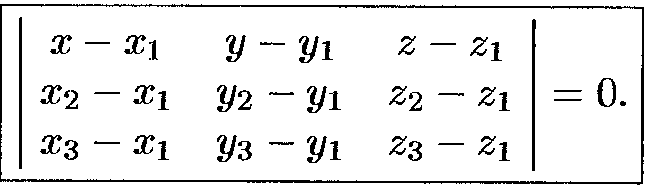
Ур-е плоскости в отрезках

Нормальное ур-е плоскости

21. Уравнения прямой в пространстве.

• Векторное ур-е прямой - 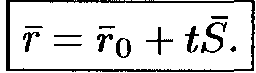, где S – направление вектора прямой, t – параметр.

• Параметрическое ур-е прямой -

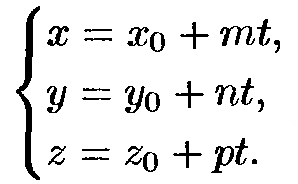
• Каноническое ур-е прямой -

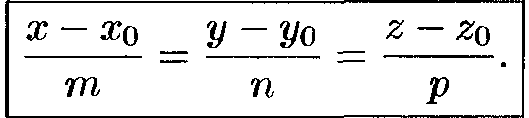
• Общие ур-я прямой -

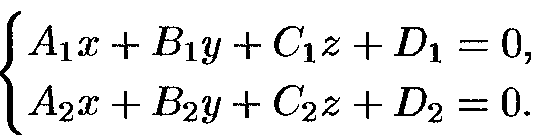
22. Прямая и плоскость в пространстве.

• Условие параллельности прямой и плоскости -

• Условие перпенидикулярности прям. и плоск. -

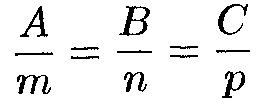
• Условие принадлежности прям. и плоск. -

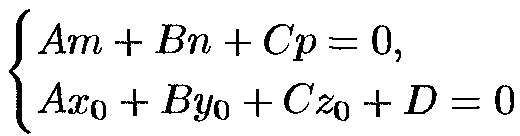
23. Функции одной переменной. Способы задания.

Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу x э X сопоставляет один и только один y э Y, называется функцией и записывается y=f(x), x э X.

Множество Х – область определения ф-ии f и обозначается D(f). Множество всех y э Y – мнж-во значений фу-ии f и обозначается E(f).

Если элементы множ-ва X и Y – действительные числа (R), то фу-ия f – числовая функция.

х-аргумент, y-зависимая переменная.

Способы задания фу-ии:

1. С помощью формулы

2. Графика

3. Таблицы

24. Предел числовой последовательности.

Числовая последовательность х₁, х₂, х₃,…х_n,… - это ф-ия х_n=f(n), заданная на множестве N. Кратко обозначается в виде {x_n}.

Послед-ть – ограниченная, если существует такое число M>0, что для любого n э N выполняется нерав-во |x_n|≤M. В противном случае послед-ть неогранич.

Послед-ть постоянная, если все её элементы равны одному и тому же числу c.

Число a – предел последовательности {x_n}, если для любого положительного числа ԑ найдётся такое натурал. число N, что при всех n>N выполняется нер-во |x_n-a|<ԑ. В этом случае пишут lim_n∞>8 x_n=a.

Надо написать, что такое число е!!!! чему равно и его формулу.

25. Предел функции в точке.

Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x −x0| < δ, справедливо неравенство |f(x) − A| < ε,   т.е. lim x->x0 f(x) = A

Пределы функции слева и справа – односторонние

26. Основные теоремы о пределах.

Lim x->x0 f(x) = a, lim x->x0 g(x) = b.

1. Lim ( f(x) + - g (x)) = lim x->x0 f(x) + - lim x->x0 g(x) = a+ - b.

2. Lim x->x0 (c f (x)) = c lim x->x0 f(x) = ca.

3. Lim x->x0 ( f(x) * g(x) ) = lim x->x0 f(x) * lim x->x0 g(x) = ab.

4. Lim x->x0 f(x) : g(x) = lim x->x0 f(x) : lim x->x0 g(x) = a:b; (b не равно 0).

5. Lim x->x0 f(x)^g(x) = f(x₀)^g(x₀⁾ = a^b.

27. Замечательные пределы.

При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел (Первый зам. Предел).

или Второй зам. Предел.

28. Бесконечно малая и Бесконечно большая функции.

ББФ.

Функция у=f(x) – ббф при x->x0, если для любого числа M>0 существует число δ= δ(M) >0, что для всех х, удовлетворяющих неравенству 0<|x-x0|< δ, выполняется неравенство |f(x)|>M. Записывают lim x->x0 f(x) = 8(бесконечность).

БМФ.

Функция y= f(x) – бмф при x->x0, если lim x->x0 f(x) = 0. Частное от деления бмф на функцию, имеющую отличный от нуля предел – бмф.

Алгебраическая сумма конечного числа бмфункций – бмф. Функция, обратная бмф – ббф и наоборот.

Произведение огранич. Фу-ии на бмф – бмф.

Произведение двух бмф – бмф.

Произведение бмф на число –бмф.