
- •16.Прямая на плоскости.Формы записи
- •5. Операции над матрицами
- •6.Вычисление определителей
- •6.Определитель 2 и 3 порядков.
- •7.Обратная матрица
- •8.Ранг матрицы. Способы вычисления.
- •9.Формула Крамера:
- •10 Слау. Матрич метод.
- •21. Уравнения прямой в пространстве.
- •22. Прямая и плоскость в пространстве.
- •23. Функции одной переменной. Способы задания.
- •29. Непрерывность функции в точке.
- •30. Точки разрыва функции. Их классификации.
- •31. Свойства функций, непрерывных на отрезке
- •32. Дифференцируемость функций.
- •33.Производная.Её геом. И мех. Смысл
- •34. Понятие дифференциала. Его связь с производной.
- •35. Применение дифференциала к приближенным вычислениям
- •37.Свойства функций, дифференцируемых на отрезке.Теорема Лагранжа
- •38. Свойства функций, дифференцируемых на отрезке.Теорема Коши.
- •39.Правило Лапиталя-Бернули.
- •40.Возрастание и убывание функции
- •41.Локальные экстремумы функции одной переменной.
- •42.Выпуклость функции. Точки перегиба
- •43. Асимптоты графика функций
- •44.ФНп.Частные производные
- •45.Полный дифференциал
- •47.Экстремумы
- •48.Достаточное условие
- •51.Замена переменных(Метод подстановки)
- •52.Метод интегрирования по частям
- •36. Формулы Тейлора и Маклорена
33.Производная.Её геом. И мех. Смысл
Понятие производной
Рассмотрим функцию y=f(x) на интервале (a;b). Возьмём на этом интервале точку х0 и приращение на оси Ох. Прямая, соединяющая 2 точки (х0;f(x0)) и (x0+x;f(x0+x))на графике функции называется секущей.
Угловой
коэффициент секущей равен отношению
приращения функции к вызвавшему его
приращению аргумента.
Производной
функции y=f(x)
называется предел отношения приращения
функции к вызвавшему его приращению
аргумента при стремлении последнего
к нулю (при условии, что этот предел
существует)

Если предел конечен, то производная конечная, если предел бесконечен, то производная бесконечна.
. Геометрический смысл производной
прямая y-y0=k(x-x0), угловой коэффициент которой равен производной функции в данной точке (k=f’(x0)) называется касательной к графику функции в данной точке.
При х0, значение х0+хх0, т.е. секущая стремиться занять положение касательной, так будем говорить, что касательная есть предельное положение секущей.
Геометрический
смысл производной состоит в том, что
она равна tg
угла наклона касательной.
Прямая,
перпендикулярная касательной в точке
касания называется нормалью.
 -уравнение
нормали в точке х0.
-уравнение
нормали в точке х0.
Мех.смысл: скорость прямолинейного движения материальной точки в момент времени Т есть производная от пути S по времени Т.
34. Понятие дифференциала. Его связь с производной.
Дифференциал функции - это произведение производной f ’( x0 ) и приращения аргумента :
df = f ’( x0 ) · .
Операция вычисления производной функции называется дифференцированием.
Функция y=f(x), называется дифференцируемой в точке х0, если её приращение функции (y) может быть представлено: y=A*x+(x)x, где А-число, не зависящее от х, а (x) – бесконечно малая функция.
Теорема:
для того, чтобы функция y=f(x)
была дифференцируемой в точке х0
необходимо и достаточно, чтобы она
имела в этой точке конечную производную.
Док-во: необходимость: пусть функция
дифференцируема в точке, тогда её
приращение может быть записано как
y=A*x+(x)x.
Разделим всё на x:
 ,
переходя к пределу:
,
переходя к пределу: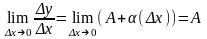 .
По определению в точке х0 имеется
конечная производная А. Достаточность:
пусть существует конечная производная
функции y=f(x)
в точке х0:
.
По определению в точке х0 имеется
конечная производная А. Достаточность:
пусть существует конечная производная
функции y=f(x)
в точке х0:
 ,
,
Теорема
(второе определение непрерывности):
если функция y=f(x)
дифференцируема в точке х0, то она и
непрерывна в этой точке. Док-во: т.к.
функция дифференцируема в точке, то её
приращение можно записать y=A*x+(x)x,
найдем предел:
 ,
это означает, что функция в точке
непрерывна. Обратное НЕ верно.
,
это означает, что функция в точке
непрерывна. Обратное НЕ верно.
35. Применение дифференциала к приближенным вычислениям
Δy можно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dy или Δy»f'(x0)·Δx.
