3.3. Примеры математических моделей

3.3.1. Модель целенаправленной системы

Используя теоретико-множественные представления, модель самой абстрактной системы можно записать в виде кортежа (последовательности) двух множеств:

S  < A, R > (3.1)

где A = {a_i} – множество элементов, а R = {r_j} – множество связей (отношений) между элементами.

Если известно, что элементы множества неоднородны, то это можно учесть в определении, добавляя в кортеж разные (под-) множества элементов:

S  < A, B, R >

где B ={b_k} – множество элементов другого типа (отличного от A).

В общем случае системный кортеж можно расширять за счёт добавления следующих множеств:

Q_A – множество свойств элементов ( a_i  A),

Q_R – множество свойств связей (q_j  R),

Z – цель, множество или структура целей системы,

SR – среда, в которой существует (функционирует) целеустремлённая система,

T – период времени, в течение которого существует целеустремлённая система,

N – наблюдатель, т. е. лицо, представляющее объект или процесс в виде системы при их исследовании или принятии решения,

L_N – язык, который наблюдатель использует для представления системы.

В результате будет построена расширенная модель целенаправленной системы:

S  < A, Q_A, R, Q_R, Z, SR, T, N, L_N > (3.2)

Взгляд на определение системы как на средство ее исследования и создания позволил ввести определение, в котором система не расчленяется на элементы, т.е. не разрушается, что делается в вышеприведенном определении, а представляется как совокупность укрупненных компонент, принципиально необходимых для её существования и функционирования:

S  < {Z},{STR},{TECH},{COND}> (3.3)

где Z = {z} - совокупность или структура целей;

STR = {STR_пр, STR_орг, ... } - совокупность структур, реализующих цели; STR_np - производственная, STR_орг, - организационная и т. п.

ТЕСН - {meth, means, alg, ... } - совокупность технологий (методы meth, средства means, алгоритмы alg и т.п.), реализаующих систему;

COND - {_ex, _in} - условия существования системы, т.е. факторы, влияющие на ее создание и функционирование (_ex‑внешние, _in – внутренние).

Такое определение особенно полезно для информационных систем автоматизированного управления.

3.3.2. Модель абстрактной системы с неопределённой структурой

З десь рассматривается модель системы с неопределенной структурой, т.е. системы элементы и связи которой не определены, [4]. Такая система представляется моделью «чёрного ящика», на вход которого подаются входные воздействия, и по определённому набору заранее известных свойств (параметров) системы исследуется её реакция на входные воздействия (рис. 3.1).

x+ x^‑

Рис. 3.1. Модель абстрактной системы с неизвестной структурой («чёрный ящик»)

Обозначим:

• набор входных воздействий (входов) в системе х⁺ и всю их допустимую совокупность Х⁺, х⁺Х⁺;

• набор выходных воздействий (выходов) в системе х^‑ и всю их возможную совокупность Х ^‑, х^‑Х ^‑;

• набор параметров, характеризующих свойства системы, постоянные во все время рассмотрения, и влияющих на выходные воздействия системы а и всю их допустимую совокупность А, аA;

• набор параметров, характеризующих свойства системы, изменяющиеся во время ее рассмотрения (параметры состояния), у и всю их допустимую совокупность Y, yY;

• параметр (или параметры) процесса в системе t и всю их допустимую совокупность Т, tT;

• правило S (функция, оператор) определения параметров состояния системы по входам х⁺, постоянным параметрам а и параметру процесса t. Заметим, что всегда следует различать величины и правило их определения. Так запись y=S(x⁺, a, t) означает нахождение параметров по этому правилу, в то время как о величине у можно говорить и вне правила ее определения;

• правило V (функция, оператор) определения выходных характеристик системы по входам х⁺, постоянным параметрам а, параметру процесса t и параметрам состояния у, т. е. х^‑ = V(x⁺, a, t, y);

• правило 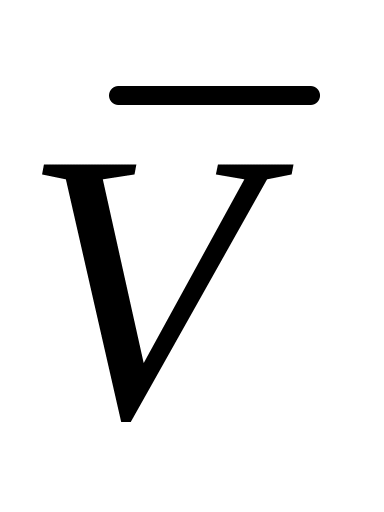(функция, оператор) определения выходных характеристик системы по входам х⁺, постоянным параметрам а и параметру процесса. Указанное правило может быть получено подстановкой правила S в правило V, что дает исключение из него параметров состояния: x^‑= (x⁺, a, t).

На основе введения вышеуказанных воздействий, параметров и правил модель «чёрного ящика» может быть записана как кортеж

 = <x⁺, x^‑, a, t, y, S, V, >, x⁺  X⁺, x ^‑  X ^‑, a  A, t  T, y  Y (3.4)