4.6. Моделирование по методу Монте-Карло
Моделирование по методу Монте-Карло определяется как процедура, в которой используются случайные числа, то есть случайные величины U(0,1). Такая процедура предназначена для решения стохастических и детерминистических задач, в которых течение времени не играет особой роли. Следовательно, моделирование по методу Монте-Карло является скорее статическим, чем динамическим. Хотя иногда утверждают, что метод Монте-Карло применим к любому типу моделирования, в котором используются случайные числа, лучше считать его использование более ограниченным. Название метода Монте-Карло появилось во время второй мировой войны, когда этот подход был применен к проблемам, связанным с разработкой атомной бомбы.
В качестве примера моделирования по методу Монте Карло приведём оценку интеграла
где g(x) является действительной функцией, которую нельзя интегрировать аналитически. На практике моделирование по методу Монте-Карло вряд ли будет использоваться для оценки одного единственного интеграла, так как для этого существуют более эффективные методы численного анализа. Вероятнее, что он будет применяться для решения задач на кратные интегралы с нерегулярной подынтегральной функцией.
Покажем, как детерминистическая задача может быть решена с помощью моделирования методом Монте-Карло. Пусть Y будет случайной величиной (b - a)g(X), где X ‑ непрерывная случайная величина, распределенная равномерно в интервале [а, b] (плотность распределения вероятностей такой случайной величины обозначается как U[a,b], U – от англ. uniform ‑ равномерный). Тогда математическое ожидание значения Y
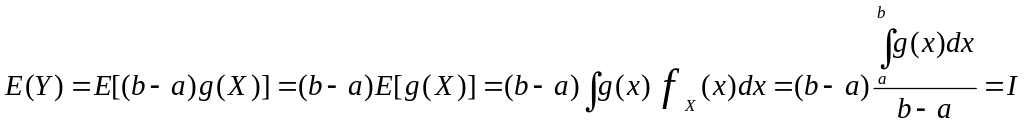
где fX(x) = 1/(b ‑ а) ‑ плотность распределения вероятностей случайной величины X, равномерно распределённой в интервале [a, b]. Таким образом, задача оценки интеграла упрощена до оценки ожидаемой величины E(Y). В частности, оценим E(Y) = I по выборочному среднему:
(n)
=
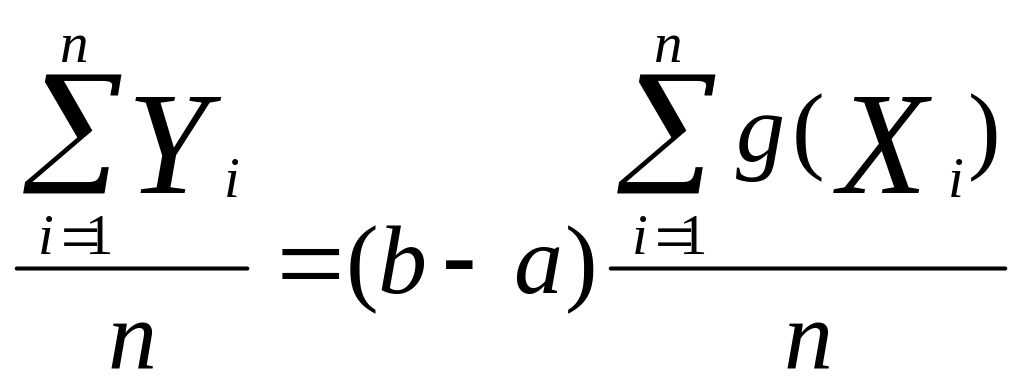
где X1, Х2,..., Хn ‑ независимые и одинаково распределенные случайные величины U[a, b]. Выборочное среднее (n) можно рассматривать как площадь прямоугольника с длиной (b ‑ а) и высотой I/(b ‑ а), которое является непрерывным средним g(x) между [а, b]. Более того, можно показать, что Е[ (n) = 1], то есть (n) является несмещенной оценкой I, а дисперсия Var[ (n)] = Var(Y)/n. Допустим, что дисперсия Var(Y) является конечной, из чего следует, что значение (n) будет сколь угодно близко к I для достаточно большого значения n с вероятностью, равной 1.
Для демонстрации описанной выше схемы в численном отношении предположим, что необходимо оценить интеграл
который, как показывают элементарные вычисления, может иметь значение 2. Результаты применения моделирования по методу Монте-Карло для оценки этого интеграла при разных значениях n приведены в табл. 4.2.
Таблица 4.2.
(n)
при разных значениях n,
полученные в результате применениямоделирования
по методу Монте-Карло для оценки интеграла
n |
10 |
20 |
40 |
80 |
160 |
(n) |
2,213 |
1,951 |
1,948 |
1,989 |
1,993 |
В настоящее время моделирование по методу Монте-Карло широко применяется при решении определенных задач статистики, которые не поддаются аналитической обработке. Этот тип моделирования применялся для оценки критических значений или достоверности критерия проверки статистических гипотез. Примером такого применения является определение критических значений критерия Колмогорова-Смирнова для непараметрической проверки гипотезы нормальности.