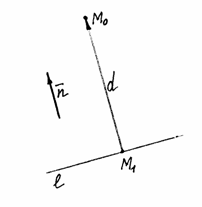
22.Расстояние от точки до прямой.

Пусть прямая  на плоскости задана уравнением  и точка  имеет координаты  (рис. 25). Обозначим  – основание перпендикуляра, опущенного из точки  на прямую , ,  – расстояние от точки  до прямой . Тогда , а  – нормальный вектор прямой. Рассмотрим скалярное произведение . С одной стороны, , так как , следовательно, угол между ними или . С другой стороны, , но точка , поэтому ее координаты удовлетворяют уравнению , откуда , поэтому . Приравнивая выражения, получим

. Тогда  или

.                                                 (2.21)

23.Эллипс

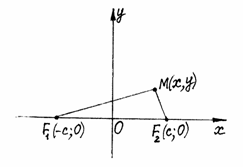
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Обозначим фокусы F₁, F₂, расстояние между ними – 2с, постоянную из определения – 2а (по условию 2а > 2с, то есть а > с). Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокусы и точка О находилась на середине отрезка F₁F₂. В такой системе координат F₁(-с; о), F₂(с; о) (рис. 28).

 

каноническое уравнение эллипса:

 

Уравнение содержит только четные степени х, у, следовательно, кривая симметрична относительно осей координат. В первой координатной четверти уравнение имеет вид  при возрастании х от 0 до а у убывает от в до 0. Учитывая симметрию, можно сделать вывод о форме эллипса (рис. 29).

 

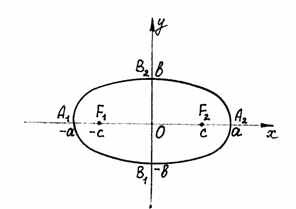
Оси симметрии эллипса называются осями эллипса, точка их пересечения 0 – центром эллипса. Ось, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с осями называются вершинами эллипса (А₁, А₂, В₁, В₂). Отрезки А₁А₂ и В₁В₂, а также их длины 2а и 2в называются соответственно большой и малой осями эллипса. Числа а и в называются соответственно большой и малой полуосями эллипса.

Отношение половины расстояния между фокусами к большой полуоси называется эксцентриситетом эллипса.  < 1.

Эксцентриситет характеризует форму эллипса: чем меньше эксцентриситет, тем меньше его малая полуось в отличается от большой полуоси а, то есть тем меньше вытянут эллипс вдоль фокальной оси

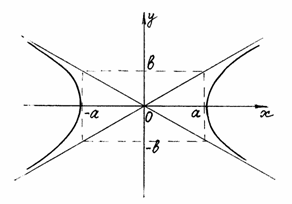
24.Гипербола.

Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

каноническое уравнение гиперболы:

 

(2.23)

 

Кривая симметрична относительно осей координат, так как уравнение содержит только четные степени х, у. В первой координатной четверти уравнение имеет вид  х  а; при возрастании х от а до + у возрастает от 0 до +. Учитывая симметрию, можно сделать вывод о форме гиперболы

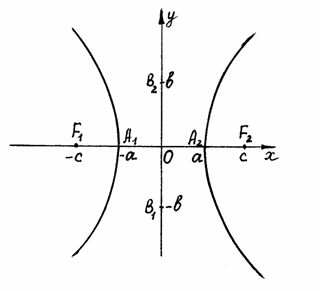
Рис. 30

Полагая в каноническом уравнении у = 0, найдем точки пересечения гиперболы с осью ОХ: х = а. При х = 0 уравнение не имеет решений, то есть с осью ОУ гипербола не пересекается. Точки А₁(-а; 0) и А₂(а; 0) называются вершинами гиперболы. Фокальная ось (ось, на которой лежат фокусы) называется действительной осью гиперболы, а перпендикулярная ей ось – мнимой осью. Действительной осью называется также отрезок А₁А₂ и его длина 2а. Отрезок, соединяющий точки В₁(0; -в) и В₂(0; в), а также его длина 2в называются мнимой осью гиперболы. Числа а и в называются соответственно действительной и мнимой полуосями.

Отношение  называется эксцентриситетом гиперболы.  > 1.

Эксцентриситет характеризует форму гиперболы: чем меньше эксцентриситет, тем меньше отношение полуосей гиперболы, то есть тем сильнее вытянут ее основной прямоугольник относительно фокальной оси

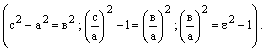
Рассмотрим часть гиперболы, расположенную в первой четверти:  Покажем, что точки этого графика, расположенные на достаточно большом расстоянии от начала координат, сколь угодно близки к прямой  Пусть М(х, у) и N(х, У) – точки с одной и той же абсциссой, лежащие соответственно на гиперболе и на прямой  (рис. 31). Рассмотрим разность ординат этих точек:

 

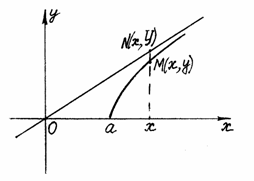
Рис. 31

 

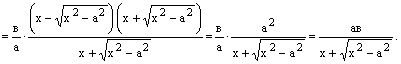
Очевидно, что при неограниченном возрастании х эта разность стремится к нулю, то есть точки М и N неограниченно сближаются. Из симметрии гиперболы относительно осей координат следует, что этим же свойством обладает прямая  Прямые  и  называются асимптотами гиперболы.

На рисунке 32 показано, как с помощью основного прямоугольника гиперболы (это прямоугольник со сторонами длиной 2а и 2в, параллельными осями координат) построить асимптоты гиперболы. Из рисунка видно также взаимное расположение гиперболы и ее асимптот.