18.Общее уравнение прямой на плоскости. Случаи расположения прямой относительно осей координат.Уравнение прямой в отрезках.

Пусть  – заданная точка на прямой ,  – вектор, перпендикулярный прямой , его называют нормальным вектором прямой, и пусть  – произвольная точка прямой  (рис. 20). Тогда , , то есть

.                                      

(2.12) – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

  Рис. 20

Раскрыв скобки и сгруппировав слагаемые в (2.12), получим . Обозначим , уравнение примет вид

.   – общее уравнение прямой на плоскости.

Если в уравнении (2.13) , , , то, перенеся слагаемое С в правую часть и разделив на него обе части уравнения, получим

, или 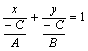. Обозначим , , тогда уравнение примет вид

                                                         (2.14)

(2.14) – уравнение прямой в отрезках, здесь a и b – отрезки, отсекаемые прямой на осях координат (рис. 21): из уравнения (2.13) при  получим , а при   .

 

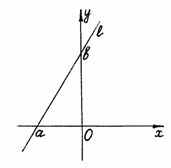
Рис. 21

19.Уравнение прямой с угловым коэффициентом.Уравнение прямой, проходящей через данную точку в данном направлении.

.                                                         (2.15)

(2.15) – каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.

.                                               (2.18)

 

Рис. 23

Выразив из (2.18) :  и обозначив , получим

.                                                       (2.19)

(2.18), (2.19) – уравнения прямой с угловым коэффициентом. В уравнении (2.19)  – ордината точки пересечения прямой с осью .

20.Уравнение прямой, проходящей через две данные точки (на плоскости).

Пусть на прямой  заданы две точки  и . Тогда вектор  является направляющим вектором прямой и, используя уравнение (2.15), можно записать

.                                          (2.17)

(2.17) – уравнение прямой, проходящей через две данные точки.

21.Угол между двумя прямыми (на плоскости). Условия параллельности и перпендикулярности прямых.

Пусть прямые  и  заданы соответственно уравнениями , , где , . Обозначим  угол между прямыми:  (рис. 24). Тогда , .

 

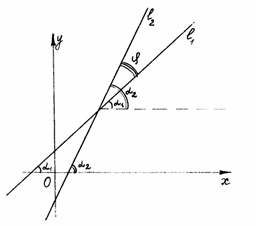
Рис. 24

Таким образом,

.                                                  (2.20)

Если , то , а следовательно, , то есть k₁= k₂.

Если , то ,  не определен, , следовательно, , или .

Если прямые  и  заданы соответственно уравнениями

, , где ,  – нормальные векторы прямых, то 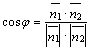, или .

Если , то , следовательно, .

Если , , то есть .