
- •2.Понятие определителя n-ого порядка. Схемы вычисления определителей 2-ого и 3-ого порядков
- •3.Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя.
- •4.Свойства определителей. Вычисление определителей порядка выше 3-его при помощи свойств определителя и теоремы о разложении определителя.
- •5.Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Алгоритм вычисления обратной матрицы.
- •6.Ранг матрицы. Преобразования матрицы, не меняющие ее ранга.
- •7.Системы m линейных уравнений с n неизвестными. Основные понятия. Матричный вид системы линейных уравнений.
- •8.Системы n линейных уравнений с n неизвестными. Метод обратной матрицы.
- •9.Системы линейных уравнений с n неизвестными.Формулы Крамера.
- •10.Метод Гаусса решения системы m линейных уравнений с n неизвестными.
- •12.Системы линейных однородных уравнений. Существование ненулевого решения.
- •15.Скалярное произведение векторов и его свойства.Условие перпендикулярности векторов.Угол между векторами.
- •16.Векторное произведение и его свойства.
- •17.Смешанное произведение и его свойства.Условие компланарности векторов.
- •18.Общее уравнение прямой на плоскости. Случаи расположения прямой относительно осей координат.Уравнение прямой в отрезках.
- •19.Уравнение прямой с угловым коэффициентом.Уравнение прямой, проходящей через данную точку в данном направлении.
- •20.Уравнение прямой, проходящей через две данные точки (на плоскости).
- •21.Угол между двумя прямыми (на плоскости). Условия параллельности и перпендикулярности прямых.
- •22.Расстояние от точки до прямой.
- •23.Эллипс
- •24.Гипербола.
- •25.Парабола.
- •26.Поворот и параллельный перенос осей координат (на плоскости).
- •28.Случаи расположения плоскости относительно осей координат.Уравнение плоскости в отрезках.
- •29.Условие параллельности и перпендикулярности плоскостей. Угол между плоскостями.
- •30.Уравнение прямой в пространстве,как линии пересечения двух плоскостей. Канонические уравнения прямой в пространстве.
- •31.Уравнения прямой в пространстве, проходящей через две данные точки. Параметрические уравнения прямой в пространстве.
- •33.Предел числовой последовательности.
- •34.Предел функции на бесконечности.
- •32.Угол между прямой и плоскостью
- •35.Предел функции в точке.
- •36.Бесконечно малые функции. Связь бесконечно малой функции и функции, имеющей предел.Свойства бесконечно малых функций.
- •37.Бесконечно большие функции.Их свойства.Теорема о связи бесконечно большой и бесконечно малой функций.
- •38.Теорема о единственности предела.Основные теоремы о пределах.Предел сложной функции.
- •Теорема о пределе сложной функции.
- •39.Признаки существования пределов.
- •Теорема о сохранении функцией знака своего предела
- •40.Первый замечательный предел.
- •41. Сравнение бесконечно малых функций. Примеры эквивалентных бесконечно малых функций.
- •42.Второй замечательный предел.Число е.Важные пределы как следствие второго замечательного предела.
- •43.Задача о непрерывном начислении процентов.
- •44.Непрерывность функции в точке.Приращение функции,приращение аргумента.Свойства функций, непрерывных в точке.
- •45.Непрерывность функции на отрезке.
- •46.Классификация точек разрыва.
- •47.Задача о скорости неравномерного прямолинейного движения.
- •48.Задача о касательной, приводящая к понятию о производной.
- •49.Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции. Примеры недифференцируемых функций в точке.
- •Замечание
- •54.Производная степенной функции. Логарифмическая производная.
- •55.Производные высших порядков.
12.Системы линейных однородных уравнений. Существование ненулевого решения.
Рассмотрим однородную систему линейных уравнений
![]()
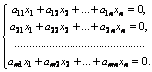 (1.19)
(1.19)
Такая система всегда совместна, так как этой системе удовлетворяют значения х1=х2=…=хn=0. Это решение системы называют тривиальным.Теорема. Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.Доказательство. По теореме Кронекера-Капелли, если r=n, то система имеет единственное решение. А так как система (1.19) имеет всегда тривиальное решение, то в этом случае оно и единственно, то есть при r=n система имеет лишь тривиальное решение.При r<n система является неопределенной, то есть имеет бесчисленное множество решений, в том числе и нетривиальное.Замечание. Если m=n, то есть число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие r<n в этом случае означает, что определитель системы, то есть det А=0, что следует из определения ранга матрицы.
Пример. Решить систему

Решение. Составим матрицу системы
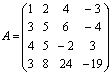
и методом элементарных преобразований найдем ранг
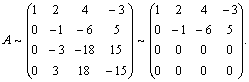 r=2.
r=2.
Выберем
в качестве базисного минор
![]() Тогда
укороченная система имеет вид
Тогда
укороченная система имеет вид
![]()
Полагая х3=с1, х4=с2, находим х2=-6с1+5с2, а х1=-4с1+3с2+2(6с1-5с2)=8с1-7с2. Общее решение системы
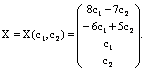 (1.20)
(1.20)
Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что свободным неизвестным дают последовательно значения
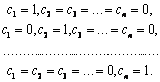
13.Вектор,
как геометрический объект.Коллинеарные
и компланарные векторы.Координаты
вектора.Длина вектора.Направляющие
косинусы.Вектором
называется направленный отрезок.
Обозначается вектор
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
AB,
a
(А
– начало вектора, В
– его конец).Нулевым
вектором
(обозначается
,
AB,
a
(А
– начало вектора, В
– его конец).Нулевым
вектором
(обозначается
![]() )
называется вектор, начало и конец
которого совпадают.Расстояние между
началом и концом вектора называется
его длиной,
или модулем,
или абсолютной
величиной
(обозначается
)
называется вектор, начало и конец
которого совпадают.Расстояние между
началом и концом вектора называется
его длиной,
или модулем,
или абсолютной
величиной
(обозначается
![]() ,
,
![]() ).Векторы
называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых (обозначают
).Векторы
называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых (обозначают
![]() ,
а также
,
а также
![]() ,
если векторы сонаправлены, и
,
если векторы сонаправлены, и
![]() ,
если они противоположно направлены).Векторы
называются компланарными,
если они лежат в одной плоскости или в
параллельных плоскостях. Два
вектора называются равными,
если они сонаправлены (
)
и имеют равные длины (
,
если они противоположно направлены).Векторы
называются компланарными,
если они лежат в одной плоскости или в
параллельных плоскостях. Два
вектора называются равными,
если они сонаправлены (
)
и имеют равные длины (
![]() ).
Обозначают
).
Обозначают
![]() .
Для
каждого вектора
,
отличного от нулевого вектора, существует
противоположный
вектор, который обозначается
.
Для
каждого вектора
,
отличного от нулевого вектора, существует
противоположный
вектор, который обозначается
![]() и
удовлетворяет условиям:
и
удовлетворяет условиям:
![]() ,
,
![]() .
.
Рассмотрим
декартову прямоугольную систему
координат Oxyz.
Обозначим
![]() ,
,
![]() ,
,
![]() –
единичные векторы,
направленные соответственно вдоль
осей Ox,
Oy,
Oz
(орты осей). Эти векторы называются
декартовым
прямоугольным базисом в
пространстве. Пусть
–
произвольный вектор в пространстве.
Перенесем его начало в точку O
(
–
единичные векторы,
направленные соответственно вдоль
осей Ox,
Oy,
Oz
(орты осей). Эти векторы называются
декартовым
прямоугольным базисом в
пространстве. Пусть
–
произвольный вектор в пространстве.
Перенесем его начало в точку O
(
![]() )
и построим прямоугольный параллелепипед,
в котором вектор
является
диагональю (рис. 11). Тогда
)
и построим прямоугольный параллелепипед,
в котором вектор
является
диагональю (рис. 11). Тогда
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() –
составляющие вектора
по
осям Ox,
Oy,
Oz.
Но
–
составляющие вектора
по
осям Ox,
Oy,
Oz.
Но
![]() ,
аналогично
,
аналогично
![]() ,
,
![]() .
.
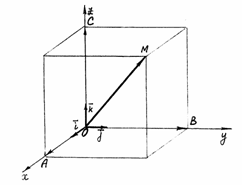
Рис. 11
Обозначая
![]() ,
,
![]() ,
,
![]() ,
получим
,
получим
![]() .
.
Это
равенство называется разложением
вектора
по
базису
,
![]() ,
,
а
числа
,
,
а
числа
![]() ,
,
![]() ,
,
![]() называются
координатами
вектора
в
этом базисе, или декартовыми прямоугольными
координатами вектора. Пишут
называются
координатами
вектора
в
этом базисе, или декартовыми прямоугольными
координатами вектора. Пишут
![]() или
или
![]() .
.
Таким образом, прямоугольные декартовы координаты вектора – это его проекции на соответствующие оси координат.
Зная координаты вектора, легко выразить его длину:
![]() (2.2)
(2.2)
(квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений).
Если
![]() ,
где
,
где
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
или
,
или
![]() –
(2.3)
–
(2.3)
так выражаются координаты вектора через координаты его начала и конца. Из свойств проекций (а координаты вектора – это его проекции на оси координат) следует:
если
![]() ,
,
![]() ,
,
![]() ,
то
,
то
1)
![]() ,
,
![]() ,
,
![]() –
равные векторы имеют соответственно
равные координаты;
–
равные векторы имеют соответственно
равные координаты;
2)
![]() –
при сложении векторов их координаты
складываются, при вычитании – вычитаются;
–
при сложении векторов их координаты
складываются, при вычитании – вычитаются;
3)
![]() –
при умножении вектора на число его
координаты умножаются на это число;
Направление вектора в пространстве
определяется углами
–
при умножении вектора на число его
координаты умножаются на это число;
Направление вектора в пространстве
определяется углами
![]() ,
которые вектор образует с осями координат
(рис. 12). Косинусы этих углов называются
направляющими
косинусами вектора:
,
которые вектор образует с осями координат
(рис. 12). Косинусы этих углов называются
направляющими
косинусами вектора:
![]() ,
,
![]() ,
,
![]() .
.
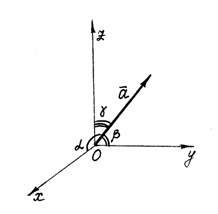
Рис. 12
Из
свойств проекций:
![]() ,
,
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() ,
,
![]() .
(2.5)
.
(2.5)
Легко показать, что
1)
![]() ;
;
2)
координаты любого единичного вектора
совпадают с его направляющими косинусами:
![]() .
.
14.Линейные операции над векторами.Условие коллинеарности векторов, выраженное в координатах. Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Сложение
векторов.
Пусть
и
![]() –
два произвольных вектора. Возьмем
произвольную точку О
и построим вектор
–
два произвольных вектора. Возьмем
произвольную точку О
и построим вектор
![]() ;
затем от точки А
отложим вектор
;
затем от точки А
отложим вектор
![]() .
Вектор
,
соединяющий начало первого слагаемого
вектора с концом второго, называется
суммой
этих векторов и обозначается
.
Вектор
,
соединяющий начало первого слагаемого
вектора с концом второго, называется
суммой
этих векторов и обозначается
![]() (рис.
1).
(рис.
1).
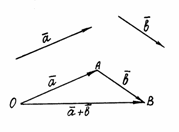
Рис. 1
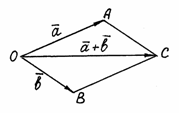
Ту
же сумму можно получить иным способом.
Отложим от точки О
векторы
и
![]() .
Построим на этих векторах как на сторонах
параллелограмм ОАСВ.
Вектор
–
диагональ параллелограмма – является
суммой векторов
и
(рис.
2).
.
Построим на этих векторах как на сторонах
параллелограмм ОАСВ.
Вектор
–
диагональ параллелограмма – является
суммой векторов
и
(рис.
2).
Вычитание
векторов. Разностью
![]() векторов
и
называется
такой вектор
векторов
и
называется
такой вектор
![]() ,
который в сумме с вектором
дает
вектор
:
,
который в сумме с вектором
дает
вектор
:
![]()
![]() .
.
Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
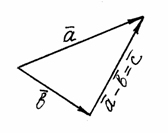
Рис.
4Таким образом, если на векторах
и
,
отложенных из общей точки О,
построить параллелограмм ОАСВ,
то вектор
,
совпадающий с одной диагональю, равен
сумме
,
а вектор
![]() ,
совпадающий с другой диагональю, –
разности
(рис.
5).
,
совпадающий с другой диагональю, –
разности
(рис.
5).
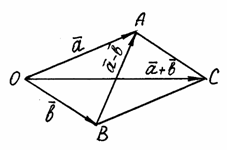
Рис. 5
Умножение
вектора на число. Произведением
вектора
на
действительное число
![]() называется
вектор
(обозначают
называется
вектор
(обозначают
![]() ),
определяемый следующими условиями:
),
определяемый следующими условиями:
1)
![]() ,
,
2)
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Очевидно,
что при
![]()
![]() .
.
Построим,
например, векторы
![]() и
и
![]() для
заданного вектора
(рис.
6).
для
заданного вектора
(рис.
6).
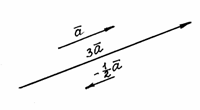
Рис. 6
Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство :
![]() 4)
4)
![]() ,
,
![]() ,
,
![]() ,
то есть
,
то есть
![]() –
(2.4)
–
(2.4)
координаты коллинеарных векторов пропорциональны.
(2.1)
Свойства линейных операций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
![]() ;
;
Разложение вектора по базису.
Определение.
Пусть
![]() –
произвольный вектор,
–
произвольный вектор,
![]() –
произвольная система
векторов. Если выполняется равенство
–
произвольная система
векторов. Если выполняется равенство
![]() ,
(1)
,
(1)
то говорят, что
вектор
представлен
в виде линейной комбинации данной
системы
векторов. Если данная система
векторов
является
базисом векторного
пространства, то равенство
(1) называется разложением вектора
по
базису
.
Коэффициенты линейной комбинации
![]() называются
в этом случае координатами вектора
относительно
базиса
.
называются
в этом случае координатами вектора
относительно
базиса
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
