8.Системы n линейных уравнений с n неизвестными. Метод обратной матрицы.

Пусть число ур-ний системы (2.3) равно числу переменных, т.е. m=n. Тогда м-ца явл. Квадратной, а её определитель называется определителем системы.

Рассмотрим линейную систему (2.3): 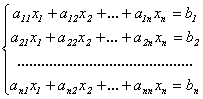 и введем следующие обозначения:

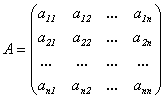- матрица системы, 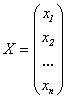- столбец неизвестных,

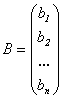- столбец свободных членов. Тогда систему (2.3) можно записать в виде матричного уравнения:

АХ = В.         

9.Системы линейных уравнений с n неизвестными.Формулы Крамера.

Введем следующие обозначения. Пусть ,  -- определитель матрицы, полученной из матрицы заменой столбца с номером на столбец свободных членов, :

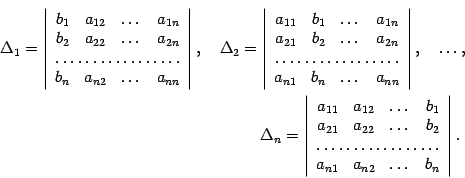
Теорема (правило Крамера). Если определитель системы Д <>0, то рассматриваемая система имеет одно и только одно решение, причём это решение находится по формулам:

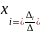,где ∆i находится заменой в определителе i-ого столбца на столбец свободных членов.

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение - на A₂₁ и 3-е - на A₃₁:

Пусть матрица А – невырожденная, тогда существует обратная к ней матрица

Умножим обе части равенства (3.1) слева на  Получим

                 

Но  тогда , а поскольку          (3.2)

Итак, решением матричного уравнения (3.1) является произведение матрицы, обратной к А, на столбец свободных членов системы (2.3).

Формулы Крамера являются решением с-мы поэлементно.

Обратная матрица находится по формуле

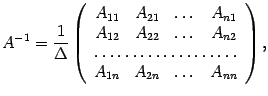
где -- алгебраические дополнения. Тогда из (15.3) следует, что

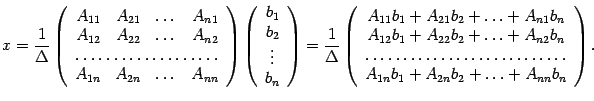Заметим, что по формуле (14.13) разложение определителя по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому , откуда и следует утверждение теоремы.

10.Метод Гаусса решения системы m линейных уравнений с n неизвестными.

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида, из которых последовательно, начиная с последних по номеру переменных, находятся все остальные переменные.

решения системы m линейных уравнений с n неизвестными. Если строки расширенной м-цы линейно независимы, то ранг м-цы равен числу её уравнений, т.е. r=m, если – линейно независимы, то r<m

Пример2 . Исследовать совместность и найти общее решение системы

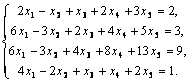
Решение. Произведем элементарные преобразования расширенной матрицы системы

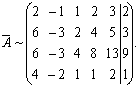
Умножив первую строку матрицы на –3, сложим ее со второй и третьей строками, а, умножив на –2, сложим ее с четвертой строкой.

Тогда имеем

Сложим теперь вторую строку этой матрицы с третьей и вычтем ее из четвертой:

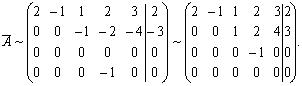Так как расширенная матрица системы  и матрица системы А содержат три ненулевых строки, то  Система совместна и, так как ранг матрицы  меньше числа неизвестных системы, то система имеет множество решений.

Выберем в качестве базисного минора

 Тогда неизвестные х₂, х₃, х₄ – базисные, а х₁ и х₅ – свободные. Укороченная система имеет вид

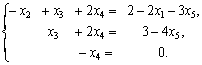
Положим х₁=с₁, х₅=с₂. Тогда система примет вид

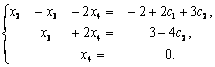
Так как х₄=0, то из второго уравнения этой системы х₃=3-4с₂.

Подставляя х₄ и х₃ в первое уравнение, получим

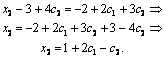
Следовательно, общее решение исходной системы имеет вид

                                           

.Исследование систем линейных уравнений. Теорема Кронекера-Капелли.

Всякий детерминант минора матрицы A, отличный от нуля, размер которого равен рангу этой матрицы, называется базисным минором. Т.е. иными словами ранг матрицы A это наивысший отличный от нуля минор.

1°. Линейная зависимость строк матрицы.

Пусть P — поле.

Def1 Будем говорить, что строка B=(b₁, …, b_n) b_i Є P является линейной комбинацией строк A₁=(a₁₁, …, a_1n,), …, A_k=(_k1, …, a_kn,), a_ij Є P, если для некоторых α₁,…, α_k Є P справедливо

b_j=α₁a_ij + … + α_kj, j=1, …, n. (1)

Это равенство удобно записать в матричном виде:

B=α₁A₁+ … + α_kA_k. (1’)

Def2 Строки A₁=(a₁₁, …, a_1n,), …, A_k=(_k1, …, a_kn,) назовем линейно зависимыми, если  такие  одновременно не равные нулю, такие что из В=О НЕ СЛЕДУЕТ равенство всех коэффицентов нулю(т.е.αi может быть отличен от нуля)

Строки, не являющиеся линейно зависимыми, являются линейно независимыми. Иными словами, A₁, …, A_k — линейно независимы, если равенство  возможно, лишь когда все коэф. равны нулю.

Минор r-го порядка, отличный от нуля, называется базисным минором, строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами.

Теорема (теорема о базисном миноре): Базисные строки (столбцы) линейно независимы. Любая строка (любой столбец) матрицы A является линейной комбинацией базисных строк (базисных столбцов).

Док-во (Рассуждение для строк):

Покажем, что базисные строки линейно независимы

Если первая, например, строка — линейная комбинация остальных, то вычитая в базисном миноре из первой строки линейную комбинацию остальных, получим нулевую строку базисный минор нулевой — противоречие.

Докажем, что  строка A является линейной комбинацией остальных. Т.к. при переменах строк и столбцов определитель сохраняет свойство равенства (неравенства) нулю, то будем считать, что базисный минор составлен из первых r строк и r столбцов.

Рассмотрим определитель (r+1) порядка

Здесь Если то две одинаковые строки или столбца и определитель равны нулю. то это минор порядка r+1  равен нулю. Итак определитель равен нулю  k и j.

Разложим его по r+1 столбцу. Отметим, что

 и коэффициенты A_ij не зависят от выбора j, т.е.

 что означает, что k-ая строка является линейной комбинацией первых r.

Теорема Кронекера-Капелли

Система линейных уравнений совместна тогда и только тогда, когда ранг м-цы системы равен рангу расширенной м-цы этой системы.

Не приводя строгого доказательства теоремы, поясним его. В процессе преобразования системы уравнений (2.1) к виду (2.10), т.е. элементарных преобразований м-цы системы А и расширенной м-цы А₁, ранги этих м-ц не изменяются. В случае, когда система совместна, ранг м-цы и ранг расширенной м-цы системы (2.10), так же как и данной системы (2.1) совпадают.

Для совместных систем линейных уравнений верны следующие теоремы:

1. Если ранг м-цы совместной системы равен числу переменных, т.е. r=n, то система (2.1) имеет единственное решение.

2. Если ранг м-цы совместной системы меньше числа переменных, т.е. r<n, то система (2.1) неопределённая и имеет бесконечное множество решений.

Замечание. Отличный от нуля минор порядка r, где r<n, будем называть базисным минором. Неизвестные х₁, х₂, …, х_r так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной.

Если свободные неизвестные обозначить х_r+1=c₁, х_r+2=c₂, …, х_n=c_n-r, то базисные неизвестные будут от них зависеть, то есть решение системы m уравнений с n неизвестными будет иметь вид

X = (x₁(c₁, …, c_n-r), x₂(c₁, …, c_n-r), …, x_r(c₁, …, c_n-r), c₁, c₂, …, c_n-r)^T, где значок Т означает транспонирование.

Такое решение системы называется общим.