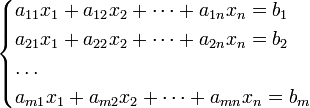- •2.Понятие определителя n-ого порядка. Схемы вычисления определителей 2-ого и 3-ого порядков
- •3.Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя.
- •4.Свойства определителей. Вычисление определителей порядка выше 3-его при помощи свойств определителя и теоремы о разложении определителя.
- •5.Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Алгоритм вычисления обратной матрицы.
- •6.Ранг матрицы. Преобразования матрицы, не меняющие ее ранга.
- •7.Системы m линейных уравнений с n неизвестными. Основные понятия. Матричный вид системы линейных уравнений.
- •8.Системы n линейных уравнений с n неизвестными. Метод обратной матрицы.
- •9.Системы линейных уравнений с n неизвестными.Формулы Крамера.
- •10.Метод Гаусса решения системы m линейных уравнений с n неизвестными.
- •12.Системы линейных однородных уравнений. Существование ненулевого решения.
- •15.Скалярное произведение векторов и его свойства.Условие перпендикулярности векторов.Угол между векторами.
- •16.Векторное произведение и его свойства.
- •17.Смешанное произведение и его свойства.Условие компланарности векторов.
- •18.Общее уравнение прямой на плоскости. Случаи расположения прямой относительно осей координат.Уравнение прямой в отрезках.
- •19.Уравнение прямой с угловым коэффициентом.Уравнение прямой, проходящей через данную точку в данном направлении.
- •20.Уравнение прямой, проходящей через две данные точки (на плоскости).
- •21.Угол между двумя прямыми (на плоскости). Условия параллельности и перпендикулярности прямых.
- •22.Расстояние от точки до прямой.
- •23.Эллипс
- •24.Гипербола.
- •25.Парабола.
- •26.Поворот и параллельный перенос осей координат (на плоскости).
- •28.Случаи расположения плоскости относительно осей координат.Уравнение плоскости в отрезках.
- •29.Условие параллельности и перпендикулярности плоскостей. Угол между плоскостями.
- •30.Уравнение прямой в пространстве,как линии пересечения двух плоскостей. Канонические уравнения прямой в пространстве.
- •31.Уравнения прямой в пространстве, проходящей через две данные точки. Параметрические уравнения прямой в пространстве.
- •33.Предел числовой последовательности.
- •34.Предел функции на бесконечности.
- •32.Угол между прямой и плоскостью
- •35.Предел функции в точке.
- •36.Бесконечно малые функции. Связь бесконечно малой функции и функции, имеющей предел.Свойства бесконечно малых функций.
- •37.Бесконечно большие функции.Их свойства.Теорема о связи бесконечно большой и бесконечно малой функций.
- •38.Теорема о единственности предела.Основные теоремы о пределах.Предел сложной функции.
- •Теорема о пределе сложной функции.
- •39.Признаки существования пределов.
- •Теорема о сохранении функцией знака своего предела
- •40.Первый замечательный предел.
- •41. Сравнение бесконечно малых функций. Примеры эквивалентных бесконечно малых функций.
- •42.Второй замечательный предел.Число е.Важные пределы как следствие второго замечательного предела.
- •43.Задача о непрерывном начислении процентов.
- •44.Непрерывность функции в точке.Приращение функции,приращение аргумента.Свойства функций, непрерывных в точке.
- •45.Непрерывность функции на отрезке.
- •46.Классификация точек разрыва.
- •47.Задача о скорости неравномерного прямолинейного движения.
- •48.Задача о касательной, приводящая к понятию о производной.
- •49.Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции. Примеры недифференцируемых функций в точке.
- •Замечание
- •54.Производная степенной функции. Логарифмическая производная.
- •55.Производные высших порядков.
6.Ранг матрицы. Преобразования матрицы, не меняющие ее ранга.
Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n-го порядка, определитель которой Δk называется минором k–го порядка матрицы A.
Рангом матрицы А называется наивысший порядок отличных от 0 миноров этой матрицы [rang A=r(A)]. Ранг матрицы не изменяется при проведении элементарных преобразований.
Преобразования
1)отбрасывание строки или столбца, состоящих из одних нулей
2)умножение всех эл-ов к.-л. строки или столбца матрицы на одно и то же число, отличное от 0;
3)изменение порядка строк или столбцов матрицы;
4)прибавление к каждому эл-ту к.-л. строки или столбца эл-ов др. строки или столбца, умноженных на одно и то же число, не равное 0;
5) транспонирование матрицы.
Теорема о ранге матрицы. Ранг м-цы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).
7.Системы m линейных уравнений с n неизвестными. Основные понятия. Матричный вид системы линейных уравнений.
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
(1) |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Cистема линейных уравнений может быть представлена в матричной форме как:
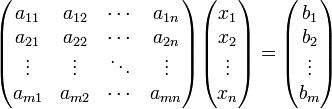
или:AX = B.Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. (A/B)
След. Преобразования над слу не приводят к изменениям его корней:
Изменение порядка уравнений в системе
Умножение уравнения на ненулевое число
+ и – из одной строки другой
+ и – из одной строки другой умноженной на ненулевое число