46. Классификация точек разрыв

Определение. Если ф-ция f(x) такова, что сущ. конечные пределы и , но либо ф-ция f(x) не определена в точке х₀, либо не все 3 числа f(x₀), f(x₀-0), f(x₀+0) = друг другу, то точка х₀ - точка разрыва 1 рода ф-ции f(x).

В частности, если пределы слева и справа в этой точке совпадают f(x₀-0)=f(x₀+0), но ф-ция в точке х₀ не определена, то точка х₀ называется устранимой точкой разрыва (её можно устранить, положив ; после чего, определенная т.о. ф-ция будет непрерывной)

Определение. Все точки разрыва, не являющиеся точками разрыва 1-го рода называются точками разрыва 2-го рода. К точкам разрыва 2-го рода относят точки ∞го разрыва.

Используя св-ва пределов можно док-ть следующие утверждения:

1. Сумма 2-ых непрерывных ф-ций – непрерыв. ф –ция;

2. Произведение 2-х непрерывных ф-ций – ф –ция непрерывная;

3. Частное 2-х непрерывных ф-ций – непрерыв. ф –ция, если знаменатель не обращается в 0.

4. Если ф-ция u=u(x) непрерывна в точке х₀, а ф-ция у=у(х) непрерывная в точке u₀=u(x₀), то сложная ф-ция y(u(x)) – непрерывная в точке х₀

Используя эти утверждения можно док-ть сл. теорему:

Всякая элементарная ф-ция непрерывна в любой точке, в кот. она определена.

47. Непрерывность функции на интервале и на отрезке

Определение. Если ф-ция y=f(x) непрерывна в каждой точке некот. интервала (а;b), то говорят, что она непрерывна на данном интервале (а;b).

Определение. Если ф-ция y=f(x) определена при х=х₀ и если сущ. предел ( ), то ф-ция f(x) наз. непрерывной в точке х₀ слева (справа).

Определение. Ф-ция f(x) наз. непрерывной на отрезке [a;b], если она непрерывна на интервале (а;b), а также она непрерывна в точке а справа, и в точке b слева.

48. Некот свойсва непрерывной ф-ции

Т-ма: Если ф-ция y=f(x) непрерывна на отрезке [a;b], то на этом отрезке найдется точка х=х₁ такая, что f(x)≤f(x₁) и точка х=х₂ такая, что f(x)≥f(x₂). Для всех др. значений х, принадлежащих отрезку [a;b], значения f(x₁) и f(x₂) наз. соответственно наибольшим и наименьшим значениями ф-ции f(x) на отрезке [a;b].

Иначе эту теорему можно сформулировать так: Функция непрерывная на отрезке, достигает своего наиб. и наим. значений.

1. а=х₂, b=x₁

2 . [-1,1] – не выполняется условие непрерывности.

3. y=x (0,1) – не выполняется условие непрерывности. Выполнилось бы на участке [0,1]

Т-ма: Пусть ф-ция y=f(x) непрерывна на отрезке [a;b] и принимает на концах этого отрезка значение разных знаков, тогда существует некот. точка С на этом отрезке, в кот. ф-ция обращается в 0. (f(c)=0)

Геометрически утверждение теоремы сводится к тому, что график такой ф-ции обязательно пересечет ось Ох хотя бы в одной точке.

53. Производная сложной ф-ции.

Пусть дана сложная ф-ция y=f(х), т.е y=y(u), где u=u(x), т.е y=y(u(x)), x-независимая переменная, u -промежуточный аргумент.

Теорема. Производная сложной ф-ции y=y(u(x)) = произведению производной ф-ции y по промежуточному аргументу U на производную от промежуточного аргумента по независимой переменной x т.е y_x’=y_u’∙U_x’.

Док-во. Пи определённом значении x u=u(x), y=y(u), при значении x=x+∆х, y+∆у=y(u+∆u), где u+ u=U(x+ x); По определению производной . Ф-ция отличается от своего предела на ∞ малое слагаемое т.е . Умножим обе части равенства на ∆U. Тогда . Разделим обе части равенства на ∆х и перейдем к пределу при ∆х→0.

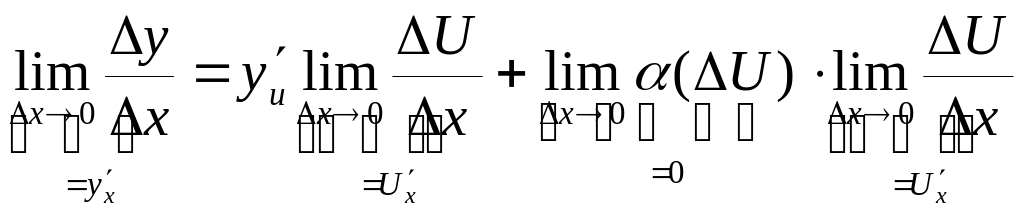
Т. к. ф-ция U(x) дифференцируема, то она непрерывна. Поэтому при ∆х→0 и ∆U→0. Поэтому

Таким образом, получим y_x’=y_u’∙U_x’. ч.т.д