- •1. Случайный эксперимент. Пространство исходов. Случайное событие.
- •2. Классическое определение вероятности. Свойства вероятности (из определения). Недостатки определения.
- •3. Основные формулы комбинаторики.
- •4. Геометрическое определение вероятности. Его недостатки. Задача Бюффона. Задача о встрече.
- •5. Частота события. Статистическое определение вероятности. Понятие устойчивости и законе больших чисел. Недостатки определения.
- •6. Алгебра событий. Аксиоматическое определение вероятности. Свойства вероятности из аксиоматического определения.
- •8. Условные вероятности. Теорема умножения вероятности, независимые события. Попарная независимость и независимость в совокупности.
- •9. Вероятность наступления хотя бы одного события.
- •10. Формула полной вероятности. Формула Байеса.
- •11. Схема Бернулли. Формула Бернулли.
- •12. Приближенные формулы для формулы Бернулли: локальная и интегральная формула Муавра-Лапласса. Формула Пуассона.
- •13. Отклонение относительной частоты от постоянной вероятности. Закон больших чисел в формуле Бернулли.
- •14. Случайные величины: дискретные и непрерывные
- •15. Закон распределения дискретной случайной величины. Многоугольник (полигон) распределения.
- •16. Неперывная случайная величина. Функция распределения, ее свойства. Плотность распределения, ее свойства.
- •17. Числовые характеристики случайных величин и их свойства.
- •19. Правило трех сигм
- •22. Эмпирическая функция распределения: полигон и гистограмма.
- •23. Числовые характеристики выборки.
- •28. Коэффициент корреляции. Его основные свойства и статистический смысл.
- •29. Задачи регрессионного анализа. Линейная регрессия.
17. Числовые характеристики случайных величин и их свойства.
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .
Математическое ожидание дискретной случайной величины x , имеющей распределение
x1 |
x2 |
... |
xn |
p1 |
p2 |
... |
pn |
называется
величина
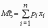 ,
если число значений случайной величины
конечно.
,
если число значений случайной величины
конечно.
Если
число значений случайной величины
счетно, то
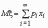 .
При этом, если ряд в правой части равенства
расходится, то говорят, что случайная
величина x не имеет математического
ожидания.
.
При этом, если ряд в правой части равенства
расходится, то говорят, что случайная
величина x не имеет математического
ожидания.
Математическое
ожидание непрерывной случайной величины
с плотностью вероятностей px
(x) вычисляется по формуле
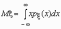 .
При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина x не имеет математического
ожидания.
.
При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина x не имеет математического
ожидания.
Если случайная величина h является функцией случайной величины x , h = f(x), то
 .
.
Аналогичные формулы справедливы для функций дискретной случайной величины:
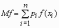 ,
,
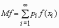 .
.
Основные свойства математического ожидания:
математическое ожидание константы равно этой константе, Mc=c ;
математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h );
математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).
Дисперсия случайной величины
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
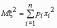 ,
,
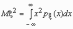 .
.
Для
определения меры разброса значений
случайной величины часто используется
среднеквадратичное отклонение
 ,
связанное с дисперсией соотношением
,
связанное с дисперсией соотношением
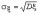 .
.
Основные свойства дисперсии:
дисперсия любой случайной величины неотрицательна, Dx
 0;
0;
дисперсия константы равна нулю, Dc=0;
для произвольной константы D(cx ) = c2D(x );
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).
18. Основные законы распределения случайных величин: Бернулли, биноминальный, Пуассона, гипергеометрический, равномерный, показательный и нормальный законы распределения. Критериальные распределения (хи-квадрат, т-Стьюдента, Ф- Фишера)
Распределение Пуассона
Распределение Пуассона и биномиальное распределение имеют некоторое сходство, но имеют и некоторые различия. Биномиальное распределение описывает распределение двух возможных исходов: "успеха" и "неудачи" в конечном числе n независимых испытаний. Распределение Пуассона сконцентрировано только на числе дискретных исходов на некотором интервале или континууме. Для него неважно число экспериментов n, как для биномиального распределения.
Распределение Пуассона описывает появление редких событий, и его еще называют законом "неправдоподобных" событий.
Распределение Пуассона имеет следующие характеристики:
- дискретное распределение;
- описывает редкие события;
- каждый исход является независимым от другого;
- описывает дискретные исходы на интервале или на континууме;
- исходы на каждом интервале могут быть проранжированы от нуля до бесконечности (случайная величина Х может принимать значения 0, 1, 2, ..., m,...;).
Распределение Пуассона определяется как
|
(1.41) |
Параметр a является средним для данного интервала, значение которого должно сохраняться для всего данного эксперимента.
Значение параметра a для закона Пуассона совпадает с дисперсией, и это используется для подтверждения того, что случайная величина распределена по закону Пуассона.
Распределение
Пуассона используется для аппроксимации
биномиального закона распределения
при
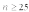 и
и
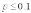 .
В этом случае a = np, где n -
число независимых экспериментов, p
- вероятность "успеха" в одном
эксперименте.
.
В этом случае a = np, где n -
число независимых экспериментов, p
- вероятность "успеха" в одном
эксперименте.
Учитывая это, вероятность m "успехов" в n испытаниях определяется в виде
|
(1.42) |
Примечание. Существует правило большого пальца, которое состоит в следующем. Если n > 20 и p < 0.1, то можно использовать распределение Пуассона вместо биномиального.
Пример. 2 % книг имеют дефект в переплете. Определить вероятность того, что 5 из 400 книг имеют дефект в переплете.
Решение. Так как и , то воспользуемся аппроксимацией биномиального закона законом Пуассона. Тогда a = np = 400·0.02, e–8 = 0.00034 (см. табл. V Приложения):
 .
.
В
общей форме биномиальный закон описывает
осуществление признака в
испытаниях
с возвратом. Наглядной схемой таких
испытаний является последовательный
выбор с возвращением шаров из урны,
содержащей
 белых
и
белых
и
 чёрных
шаров. Если
чёрных
шаров. Если
 —
число появления белых шаров в выборке
из
—
число появления белых шаров в выборке
из
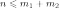 шаров, то
шаров, то
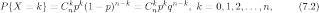 где
где
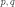 —
вероятность появления при одном
извлечении соответственно белого и
чёрного,
—
вероятность появления при одном
извлечении соответственно белого и
чёрного,

Производящая функция биномиального распределения задаётся формулой
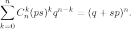
Основные характеристики биномиального распределения (математическое ожидание и дисперсия):

Равномерный закон распределения
Равномерное распределение задаётся следующим законом:
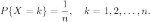
Этот
закон имеет место в случае, когда
возможных
исходов испытания равновероятны.
Примером целочисленной случайной
величины, распределённой по равномерному
закону, может служить число очков,
выпадающих при бросании симметричной
кости (любое из значений
 выпадает
с одинаковой вероятностью
выпадает
с одинаковой вероятностью
 ).
Характеристическая функция равномерного
закона задаётся формулой
).
Характеристическая функция равномерного
закона задаётся формулой
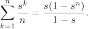
Числовые характеристики геометрического закона распределения (математическое ожидание и дисперсия):

Гипергеометрический закон распределения
Случайная
величина
имеет
гипергеометрическое распределение с
параметрами
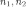 и
и
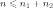 (
(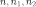 — натуральные числа), если она принимает
конечное множество натуральных значений
— натуральные числа), если она принимает
конечное множество натуральных значений
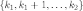 соответственно
с вероятностями
соответственно
с вероятностями
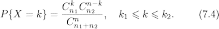
причём
 .
.
Гипергеометрическое
распределение возникает в экспериментах
по выбору без возвращения
шаров
из урны, содержащей
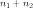 шаров,
из которых
шаров,
из которых
 белых
и
белых
и
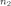 чёрных.
Таким образом, это распределение
описывает осуществление признака в
выборке без возврата (в отличии от
биномиального распределения). На практике
к гипергеометрическому распределению
приводят задачи, где изделия из партии
отбирают случайно (обеспечивая для
каждого изделия равную возможность
быть отобранным), но отобранные изделия
не возвращают в партию. Такой отбор
особенно важен в тех задачах, где проверка
изделия связана с его разрушением
(например, проверка изделия на срок
службы).
чёрных.
Таким образом, это распределение
описывает осуществление признака в
выборке без возврата (в отличии от
биномиального распределения). На практике
к гипергеометрическому распределению
приводят задачи, где изделия из партии
отбирают случайно (обеспечивая для
каждого изделия равную возможность
быть отобранным), но отобранные изделия
не возвращают в партию. Такой отбор
особенно важен в тех задачах, где проверка
изделия связана с его разрушением
(например, проверка изделия на срок
службы).
Числовые характеристики гипергеометрического распределения (математическое ожидание и дисперсия):
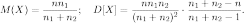
Следует заметить, что если очень велико по сравнению с , то не имеет существенного значения, возвращаются шары обратно или нет, и формула (7.4) может быть приближённо заменена формулой (7.1) биномиального распределения.
Нормальное распределение.
Говорят,
что случайная величина
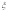 нормально
распределена или подчиняется закону
распределения Гаусса, если ее плотность
распределения
нормально
распределена или подчиняется закону
распределения Гаусса, если ее плотность
распределения
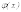 имеет
вид
имеет
вид
|
(28) |
где
a - любое действительное число, а
 >0.
Смысл параметров a и
будет
установлен в дальнейшем. Исходя из
связи между плотностью распределения
и
функцией распределения F(x) имеем
>0.
Смысл параметров a и
будет
установлен в дальнейшем. Исходя из
связи между плотностью распределения
и
функцией распределения F(x) имеем
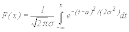
Показательное распределение (непрерывное)
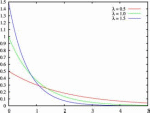
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.Плотность распределения:
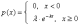 Где
Где
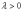 .
Числовые характеристики:
.
Числовые характеристики:
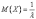 ,
,
 ,
,
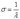
Плотность распределения при различных значениях .
Распределение хи-квадрат определяется следующим образом:
f(x)
= {1/[2 /2
*
/2
*
 (
/2)]}
* [x(
/2)-1
* e-x/2]
=
1, 2, ..., 0 < x
(
/2)]}
* [x(
/2)-1
* e-x/2]
=
1, 2, ..., 0 < x
где - число степеней свободы e - число Эйлера (2.71...) - гамма-функция
Распределение Фишера
Пусть
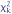 имеет
распределение
имеет
распределение
 ,
а — распределение
,
а — распределение
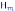 ,
причем эти случайные величины независимы.
Распределение случайной величины
,
причем эти случайные величины независимы.
Распределение случайной величины
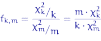
называют распределением Фишера с
 ,
,
 степенями
свободы и обозначают
степенями
свободы и обозначают
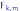 .
.
Свойства распределения Фишера (или Фишера — Снедекора):
1.
Если
 имеет
распределение Фишера
,
то
имеет
распределение Фишера
,
то
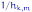 имеет
распределение Фишера
имеет
распределение Фишера
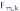 .
.
2. Распределение Фишера
слабо
сходится к вырожденному в точке 1
распределению
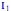 при
любом стремлении
и
к бесконечности.
при
любом стремлении
и
к бесконечности.
Доказательство. Убедитесь по ЗБЧ, что любая последовательность случайных величин , распределение которой совпадает с распределением отношения двух средних арифметических
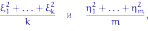
сходится
к 1 по вероятности при
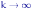 ,
,
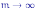 .
Здесь
.
Здесь
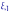 ,
,
 ,
,
 и
и
 ,
,
 ,
—
независимые последовательности,
составленные из независимых случайных
величин со стандартным нормальным
распределением.
,
—
независимые последовательности,
составленные из независимых случайных
величин со стандартным нормальным
распределением.
Распределение Стьюдента Другое название – T-распределение
Обозначение |
|
Область значений |
|
Параметры |
Параметр формы
положительное число |
Плотность (функция вероятности) |
|
Математическое ожидание |
0 |
Дисперсия |
|
Функция распределения |
Не выражается в элементарных функциях |

 .
.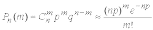 .
.
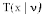
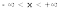
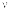 ,
число степеней свободы, целое
,
число степеней свободы, целое
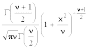
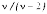 ,
,