3. Основные формулы комбинаторики.

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!, где n! = 1 * 2 * 3 ... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений A^m_n = n (n - 1)(n - 2) ... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

С ^m_n = n! / (m! (n - m)!).

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

A^m_n = P_mC ^m_n.

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂, ...) = n! / (n₁! n₂! ... ), где n₁ + n₂ + ... = n.

При решении задач комбинаторики используют следующие правила:

П р а в и л о   с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

П р а в и л о   п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

4. Геометрическое определение вероятности. Его недостатки. Задача Бюффона. Задача о встрече.

Предположим, что два человека условились о встрече в некотором месте между девятью и десятью часами. Они договорились, что каждый ждет другого в течение четверти часа, а затем уходит. Какова вероятность, что они встретятся? Пусть x - момент прихода одного человека на место встречи, а y - момент прихода другого человека. Точку на плоскости с координатами (x;y) будем рассматривать как один из исходов встречи. Все возможные исходы лежат в площади квадрата, сторона которого соответствует промежутку времени длительности в один час. Исход будет благоприятным (встреча состоится), если точка (x;y) такова, что ¦x;y¦<1/4. Такие точки лежат в пределах заштрихованного участка площади квадрата. Все исходы равновозможны и несовместны, поэтому вероятность встречи равна отношению заштрихованной площади ко всей площади квадрата.

Площадь благоприятной области равна разности площадей всего квадрата и его не заштрихованной части 1-(3/4)*2=7/16, значит вероятность встречи: 7/16.

Рассмотренный пример иллюстрирует геометрическое определение вероятности: вероятность случайного события есть отношение площади области, благоприятствующей появлению события, к площади всей области. Геометрическое определение вероятности является обобщением классического определения на случай, когда число равновозможных исходов бесконечно.

Вероятность события А определяется формулой

Ж. Бюффон рассматривал следующую ситуацию: на плоскость, разграфленную параллельными прямыми, отстоящими друг от друга на расстоянии а, наудачу бросается игла длиною 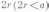. Какова вероятность того, что игла пересечет одну из проведенных параллелей? Очевидно, что положение иглы определяется расстоянием хот ее центра до ближайшей прямой линии и острым углом 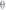, составленным иглой с перпендикуляром к этой линии. 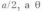Величина хлежит между нулем и - между нулем и 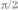. Предполагается, что точка 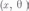распределена равномерно в соответствующем прямоугольнике (это равносильно тому, что случайные величины хи 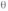независимы и равномерно распределены на 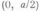и ). Тогда искомая вероятность определяется как отношение площадей, соответствующих благоприятствующим и всем возможным исходам, и равна