15. Закон распределения дискретной случайной величины. Многоугольник (полигон) распределения.

На первый взгляд может показаться, что для задания дискретной случайной величины достаточно пере­числить все ее возможные значения. В действительности -это не так: случайные величины могут иметь одинако­вые перечни возможных значений, а вероятности их появления — различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

 Заданное соответствие между возможными значениями ДСВХ и их вероятностями называется законом распределения дискретной случайной величины ; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:

Х	x1	x2	…	xn
р	p1	p2	…	pn

Эта таблица называется рядом распределения.

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное зна­чение, заключаем, что события Х=х₁, Х=х₂, …, Х=х_n - образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

 

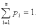
Если множество возможных значений Х бесконечно (счетно), то ряд

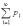
сходится и его сумма равна единице.

Пример1.  В партии из восьми деталей пять стандартных, наудачу взяты четыре детали. Построить ряд распределения числа стандартных деталей среди отобранных.

 Пусть Х—число стандартных деталей среди четырех отобранных. Оно может принять следующие четыре значения: х₁=1, х₂=2, х₃=3, х₄=4. Вычислим вероятность появления каждого из них:

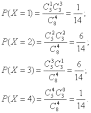
Проверим вычисления. Складывая полученные вероятности, получим: 1/14+ 6/14+ 6/14 + 1/14=1. Искомый ряд распределения данной ДСВХ имеет вид:

Х	1	2	3	4
р	1/14	6/14	6/14	1/14

Ряд распределения можно представить графически, если по оси абсцисс отложить возможные значения ДСВХ, а по оси ординат - соответствующие вероятности. Соединив полученные точки отрезками, получим ломаную, называемую многоугольником распределения вероятностей.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

            Графическое представление этой таблицы называется многоугольником распределения.  При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

16. Неперывная случайная величина. Функция распределения, ее свойства. Плотность распределения, ее свойства.

Случайная   величина , значения которой заполняют некоторый промежуток, называется  непрерывной .

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу­бесконечными или бесконечными, например: (a; b], (– ; a), [b;), (–; ).

Пусть  –  непрерывная   случайная   величина . Функция F(x), которая определяется равенством

,

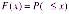называется интегральной функцией распределения или просто функцией распределения  случайной   величины  . Непосредственно из определения следует равенство 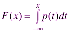. Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению 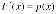. Плотность распределения р(х) называют дифференциальной функцией распределения.

Функция распределения F(x)  случайной   величины   имеет следующие свойства.

1. F(x) —  непрерывная  возрастающая функция.

2. ;

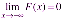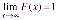
Свойства 1 и 2 вытекают непосредственно из определения функции F(x).

3. Приращение F(x) на промежутке (х₁; х₂) равно вероятности того, что  случайная   величина   принимает значение из этого промежутка:

F(x₂) – F(x₁) = P(x₁ <   x₂)

Доказательство.

F(x₂) = P(  x₂) = P(  x₁) + P(x₁ <   x₂) = F(x₁) + P(x₁ <   x₂)

Отсюда

P(x₁ <   x₂) = F(x₂) – F(x₁)

Заметим, что для  непрерывной   случайной   величины   справедливы равенства

P(x₁ <   x₂) = P(x₁ <  < x₂) = P(x₁   < x₂) = P(x₁    x₂)

Для равномерного распределения функция F(x) имеет вид:

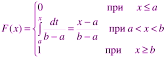
Рис. 3

График функции F(x) представлен на рисунке 3.

Закон распределения  непрерывной   случайной   величины  можно определить заданием либо функции р(х), либо функции F(x).

Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения:  р(Х = а) = F(a) – F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.

Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифферен-циальная функция).

Определение 5.1. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле:

                                                         f (x) = F′(x),                                                          

то есть является производной функции распределения.

                     Свойства плотности распределения.

1)      f(x) ≥ 0, так как функция распределения является неубывающей.

2)      , что следует из определения плотности распределения.

3) Вероятность попадания случайной величины в интервал (а, b) определяется формулой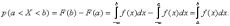            

4) 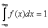      (условие нормировки). Его справедливость следует из того, что 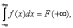 а

5)       так как 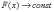 при

Таким образом, график плотности распределения представляет собой кривую, располо-женную выше оси Ох, причем эта ось является ее горизонтальной асимптотой при 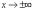 (последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице.

Замечание. Если все возможные значения непрерывной случайной величины сосредоточены на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала   [a, b]  f(x) ≡ 0.