11. Схема Бернулли. Формула Бернулли.

Повторные независимые испытания

На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие . При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа появлений события в результате испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события в каждом испытании постоянна. Такие испытания называются повторными независимыми.

Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

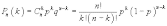
В формуле Бернулли используется число сочетаний. для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const (постоянное значение вероятности появления события) Распределение вероятностей в схеме Бернулли - биномиальное. Наивероятнейшее число появления события (мода) при n испытаниях заключено в пределах np-q ≤ Mo ≤ np+p,

12. Приближенные формулы для формулы Бернулли: локальная и интегральная формула Муавра-Лапласса. Формула Пуассона.

Локальная и интегральная теоремы Лапласа

В схеме Бернулли (см. предыдущий пункт) распределение вероятностей - биномиальное. При большом количестве проводимых испытаний биномиальное распределение приближается к нормальному с параметрами a = np, σ = √(npq). На этом факте и основано применение приближённых формул Лапласа. Условия применения формул - схема Бернулли (проводимые испытания независимы, вероятность наступления события в каждом испытании постоянна). Тогда вероятность того, что при n испытаниях интересующее нас событие наступит ровно k раз (безразлично, в какой последовательности), приближённо равна

Чем больше n, тем ближе значение вероятности к точному. Значения функции можно вычислить с помощью инженерного калькулятора. Если есть под рукой таблица значений функции плотности стандартного нормального распределения 1/√2π·e^(-x2/2), то сначала вычисляем величину x = (k-np)/√npq, а потом смотрим нужное значение. Можно также воспользоваться функцией Excel =НОРМРАСП(k;np; √npq;0)

Пример 8.1

Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

Показать решение

Решение Здесь имеется схема Бернулли. Так как количество испытаний велико, вместо формулы Бернулли воспользуемся приближённой формулой Лапласа. k = 75; np = 0,8·100 = 80; √npq = √0,8·100·0,2 = √16 = 4 НОРМРАСП(75; 80; 4; 0) = 0,0457 Свернуть

Если же при прежних условиях требуется найти вероятность того, что событие наступит не менее k₁ и не более k₂ раз, то используется интегральная формула Лапласа.

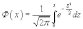- функция Лапласа. Значения функции Лапласа можно взять из таблицы. Можно также воспользоваться программой Excel. Функция =НОРМСТРАСП() позволяет вычислить интегральную функцию нормального распеделения F(X). Взаимосвязь между интегральной функцией и функцией Лапласа: Ф(X) = F(X) - 0,5. Поэтому для вычисления функции Лапласа в ячейку забиваем формулу =НОРМСТРАСП(число) - 0,5 Функция Лапласа нечетная, т.е. Ф(-X) = -Ф(X). Это к сведению для тех, кто будет пользоваться таблицей значений функции Лапласа (там, как правило, отсутствуют отрицательные значения аргумента).

Пример 8.2

Найти вероятность того, что число выпадений на игральной кости числа 4 при 1000 бросаниях будет заключено между числами 161 и 171.

Решение Игральная кость (кубик) имеет шесть граней, на каждой из которых имеется определённое количество очков (от 1 до 6). При каждом отдельном бросании вероятность выпадения четырёх очков постоянна и равна 1/6. Проводимые испытания независимы. Следовательно, в задаче имеется схема Бернулли. Но формула Бернулли в данном случае даёт громоздкие вычисления, т.к. количество испытаний очень большое. При больших n биномиальное распределение приближается к нормальному, поэтому вероятность можно вычислить приближённо, используя интегральную формулу Лапласа:

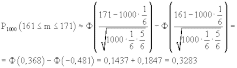
Свернуть

Приближённая формула Пуассона

Если при наличии схемы Бернулли число испытаний n велико, а вероятность наступления события p мала, то вместо формулы Бернулли используют формулу Пуассона:

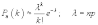
Здесь вы можете найти таблицу распределения Пуассона. В Excel значения можно вычислить по формуле =ПУАССОН(k;λ;0)

Пример 9.1

Вероятность выпуска бракованного сверла (повышенной хрупкости) равна 0,02. Свёрла укладывают в коробки по 100 штук. Определить вероятность того, что число бракованных свёрл коробке не превосходит трёх.